Giải Câu 41 Bài 6: Tính chất ba đường phân giác của tam giác sgk Toán 7 tập 2 Trang 73

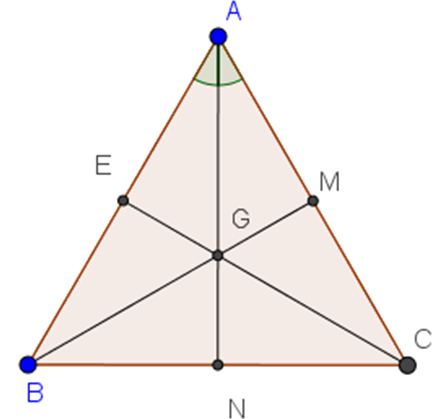
Giả sử ∆ABC đều có trọng tâm G, các trung tuyến AN, BM, CE.

$\Rightarrow GA = \frac{2}{3},AN; GB = \frac{2}{3}.BM; GC = \frac{2}{3}.EC$ (tính chất đường trung tuyến trong tam giác)

Vì ∆ABC đều nên ba trung tuyến AN, BM, CE bằng nhau.

$\Rightarrow GA = GB = GC$ (vì cùng = $\frac{2}{3}$ các đoạn bằng nhau)

Xét $∆AMG$ và $ ∆CMG$ có:

$GM$ chung

$AM =MC$ (M là trung điểm AC)

$AG =CG$ (cmt)

$\Rightarrow \Delta AMG = \Delta CMG\,\ (c.c.c)$

$\Rightarrow \widehat{AMG}=\widehat{CMG}$

Mà \(\widehat{AMG}+\widehat{CMG}= 180^0\)

$\Rightarrow \widehat{AMG}=  90^0$

$\Rightarrow GM ⊥ AC$ tức là GM khoảng cách từ G đến AC.

Chứng minh tương tự GE, GN là khoảng cách từ G đến AB, BC.

Mà $GM =\frac{1}{3}.BM; GN = \frac{1}{3}.AN; EG = \frac{1}{3}.EC$

Và $AN = BM = EC$ nên $GM = GN = GE$.

Hay G cách đều ba cạnh của tam giác ABC.