I. TRƯỜNG HỢP BẰNG NHAU GÓC - CẠNH - GÓC (G.C.G)

Hoạt động 1: Cho tam giác ABC (hình 56). Những góc nào của tam giác ABC có cạnh thuộc đường thẳng AB? 

Hướng dẫn giải:

Góc A và góc B của tam giác ABC có cạnh thuộc đường thẳng AB.

Hoạt động 2: Cho hai tam giác ABC và A'B'C' có: $\widehat{A}=\widehat{A'}=60^{0}$, AB = A'B' = 3cm, $\widehat{B}=\widehat{B'}=45^{0}$. Bằng cách đếm số ô vuông, hãy so sánh BC và B'C'. Từ đó có thể kết luận được hai tam giác ABC và A'B'C' hay không?

Hướng dẫn giải:

Tam giác ABC và tam giác A'B'C' bằng nhau.

Luyện tập 1: Cho hai tam giác ABC và A'B'C' thỏa mãn BC = B'C'=3cm, $\widehat{B} = \widehat{B'} = 60^{0}$, $\widehat{C} = 50^{0}$, $\widehat{A'} = 70^{0}$. Hai tam giác ABC và A'B'C' có bằng nhau không? Vì sao?

Hướng dẫn giải:

Hai tam giác ABC và A'B'C' bằng nhau vì có:

$\widehat{B}=\widehat{B'}$

BC = B'C'

$\widehat{C}=\widehat{C'}=50^{0}$ 

Luyện tập 2: Giải thích cho bài toán ở phần mở đầu

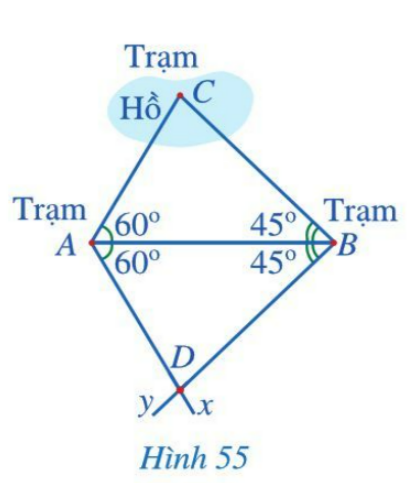
Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ. Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được các khoảng cách trên nên người ta làm như sau:

- Đo góc BAC được $60^{0}$, đo góc ABC được $45^{0}$

- Kẻ tia Ax sao cho $\widehat{BAx}=60^{0}$, kẻ tia By sao cho $\widehat{ABy}=45^{0}$, xác định giao điểm D của hai tia đó.

- Đo khoảng cách AD và BD. Ta có AC=AD và BC=BD.

Tại sao lại có hai đẳng thức trên?

Hướng dẫn giải:

Xét $\Delta ABC$ và $\Delta ABD$ có: 

AB chung

$\widehat{BAC}=\widehat{BAx}=60^{0}$

$\widehat{ABC}=\widehat{ABy}=45^{0}$

=> $\Delta ABC$ và $\Delta ABD$ (góc - cạnh - góc)

=> AC = AD, BC = BD