KHỞI ĐỘNG

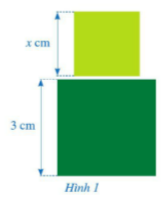
Câu hỏi: Trong giờ học môn Mĩ thuật bạn Hạnh dán lên trang của hai hình vuông có kích thước lần lượt là 3 cm và x như ở hình 1 tổng diện tích hai hình vuông đó là $x^{2}$ + 9 ($cm^{2}$). Biểu thức đại số $x^{2}$ + 9 có gì đặc biệt?

Hướng dẫn giải:

Biểu thức đại số $x^{2}$ + 9 là đa thức một biến.

I. ĐƠN THỨC MỘT BIẾN. ĐA THỨC MỘT BIẾN

Hoạt động 1: 

a. Viết biểu thức biểu thị: 

- Diện tích của hình vuông có độ dài cạnh là x cm

- Thể tích của hình lập phương có độ dài cạnh là 2x cm

b. Các biểu thức trên có dạng như thế nào?

Hướng dẫn giải:

a. Biểu thức biểu thị:

- Diện tích của hình vuông có độ dài cạnh là $x^{2}$

- Thể tích của hình lập phương có độ dài cạnh là a. $(2x)^{3}$

b. Các biểu thức trên có dạng đơn thức một biến.

Hoạt động 2: 

a. Viết biểu thức biểu thị:

- Quãng đường ô tô đi được trong thời gian x (h), nếu vận tốc của ô tô là 60km/h

- Tổng diện tích của các hình: hình vuông có độ dài cạnh là 2x cm; hình chữ nhật có các kích thước là 3cm và x cm; hình thoi có độ dài đường chéo là 4 cm và 8 cm

b. Các biểu thức trên có bao nhiêu biến? Mỗi số hạng xuất hiện trong biểu thức có dạng như thế nào?

Hướng dẫn giải:

a. Biểu thức biểu thị:

- Quãng đường ô tô đi được: S = 60 . x

- Tổng diện tích của các hình: hình vuông có độ dài cạnh là 2x cm; hình chữ nhật có các kích thước là 3cm và x cm; hình thoi có độ dài đường chéo là 4 cm và 8 cm: $2x^{2} + 3x + \frac{4 . 8}{2}$

b. Biểu thức trên có dạng đa thức một biến.

Luyện tập 1: Biểu thức nào sau đây là đa thức một biến? 

a. $x^{2}+9$

b. $\frac{2}{x^{2}} + 2x + 1$

c. $3x + \frac{2}{5}y$

Hướng dẫn giải:

Biểu thức $x^{2}+9$ và $\frac{2}{x^{2}} + 2x + 1$ là đa thức một biến.

Hoạt động 3: Cho hai đơn thức của cùng biến x là $2x^{2}$ và $3x^{2}$

a. So sánh số mũ của biến x trong hai đơn thức trên.

b. Thực hiện phép cộng $2x^{2} + 3x^{2}$ và $(2 + 3)x^{2}$

c. So sánh kết quả 2 phép tính

Hướng dẫn giải:

a. Số mũ của biến x trong hai đơn thức bằng nhau

b. $2x^{2} + 3x^{2} = 5x^{2}$

c. $2x^{2} + 3x^{2}$ = $(2 + 3)x^{2}$

Luyện tập 2:Thực hiện mỗi phép tính sau:

a. $x^{2} + \frac{1}{4}x^{2} - 5x^{2}$

b. $y^{4} + 6y^{4} - \frac{2}{5}y^{4}$

Hướng dẫn giải:

a. $x^{2} + \frac{1}{4}x^{2} - 5x^{2} = (1 + \frac{1}{4} - 5). x^{2} = (\frac{4+1-20}{4}).x^{2} =\frac{-15}{4}x^{2}$

b. $y^{4} + 6y^{4} - \frac{2}{5}y^{4} = (1+ 6 + \frac{2}{5})y^{4} = (\frac{5+30-2}{5}).y^{4} = \frac{33}{5}y^{4}$

 III. SẮP XẾP ĐA THỨC MỘT BIẾN

Hoạt động 4: Cho đa thức P(x) = $2x^{2} + 2x^{2} + 6x + 2x -3$

a. Nêu các đơn thức của biến x có trong đa thức P(x)

b. Tìm số mũ của biến x trong từng đơn thức nói trên

c. Thực hiện phép cộng các đơn thức có cùng số mũ của biến x sao cho trong đa thức P(x) không còn hai đơn thức nào có cùng số mũ của biến x.

Hướng dẫn giải:

a. Các đơn thức của biến x: $2x^{2}$; $2x^{2}$; 6x; 2x

b. Số mũ của biến x trong từng đơn thức:

$2x^{2}$: mũ 2

$2x^{2}$: mũ 2

6x: mũ 1

2x: mũ 1

c. P(x) = $2x^{2} + 2x^{2} + 6x + 2x -3$ = $4x^{2} + 8x -3$

Luyện tập 3: Thu gọn đa thức: 

P(y) = $-2y^{3} + y + \frac{11}{7}y^{3} + 3y^{2} - 5 - 6y^{2} + 9$ 

Hướng dẫn giải:

P(y)= $(-2y^{3} + \frac{11}{7}y^{3}) + (3y^{2} - 6y^{2}) + y - 5 + 9$

= $\frac{-28+22}{14}y^{3} - 3y^{2} + y + 4$

= $\frac{-6}{14}y^{3} - 3y^{2} + y + 4$

= $\frac{-3}{7} - 3y^{2} + y + 4$

Hoạt động 5: Cho đa thức R(x) = $-2x^{2} + 3x^{2} + 6x + 8x^{4} -1$

a. Thu gọn đa thức R(x)

b. Trong dạng thu gọn của đa thức R(x), sắp xếp các đơn thức theo số mũ giảm dần của biến.

Hướng dẫn giải: 

a) R(x)= $-2x^{2} + 3x^{2} + 6x + 8x^{4} -1$

= $(-2+3)x^{2} + 6x + 8x^{4} -1$

= $x^{2} + 6x + 8x^{4} -1$

b) R(x)= $8x^{4} + x^{2} + 6x - 1$

Luyện tập 4: Sắp xếp đa thức H(x) = $-0,5x^{8} + 4x^{3} + 5x^{10} -1$ theo:

a) Số mũ giảm dần của biến

b) Số mũ tăng dần của biến

Hướng dẫn giải:

a) H(x) = $5x^{10} - 0,5x^{8} + 4x^{3} - 1$

b) H(x) = $-1 + 4x^{3} - 0,5x^{8} +5x^{10}$

IV. BẬC CỦA ĐA THỨC MỘT BIẾN

Hoạt động 6: Cho đa thức P(x) = $9x^{4} + 8x^{3} - 6x^{2} + x - 1 - 9x^{4}$

a) Thu gọn đa thức P(x)

b) Tìm số mũ cao nhất của x trong dạng thu gọn của P(x)

Hướng dẫn giải:

a) P(x) = $9x^{4} + 8x^{3} - 6x^{2} + x - 1 - 9x^{4}$

= $8x^{3} - 6x^{2} + x - 1$

b) Số mũ cao nhất của x là 3

Luyện tập 5: Cho đa thức: R(x) = $-1975x^{3} + 1945x^{4} + 2021x^{5} - 4,5$

a) Sắp xếp đa thức R(x) theo số mũ giảm dần của biến

b) Tìm bậc của đa thức R(x)

c) Tìm hệ số cao nhất và hệ số tự do của đa thức R(x)

Hướng dẫn giải:

a) R(x) = $2021x^{5} + 1946x^{4} - 1975x^{3} - 4,5$

b) Đa thức R(x) bậc 5

c) Hệ số cao nhất: 2021

Hệ số tự do: -4,5

V. NGHIỆM CỦA ĐA THỨC MỘT BIẾN

Hoạt động 7: 

a) Tính giá trị của biểu thức đại số 3x - 2 tại x = 2

b) Tính giá trị của đa thức P(x) = -4x + 6 tại x = -3

Hướng dẫn giải:

a) Tại x=2, ta có: 3.2 - 2 = 4

b) Tại x - -3, ta có P(x) = (-4). (-3) + 6 = 18

Hoạt động 8: Cho đa thức P(x) = $x^{2} - 3x + 2$. Tính P(1), P(2)

Hướng dẫn giải:

Khi P(1), ta có: $1^{2} - 3.1 + 2$ = 1 - 3 + 2 = 0

Khi P(2), ta có: $2^{2} - 3.2 + 2$ = 4 - 6 + 2 = 0

Luyện tập 6: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) x = 4 và x = -4 là nghiệm của đa thức P(x) = $x^{2} - 16$

b) y = -2 là nghiệm của đa thức Q(y) = $-2y^{3} + 4$

Hướng dẫn giải:

a) P(x) = $x^{2} - 16$

Khi x = 4 => P(4) = $4^{2} - 16$ = 16 - 16 = 0

Khi x = -4 => P(-4) = $(-4)^{2} - 16$ = 16 - 16 = 0

Phát biểu a đúng.

b) Q(y) = $-2y^{3} + 4$

Khi y = -2 => Q(-2) = $-2.(-2)^{3} + 4$ = -2.(-8) + 4 = 16 + 4 = 20

Phát biểu b sai.