1. CỘNG HAI ĐA THỨC MỘT BIẾN

Luyện tập 1: Cho hai đa thức

  $M = 0,5x^4 – 4x^3 + 2x – 2,5$

  $N = 2x^3 + x^2 + 1,5$

Hãy tính tổng $M + N$ (trình bày theo 2 cách).

Hướng dẫn giải:

* Cách 1: Nhóm các hạng tử:

$M + N = 0,5x^4 – 4x^3 + 2x – 2,5 + (2x^3 + x^2 + 1,5)$

            $= 0,5x^4 – 4x^3 + 2x – 2,5 + 2x^3 + x^2 + 1,5$

            $= 0,5x^4 + (– 4x^3 + 2x^3) + x^2 + 2x + (-2,5 + 1,5)$

            $= 0,5x^4 – 2x^3 + x^2 + 2x + 1$

* Cách 2: Đặt tính cộng:

Vận dụng 1: Đặt tính cộng để tìm tổng của ba đa thức sau:

 $A = 2x^3 – 5x^2 + x -7$;

 $B = x^2 – 2x + 6$

 $C = -x^3 + 4x^2 – 1$.

Hướng dẫn giải:

2. TRỪ HAI ĐA THỨC MỘT BIẾN

Hoạt động 1: Tìm hiệu P - Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.

Hướng dẫn giải:

$P – Q = (x^4 + 3x^3 – 5x^2 + 7x) – (-x^3 + 4x^2 – 2x + 1)$

          $= x^4 + 3x^3 – 5x^2 + 7x + x^3 - 4x^2 + 2x - 1$

          $= x^4 + (3x^3 + x^3) + (-5x^2 – 4x^2) + (7x + 2x) – 1$ 

          $= x^4 + 4x^3 – 9x^2 + 9x - 1$

Hoạt động 2: Tìm hiệu P - Q bằng cách đặt tính trừ: đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột.

Hướng dẫn giải:

Đặt tính:

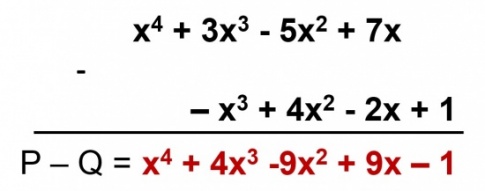
Luyện tập 2: Cho hai đa thức:

 $M = 0,5x^4 – 4x^3 + 2x – 2,5$

 $N = 2x^3 + x^2 + 1,5$

Hãy tính hiệu $M - N$ (trình bày theo 2 cách).

Hướng dẫn giải:

* Cách 1: Nhóm các hạng tử:

 $M + N = 0,5x^4 – 4x^3 + 2x – 2,5 - (2x^3 + x^2 + 1,5)$

            $= 0,5x^4 – 4x^3 + 2x – 2,5 - 2x^3 - x^2 - 1,5$

            $= 0,5x^4 + (– 4x^3 - 2x^3) - x^2 + 2x + (-2,5 - 1,5)$

            $= 0,5x^4 – 6x^3 - x^2 + 2x – 4 $

* Cách 2: Đặt tính cộng:

Vận dụng 2: Cho đa thức A = $x^4 – 3x^2 – 2x + 1$. Tìm các đa thức B và C sao cho:

 $A + B = 2x^5 + 5x^3 – 2$

 $A – C = x^3$ 

Hướng dẫn giải:

$B = A - 2x^5 + 5x^3 – 2$

   $= x^4 – 3x^2 – 2x + 1 – (2x^5 + 5x^3 – 2)$

   $= x^4 – 3x^2 – 2x + 1 – 2x^5 – 5x^3 + 2$

   $= -2x^5 + x^4 – 5x^3 - 3x^2 – 2x + (1 + 2)$

   $= -2x^5 + x^4 – 5x^3 - 3x^2 – 2x + 3$

$C = A - x^3$

    $= x^4 – 3x^2 – 2x + 1 - x^3$

    $= x^4 – x^3 – 3x^2 – 2x + 1$