Giải Bài 9: Tính chất ba đường cao của tam giác sgk Toán 7 tập 2 Trang 81
Hôm nay, chúng ta cùng tìm hiểu bài học "Tính chất ba đường cao của tam giác", thuộc phần hình 7. Dựa vào cấu trúc SGK, Tech12h tóm tắt kiến thức cần nhớ và hướng dẫn giải các bài tập một cách cụ thể, dễ hiểu. Hi vọng rằng đây là tài liệu có ích cho việc học tập của các em.

A. TÓM TẮT KIẾN THỨC
1. Định nghĩa
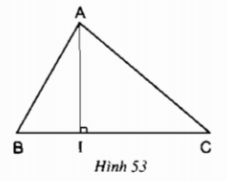
Đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.
Mỗi tam giác có ba đường cao.
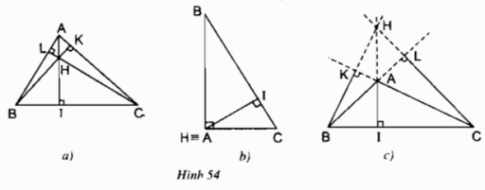
2. Tính chất ba đường cao của tam giác
Định lí
Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác
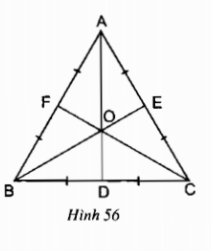
3. Vẽ đường cao, trung tuyến, trung trực, phân giác của tam giác cân
Định lí 1
Trong một tam giác cân, đường trung trực ứng với cạnh đáy cũng đồng thời là đường phân giác, đường trung tuyến và đường cao của tam giác đó.
Định lí 2
Trong một tam giác, nếu có một đường trung tuyến đồng thời là phân giác thì tam giác đó là tam giác cân.
Định lí 3
Trong một tam giác, nếu có một đường trung tuyến đồng thời là đường trung trực thì tam giác là tam giác cân.
4. Chú ý
Hệ quả:
Trong một tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau.

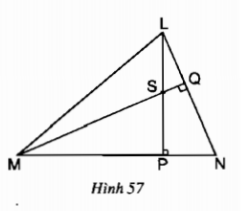
Bình luận