Giải bài 3 Tam giác cân
Giải bài 3 Tam giác cân - sách chân trời sáng tạo toán 7 tập 2. Phần đáp án chuẩn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức bài học.
1. Tam giác cân
Hoạt động khám phá 1: Gấp đôi một tờ giấy hình chữ nhật ABCD theo đường gấp MS. Cắt hình gấp được theo đường chéo AS rồi trải phẳng hình cắt được ra ta có tam giác SAB (Hình 1). Em hãy so sánh hai cạnh SA và SB của tam giác này.

 Hướng dẫn giải:
Hướng dẫn giải:
SA = SB.
Thực hành 1: Tìm các tam giác cân trong Hình 4. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của mỗi tam giác cân đó.

Hướng dẫn giải:
| Tam giác cân | Cạnh bên | Cạnh đáy | Góc ở đỉnh | Góc ở đáy |
| $\Delta MHP$ | MP = MH | HP | $\widehat{HMP}$ | $\widehat{MPH}$, $\widehat{MHP}$. |
| $\Delta MEF$ | ME = MF | EF | $\widehat{EMF}$ | $\widehat{MEF}$, $\widehat{MFE}$. |
| $\Delta MNP$ | MN = MP | NP | $\widehat{NMP}$ | $\widehat{MNP}$, $\widehat{MPN}$. |
2. Tính chất của tam giác cân
Hoạt động khám phá 2: Cho tam giác cân ABC cân tại A (Hình 5). Gọi M là trung điểm cạnh BC. Nối A với M. Em hãy làm theo gợi ý sau để chứng minh $\widehat{ABC} = \widehat{ACB}$
Xét $\Delta AMB$ và $\Delta AMC$ có:
AB = ? (?)
MB = MC (?)
AM là cạnh ?
Vậy $\Delta AMB = \Delta AMC$ (c.c.c).
Suy ra $\widehat{ABC} = \widehat{ACB}$.
Hướng dẫn giải:
Xét $\Delta AMB$ và $\Delta AMC$ có:
AB = AC
MB = MC
AM là cạnh góc vuông
Vậy $\Delta AMB = \Delta AMC$ (c.c.c).
Suy ra $\widehat{ABC} = \widehat{ACB}$.
Thực hành 2: Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.
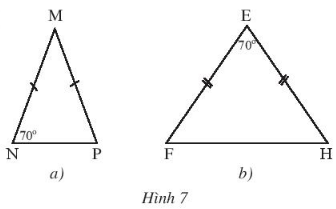
Hướng dẫn giải:
Tam giác MNP có MN = MP nên $\Delta MNP$ cân tại M.
$\Rightarrow $ $\widehat{N} = \widehat{P} = 70^{0}$
$\Rightarrow $ $\widehat{M} = 180^{0} - 70^{0} - 70^{0} = 40^{0}$
b. Tam giác EFH có EF = FH nên $\Delta EFH$ cân tại E.
$\Rightarrow $ $\widehat{F} = \widehat{H} = (180^{0} - 70^{0}) : 2 = 55^{0}$.
Vận dụng 1: Trong hình mái nhà ở Hình 8, tính góc B và góc C, biết $\widehat{A}=110^{o}$.

Hướng dẫn giải:
Tam giác ABC có AB = AC nên $\Delta ABC$ cân tại A.
$\Rightarrow $ $\widehat{B} = \widehat{C} = (180^{0} - 110^{0}) : 2 = 35^{0}$.
Hoạt động khám phá 3: Cho tam giác ABC có $\widehat{A} = \widehat{C}$. Vẽ đường thẳng đi qua điểm B, vuông góc với AC và cắt AC tại H (Hình 9). Em hãy làm theo gợi ý sau để chứng minh BA = BC.
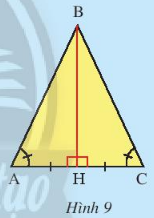
Hướng dẫn giải:
Xét $\Delta AHB$ và $\Delta CHB$ cùng vuông tại H, ta có:
BH là cạnh góc vuông
$\widehat{HAB} = \widehat{HCB}$ suy ra $\widehat{ABH} = \widehat{CBH}$ (vì $\widehat{ABH} = 90^{o} - $\widehat{HAB}$ và $\widehat{CBH}= 90^{o} - $\widehat{HCB}$.
Vậy $\Delta AHB = \Delta CHB$. Suy ra BA = BC.
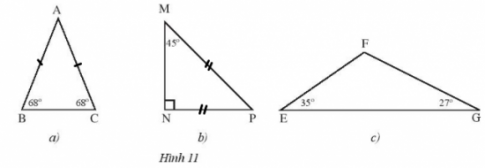
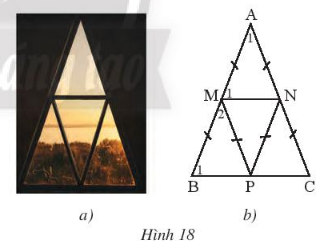
Thực hành 3: Tìm các tam giác cân trong Hình 11 và đánh dấu các cạnh bằng nhau.

Hướng dẫn giải:
Các tam giác cân: $\Delta ABC$ cân tại A, $\Delta MNP$ cân tại N.
Vận dụng 2: Cho tam giác ABC cân tại A có góc B bằng $60^{o}$. Chứng minh rằng tam giác ABC đều.
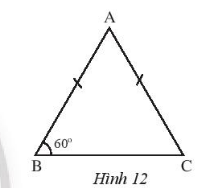
Hướng dẫn giải:
+) Vì $\Delta ABC$ có AB = AC nên $\Delta ABC$ cân tại A.
$\Rightarrow $ $\widehat{ABC}= \widehat{ACB}= 60^{o}$.
$\Rightarrow $ $\widehat{ACB} = 180^{0} - 60^{0} - 60^{0} = 60^{0}$
+) $\widehat{BAC}= \widehat{BCA}= 60^{o}$.
$\Rightarrow $ $\Delta ABC$ cân tại B
$\Rightarrow $ BA = BC.
Theo chứng minh trên: AB = AC = BC
$\Rightarrow $ $\Delta ABC$ tam giác đều.


 Chứng minh rằng:
Chứng minh rằng:
 a) Chứng minh rằng $\widehat{ABF} = \widehat{ACE}$
a) Chứng minh rằng $\widehat{ABF} = \widehat{ACE}$
Bình luận