Giải bài 6 trang 62 toán 7 tập 2 chân trời sáng tạo
Bài 6 trang 62 toán 7 tập 2 CTST
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b
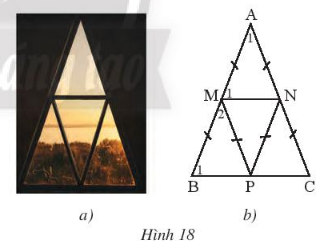
a. Cho biết $\widehat{A_{1}} = 42^{0}$. Tính số đo của $\widehat{M_{1}}$, $\widehat{B_{1}}$, $\widehat{M_{2}}$
b. Chứng minh MN // BC, MP // AC.
c. Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.
a. Vì AM = AN => Tam giác AMN cân tại A
=> $\widehat{M_{1}} = \frac{180^{o}-\widehat{A}}{2}=69^{0}$.
+ Trong tam giác ABC có AB = BC (vì AM = AN = BM = CN; AB = AM + MB; AC = AN + NC)
=> Tam giác ABC cân tại A
=> $\widehat{B_{1}} =\frac{180^{o}-\widehat{A}}{2}=69^{0}$.
+ Trong tam giác MBP có MB = MP
=> Tam giác MBP cân tại M
=> $\widehat{M_{2}} = 180^{o}- 2.\widehat{B_{1}} = 42^{0}$
b.
+ Vì $\widehat{M_{1}} = \widehat{B_{1}}$
mà 2 góc này ở vị trí đồng vị
=> MN // BC
+ Ta có: $\widehat{M_{2}} = \widehat{A_{1}} = 42^{0}$
mà hai góc ở vị trí đồng vị
=> MP // AC.
c.
+ Xét $\Delta AMN$ và $\Delta MBP$ có:
AM = MB
$\widehat{M_{2}} = \widehat{A_{1}} = 42^{0}$
AN = MP
$\Rightarrow $ $\Delta AMN$ = $\Delta MBP$ (c.g.c).
+ Xét $\Delta PMN$ và $\Delta NPC$ có:
PM = NP
$\widehat{MPN} = \widehat{PNC}$ (vì MP // AC, hai góc ở vị trí so le trong).
PN = NC
$\Rightarrow $ $\Delta PMN$ = $\Delta NPC$ (c.g.c)
+ Xét $\Delta PMN$ và $\Delta AMN$ có:
MN chung
PM = AM
PN = AN
$\Rightarrow $ $\Delta PMN$ = $\Delta AMN$ (c.c.c).
Vậy bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.
Xem toàn bộ: Giải bài 3 Tam giác cân

Bình luận