1. Phép nhân đa thức một biến

Hoạt động khám phá 1: Hãy dùng tính chất phân phối để thực hiện phép nhân x.(2x+3)

Hướng dẫn giải:

x(2x+3) = x. 2x + x .3 = $2x^{2}+3x$

Thực hành 1: Thực hiện phép nhân (4x - 3)(2x² + 5x -6)

Hướng dẫn giải:

(4x - 3)(2x² + 5x -6) = 4x.(2x² + 5x -6) - 3(2x² + 5x -6) = 8x³ + 20x²  - 24x - 6x² -15x + 18

                                  = 8x³ + 14x² - 39x +18.

Vận dụng 1: Tìm đa thức theo biến x biểu thị thể tích của hình hộp chữ nhật có kích thước như Hình 2.

Hướng dẫn giải:

Thể tích của hình hộp chữ nhật là: (x - 2)(x + 3)(x - 1).

2. Phép chia đa thức một biến

Hoạt động khám phá 2: Thực hiện phép nhân $(3x+1)(x^{2}-2x+1)$, rồi đoán xem $(3x^{3}-5x^{2}+x+1):(3x+1)$ bằng đa thức nào.

Hướng dẫn giải:

+) $(3x+1)(x^{2}-2x+1) = 3x.(x^{2}-2x+1)+1.(x^{2}-2x+1)=(3x^{3}-5x^{2}+x+1)$

+) $(3x^{3}-5x^{2}+x+1):(3x+1) = (3x+1)(x^{2}-2x+1) :(3x+1)= x^{2}-2x+1$

Thực hành 2: Thực hiện phép chia P(x) = $6x^{2}+4x$ cho Q(x) = 2x

Hướng dẫn giải: 

$(6x^{2}+4x) : 2x = (6x^{2} : 2x) + (4x:2x) = 3x +2$.

Vận dụng 2: Thực hiện các phép chia sau: $\frac{9x^{2}+5x+x}{3x}$ và $\frac{2x^{2}-3x-2}{2-x}$.

Hướng dẫn giải:

+) $\frac{9x^{2}+5x+x}{3x}$ = $\frac{9x^{2}+6x}{3x}$ = $ (9x^{2}:3x)+(6x:3x)=3x+2$.

+) $\frac{2x^{2}-3x-2}{2-x}$, ta đặt phép tính:

Vậy $\frac{2x^{2}-3x-2}{2-x}$ = -2x -1.

Thực hành 3: Thực hiện phép chia $(x^{2}+5x+9) : (x+2)$

Hướng dẫn giải: 

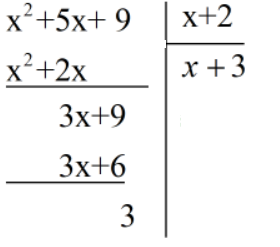
$(x^{2}+5x+9) : (x+2)$ = x + 3 dư 3.

Vận dụng 3: Tính diện tích đáy của một hình hộp chữ nhật (Hình 3) có chiều cao bằng (x + 3) cm và có thể tích bằng (x³ + 8x² + 19x+ 12) cm³.

Hướng dẫn giải:

Diện tích đáy của hình hộp chữ nhật là:  (x³ + 8x² + 19x+ 12) : (x + 3) = x² + 5x + 4.

3. Tính chất của phép nhân đa thức một biến

Thực hành 4: Thực hiện phép tính: $\frac{1}{5}(x^{2}+1).5$

Hướng dẫn giải:

$\frac{1}{5}(x^{2}+1).5 = \frac{1}{5}.5.(x^{2}+1)=x^{2}+1$.