Giải bài 3 trang 62 toán 7 tập 2 chân trời sáng tạo
Bài 3 trang 62 toán 7 tập 2 CTST
Cho tam giác ABC cân tại A có $\widehat{A} = 56^{0}$
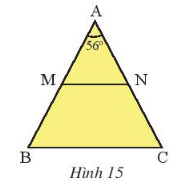
a. Tính $\widehat{B}, \widehat{C}$.
b. Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh tam giác AMN cân.
c. Chứng minh rằng MN // BC.
a. Vì tam giác ABC cân tại A $\Rightarrow $ $\widehat{B} = \widehat{C} = (180^{0} - 56^{0}) : 2 = 62^{0}$
b. Vì M, N lần lượt là trung điểm của AB, AC nên AM = MB = $\frac{AB}{2}$, AM = MC = $\frac{AC}{2}$.
mà AB = AC ( vì $\Delta ABC$ cân)
$\Rightarrow $ AM = AN
$\Rightarrow $ Tam giác AMN cân tại A.
c. Xét $\Delta AMN$ cân tại A có: $\widehat{AMN} = \frac{180^{o}-\widehat{A}}{2}$
Xét $\Delta ABC$ cân tại A có: $\widehat{ABC} = \frac{180^{o}-\widehat{A}}{2}$
$\Rightarrow $ $\widehat{AMN} = \widehat{ABC}$
mà 2 góc này ở vị trí đồng vị
$\Rightarrow $ MN // BC.
Xem toàn bộ: Giải bài 3 Tam giác cân

Bình luận