Đáp án câu 5 đề 8 kiểm tra học kì 2 toán 7

Câu 5: 

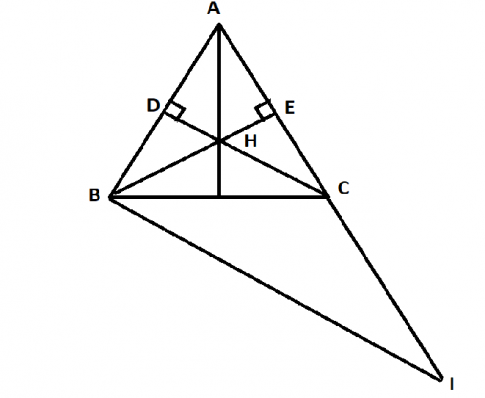
a. Tam giác ABC là tam giác đều nên đường cao BE, CD cũng đồng thời là trung tuyến hay E, D lần lượt là trung điểm của AC và AB.

Do đó AD= DB= AE= EC

Xét hai tam giác vuông BCD và CBE có

Cạnh chung BC

BD= CE (cmt)

=> $\bigtriangleup BCD=\bigtriangleup CBE$ (cạnh huyền- cạnh gọc vuông)

b. Ta có các đường cao BE, CD cũng đồng thời là đường phân giác 

=> $\widehat{ABE}=\widehat{EBC}=\widehat{ACD}=\widehat{DCB}$

Do đó $\bigtriangleup BHD=\bigtriangleup CHE$ (g.c.g)

c. $\bigtriangleup BHD=\bigtriangleup CHE$ (cmt)

=> HB= HC lại có AB= AC (gt)

Do đó AH là đường trung trực BC

d. BI // DC (gt) 

=> $\widehat{DCB}=\widehat{CBI}$ (so le trong) và $\widehat{ACD}=\widehat{I}$ (đồng vị) 

 mà $\widehat{ACD}=\widehat{DCB}$

=> $\widehat{I}=\widehat{CBI}$

Vậy $\bigtriangleup BCI$ cân