Giải câu 45 bài 5: Luyện tập ba trường hợp bằng nhau của tam giác sgk Toán hình 7 tập 1 Trang 124
Câu 45 : Trang 125 - sgk toán 7 tập 1
Đố. Cho bốn đoạn thẳng AB, BC, CD, DA trên giấy kẻ ô vuông như ở hình 110. Hãy dùng lập luận để giải thích
a) AB = CD, BC = AD
b) AB // CD
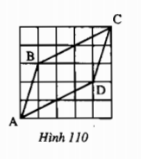

Xét ∆AHB và ∆ CKD có:
HB = KD (= 1 ô)
\(\widehat{ AHB}\) = \(\widehat{ CKD}\)
AH = CK (= 3 ô)
=> ∆AHB = ∆CKD(c.g.c)
=> AB = CD (cạnh tương ứng)
Chứng minh tương tự ta đươc: ∆ CEB = ∆ AFD (c.g.c)
suy ra BC=AD.
b) Xét ∆ABD và ∆CDB có:
AB = CD (cmt)
BC = AD (cmt)
BD chung.
=> ∆ABD = ∆CDB (c.c .c)
=> \(\widehat{ ABD}\) = \(\widehat{ CDB}\)
Mà hai góc này ở vị trí so le trong
Vậy AB // CD (đpcm)
Từ khóa tìm kiếm Google: hướng dẫn làm bài tập 45, giải bài tập 45, gợi ý giải câu 45, cách giải câu 45 Bài 5: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)

Bình luận