1. TIÊN ĐỀ EUCLID VỀ ĐƯỜNG THẲNG SONG SONG

Hoạt động 1: Cho trước đường thẳng a và một điểm M không nằm trên đường thẳng a. (H.3.31).

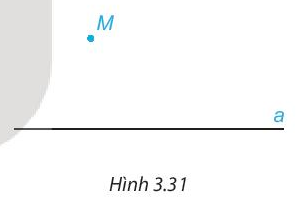
• Dùng bút chì vẽ đường thẳng b đi qua M và song song với đường thẳng a.
• Dùng bút màu vẽ đường thẳng c đi qua M và song song với đường thẳng a.

Em có nhận xét gì về vị trí của hai đường thẳng b và c?

Hướng dẫn giải:

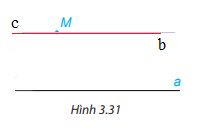
Nhận xét : Đường thẳng c và d là trùng nhau

Luyện tập 1: Phát biểu nào sau đây diễn đạt đúng nội dung của Tiên đề Euclid?

(1) Cho điểm M nằm ngoài đường thẳng a. Đường thẳng đi qua M và song song với a là duy nhất.

(2) Có duy nhất một đường thẳng song song với một đường thẳng cho trước.

(3) Qua điểm M nằm ngoài đường thẳng a, có ít nhất một đường thẳng song song với a.

Hướng dẫn giải: 

Phát biểu đúng là (1).

2. TÍNH CHẤT CỦA HAI ĐƯỜNG THẲNG SONG SONG

Hoạt động 2: Vẽ hai đường thẳng song song a,b. Kẻ đường thẳng c căt đường thẳng a tại A và cắt đường thẳng b tại B. Trên Hình 3.34:

a. Em hãy đo một cặp góc so le trong rồi rút ra nhận xét.

b. Em hãy đo một cặp góc đồng vị rồi rút ra nhận xét.

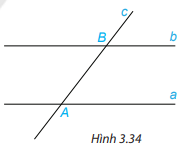
Hướng dẫn giải:

Gọi $\widehat{B_{2}}$là góc đối đỉnh với $\widehat{cBb}$

a. Đo cặp góc so le trong $\widehat{B_{2}}$ và $\widehat{cAa}$ ta sẽ có $\widehat{B_{2}}$ = $\widehat{cAa}$

b. Đo cặp góc đồng vị $\widehat{cAa}$ và $\widehat{cBb}$ ta có : $\widehat{cAa}$ = $\widehat{cBb}$

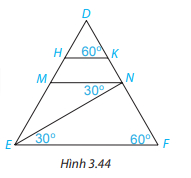
Luyện tập 2: 

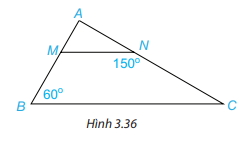
1. Cho Hình 3.36, biết MN//BC,$\widehat{ABC}=60^{\circ}$, $\widehat{MNC}=150^{\circ}$. Hãy tính số đo các góc BMN và ACB.

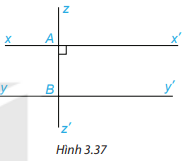
2. Cho Hình 3.37, biết rằng xx’//yy’ và zz’ ⊥

xx’. Tính số đo góc ABy và cho biết zz’ có vuông góc với yy’ không

Hướng dẫn giải:

1.

• Vì $\widehat{AMN}$ và $\widehat{ABC}$ là 2 góc đồng vị => $\widehat{AMN} = $\widehat{ABC}$ =$60^{\circ}$
• Lại có $\widehat{AMN}$ và $\widehat{BMN}$ là 2 góc kề bù => $\widehat{AMN}$ + $\widehat{BMN}$ = $180^{\circ}$=> $\widehat{BMN}$= $180^{\circ}$- $\widehat{AMN}$= $180^{\circ}$- $60^{\circ}$ = $120^{\circ}$

Tương tự :

$\widehat{ANM}$ và $\widehat{ACB}$ là 2 góc đồng vị => $\widehat{ANM} = $\widehat{ACB}$ .

Mặt khác $\widehat{ANM}$ và $\widehat{MNC}$ là 2 góc kề bù => $\widehat{ANM}$ + $\widehat{MNC}$ = $180^{\circ}$

=>$\widehat{ACB}$ + $\widehat{MNC}$ = $180^{\circ}$=> $\widehat{ACB}$= $180^{\circ}$- $\widehat{MNC}$ = $180^{\circ}$ - $150^{\circ}$ = $30^{\circ}$

2. Vì xx’//yy’ nên $\widehat{x'AB}$ = $\widehat{ABy}$ ( 2 góc so le trong)

Mà zz’⊥ xx’ nên $\widehat{x'AB}$ =  $90^{\circ}$ => $\widehat{ABy}$ = $90^{\circ}$ =>  zz’⊥ yy’