1. CÁC GÓC TẠO BỞI MỘT ĐƯỜNG THẲNG CẮT HAI ĐƯỜNG THẲNG

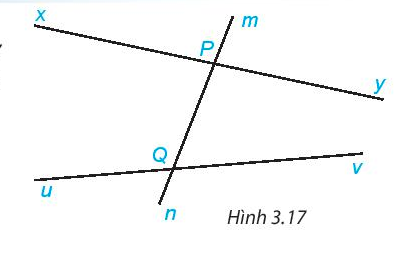
Câu hỏi 1: Cho đường thẳng mn cắt đường thẳng xy và uv lần lượt tại hai điểm P và Q (H.3.17).Em hãy kể tên:

a. Hai cặp góc so le trong

b. Bốn cặp góc đồng vị.

Hướng dẫn giải:

a. Hai  cặp góc so le trong là: $\widehat{xPn }$ và $\widehat{mQv }$;  $\widehat{yPn }$ và $\widehat{uQm}$

b. Bốn cặp góc đồng vị là: $\widehat{yPm}$ và $\widehat{mQv }$; $\widehat{yPn}$ và $\widehat{vQn }$ ; $\widehat{mPx}$ và $\widehat{mQu} $; $\widehat{xPn}$ và góc $\widehat{uQn }$

Hoạt động 1: Trên Hình 3.18, cho biết hai góc so le trong A₁ và B₃ bằng nhau và bằng $60^{\circ}$ . Hãy tính và so sánh hai góc so le trong còn lại A₂ và B₄.

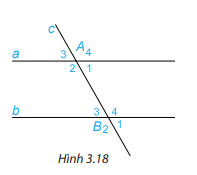
Hướng dẫn giải:

Ta có :

$\widehat{A_{2}}$ và $\widehat{A_{1}}$ là hai góc kề bù => $\widehat{A_{2}}$ = $180^{\circ}$- $\widehat{A_{1}}$ = $180^{\circ}$- $60^{\circ}$= $120^{\circ}$

$\widehat{B_{4}}$ và $\widehat{B_{3}}$ là hai góc kề bù => $\widehat{B_{4}}$ = $180^{\circ}$- $\widehat{B_{3}}$ = $180^{\circ}$- $60^{\circ}$= $120^{\circ}$

=> Vậy hai góc so le trong còn lại A₂ và B₄ bằng nhau và bằng $120^{\circ}$

Hoạt động 2: Dựa vào Hình 3.18. Chọn hai góc đồng vị rồi tính và so sánh hai góc đó.

Hướng dẫn giải:

Chọn cặp góc đồng vị: góc A₁ và góc B₄

b. Các cặp góc A₁ và B₄; A₂ và B₃ được gọi là các cặp góc trong cùng phía. Tính tổng:$\widehat{A_{1}} +\widehat{B_{1}} $ và $\widehat{A_{2}} +\widehat{B_{3}} $

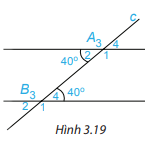
Hướng dẫn giải:

a. Vì $\widehat{A_{1}}$ và $\widehat{A_{2}}$ là 2 góc kề bù nên

$\widehat{A_{1}}$ =$180^{\circ}$ - $\widehat{A_{2}}$ = $180^{\circ}$- $40^{\circ}$= $140^{\circ}$

Lại do tính chất hai góc đối đỉnh của:

• $\widehat{A_{1}}$ và $\widehat{A_{3}}$ => $\widehat{A_{3}}$= $\widehat{A_{1}}$ = $140^{\circ}$
• $\widehat{A_{2}}$ và $\widehat{B_{4}}$ => $\widehat{B_{4}}$= $\widehat{A_{2}}$= $40^{\circ}$.

Lại có 2 góc này ở vị trí so le trong nên 2 góc đồng vị bằng nhau

=> $\widehat{A_{1}}$ = $\widehat{B_{1}}$=$140^{\circ}$

$\widehat{A_{2}}$ = $\widehat{B_{2}}$=$40^{\circ}$.

$\widehat{A_{3}}$ = $\widehat{B_{3}}$=$140^{\circ}$

$\widehat{A_{4}}$ = $\widehat{B_{4}}$=$40^{\circ}$

2. DẤU HIỆU NHẬN BIẾT HAI ĐƯỜNG THẲNG SONG SONG

Luyện tập 2: 

1. Quan sát Hình 3.22 và giải thích vì sao AB // CD.

2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song?

Hướng dẫn giải:

a. Ta có : $\widehat{BAx}$ và $\widehat{CDA}$ bằng nhau và bằng $60^{\circ}$.

Mặt khác 2 góc này ở vị trí so le trong

=> AB // CD.

b. Ta có : $\widehat{zKy'}$ và $\widehat{z'Ky'}$ là hai góc kề bù nên $\widehat{z'Ky'}$= $180^{\circ}$- $\widehat{zKy'}$ = $180^{\circ}$ - $90^{\circ}$ = $90^{\circ}$

=> $\widehat{z'Ky'}$ = $\widehat{z'Hy}$ . Mặt khác 2 góc này lại ở vị trí đồng vị nên xy // x'y'

Thực hành 1: Cho đường thẳng a và điểm A nằm ngoài đường thẳng a. Để vẽ đường thẳng b đi qua A và song song với a, ta có thể sử dụng góc nhọn $60^{\circ}$

của êke để vẽ như sau:

Tại sao khi vẽ như trên ta lại khẳng định được hai đường thẳng a và b song sọng với nhau.

Hướng dẫn giải:

Theo cách vẽ trên thì góc A và B có số đo bằng nhau (đều bằng $60^{\circ}$). Mà 2 góc này ở vị  trí đồng vị => a//b

Thực hành 2: Dùng góc vuông hay góc $30^{\circ}$ của êke (thay cho góc $60^{\circ}$) để vẽ đường thẳng đi qua và song song với đường thẳng a cho trước.

Hướng dẫn giải:

• Dùng góc vuông:

B1: Vẽ đường thẳng a , điểm A nằm ngoài đường thẳng a

B2: Đặt ê ke sao cho 1 cạnh của góc vuông của ê ke nằm trên đường thẳng a, 1 cạnh góc vuông còn lại đi qua điểm A, rồi kẻ đường thẳng b vuông góc với a và đi qua A.

B3: Kẻ đường thẳng vuông góc với đường thẳng b và đi qua A .

Như vậy Ta được đường thẳng b đi qua A và song song với a.

• Dùng góc $60^{\circ}$ của êke:

B1: Vẽ đường thẳng a , điểm A nằm ngoài đường thẳng a

B2: Đặt ê ke sao cho góc nhọn $30^{\circ}$ và 1 cạnh của góc vuông của ê ke nằm trên đường thẳng a, cạnh đối diện với góc vuông đi qua điểm A, ta kẻ đường thẳng c đi qua cạnh đối diện với góc vuông của ê ke.

B3: Dịch chuyển ê ke theo đường thẳng c cho đến khi điểm A trùng với đỉnh của góc nhọn  $30^{\circ}$

B4: Kẻ đường thẳng b đi qua A và 1 cạnh của góc $30^{\circ}$

Như vậy Ta được đường thẳng b đi qua A và song song với a.