KHỞI ĐỘNG

Câu hỏi: Trên mặt đồng hồ ở Hình 1, quan sát hai góc: góc tạo bởi kim giờ và kim phút; góc tạo bởi kim phút và kim giây.

Hai góc đó có liên hệ gì đặc biệt?

Hướng dẫn giải:

Quan sát mặt đồng hồ hình 1 ta thấy: Hai góc được đánh dấu có:

• Chung đỉnh
• Chung một cạnh
• Kim giờ và kim giây nằm về hai phía của kim phút.

I. HAI GÓC KỀ NHAU

Luyện tập 1: Ở Hình 6, hai góc xOy và mOn có phải là hai góc kề nhau hay không? Vì sao?

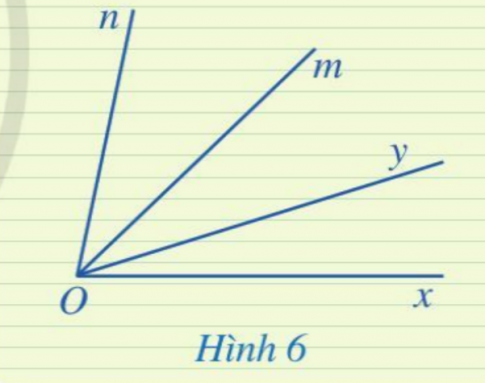
Hướng dẫn giải:

Hai góc xOy và mOn không phải là hai góc kề nhau vì không có cạnh nào chung.

Luyện tập 2: Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp.

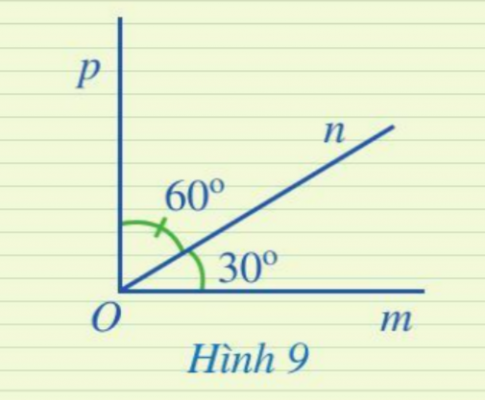
Hướng dẫn giải:

Hai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.

Vì On nằm trong góc mOp nên

$\widehat{mOn}+\widehat{nOp}=>30^{0}+60^{0}=\widehat{mOp}$

$=>\widehat{mOp}=90^{0}$

II. HAI GÓC BÙ NHAU. HAI GÓC KỀ BÙ

Hoạt động 3: Tìm tổng số đo của góc $110^{0}$ và góc $70^{0}$

Hướng dẫn giải:

Tổng số đo của hai góc là: $110^{0} + 70^{0} = 180^{0}$

Hoạt động 4: Quan sát hai góc xOt và yOt ở Hình 10, trong đó Ox và Oy là hai tia đối nhau.

a) Hai góc xOt và yOt có kề nhau không?

b) Tính $\widehat{xOt}+\widehat{yOt}$

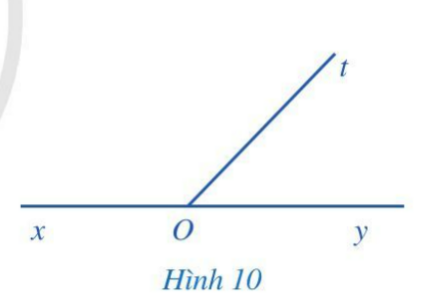
Hướng dẫn giải:

a) Hai góc xOt và yOt là hai góc kề nhau vì có đỉnh O chung, cạnh Ot chung, 2 cạnh còn lại là Ox và Oy nằm về hai phía so với đường thẳng chứa tia Ot

b) Vì tia Ot nằm trong góc xOy nên: $\widehat{xOt}+\widehat{yOt} = \widehat{xOy}$

Mà $\widehat{xOy}= 180^{0}$ (góc bẹt)

=> $\widehat{xOt}+\widehat{yOt} =180^{0}$

Luyện tập 3: Tính góc xOt trong hình 12

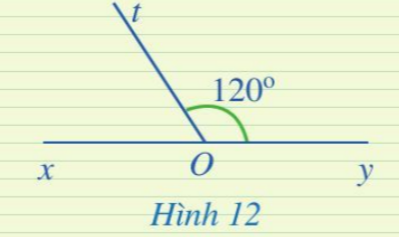
Hướng dẫn giải:

Ta có: $\widehat{xOt}+\widehat{tOy} =180^{0}$ (hai góc kê bù)

=> $\widehat{xOt}+120^{0} = 180^{0}$

=> $\widehat{xOt} = 180^{0} - 120^{0}= 60^{0}$

III. HAI GÓC CỐ ĐỊNH

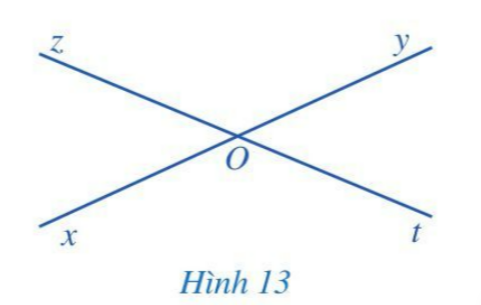
Hoạt động 5: Quan sát hai góc xOz và yOt ở Hình 13, trong đó, Ox và Oy là hai tia đối nhau, Oz và Ot cũng là hai tia đối nhau và cho biết:

a) Cạnh Ox của góc xOz là tia đối của cạnh nào của góc yOt.

b) Cạnh Oz của góc xOz là tia đối của cạnh nào của góc yOt.

Hướng dẫn giải:

a) Cạnh Ox của góc xOz là tia đối của cạnh Oy của góc yOt.

b) Cạnh Oz của góc xOz là tia đối của cạnh Ot của góc yOt.

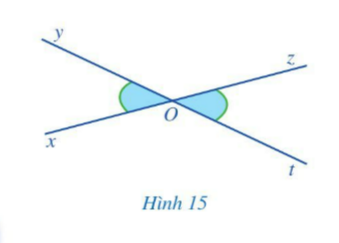
Hoạt động 6: Quan sát Hình 15 và giải thích vì sao:

a) Hai góc xOy và yOz là hai góc kề bù;

b) Hai góc yOz và zOt là hai góc kề bù;

c) $\widehat{xOy}+\widehat{yOz}=\widehat{yOz}+\widehat{zOt}$ và $\widehat{xOy}=\widehat{zOt}$

Hướng dẫn giải:

a) Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz nằm về hai phía đối với đường thẳng chứa tia Oy nên hai góc xOy và yOz là hai góc kề nhau. Hơn nữa, hai góc xOy và yOz có tổng bằng góc xOz =180 độ nên hai góc xOy và yOz là hai góc bù nhau.

Vậy hai góc xOy và yOz là hai góc kề bù

b) Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot nằm về hai phía đối với đường thẳng chứa tia Oz nên hai góc yOz và zOt là hai góc kề nhau. Hơn nữa, hai góc yOz và zOt có tổng bằng góc xOz =180 độ nên hai góc yOz và zOt là hai góc bù nhau.

Vậy hai góc yOz và zOt là hai góc kề bù

c. Do $\widehat{xOy}+\widehat{yOz}=\widehat{xOz}=180^{0}$

        $\widehat{yOz}+\widehat{zOt}=\widehat{yOt}=180^{0}$

Vậy $\widehat{xOy}+\widehat{yOz}=\widehat{yOz}+\widehat{zOt}$

$=>\widehat{xOy}=\widehat{zOt}$

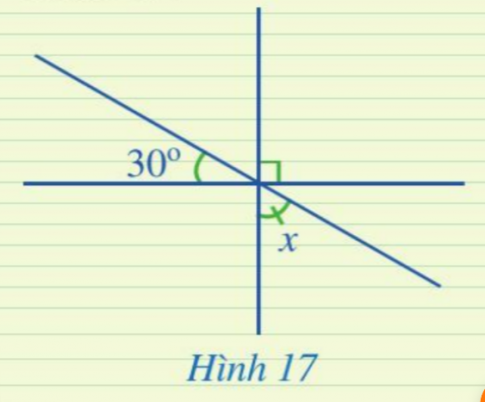
Luyện tập 4: Tìm số đo x trong Hình 17

Hướng dẫn giải:

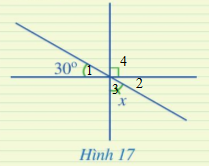
Ta có: $\widehat{O_{1}}=\widehat{O_{2}}$ (hai góc đối đỉnh). Mà $\widehat{O_{1}}=30^{0}=>\widehat{O_{2}}=30^{0}$

Ta có: $\widehat{O_{2}}+\widehat{O_{3}}+\widehat{O_{4}}=180^{0}$ (góc kế bù)

$=>x+30^{0}+90^{0}=180^{0}$

$=>x=180-30^{0}-90^{0}=60^{0}$