Giải bài 5: Trường hợp bằng nhau thứ ba của tam giác góc cạnh góc (g.c.g) sgk Toán hình 7 tập 1 Trang 121 125
Nếu hai tam giác có 1 cạnh và 2 góc kề bằng nhau thì hai tam giác đó có bằng nhau không ? Để biết thêm chi tiết, Tech12h xin chia sẻ với các bạn bài: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g). Với lý thuyết và các bài tập có lời giải chi tiết, hi vọng rằng đây sẽ là tài liệu giúp các bạn học tập tốt hơn.

Nội dung bài viết gồm 2 phần:
- Ôn tập lý thuyết
- Hướng dẫn giải bài tập sgk
A. LÝ THUYẾT
Trường hợp bằng nhau góc - cạnh - góc của hai tam giác.
Tính chất:
- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kìa thì hai tam giác đó bằng nhau.
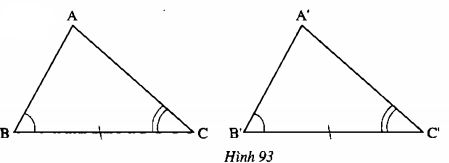
Nếu ∆ABC và ∆ A'B'C ' có:
\(\left.\begin{matrix} \widehat{B}=\widehat{B'}\\ BC=B'C' \\ \widehat{C}=\widehat{C'} \end{matrix}\right\}\)
thì ∆ABC = ∆ A'B'C'
Hệ quả:
- Hệ quả 1: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
- Hệ quả 2. Nếu cạnh huyền và góc nhọn của tam giác vuông nay bằng cạnh huyền, góc nhỏn của tam giác vuông kiathì hai tam giác vuông đó bằng nhau.





Bình luận