Giải câu 35 bài 5: Trường hợp bằng nhau thứ ba của tam giác góc cạnh góc (g.c.g) sgk Toán hình 7 tập 1 Trang 123
Câu 35 : Trang 123 - sgk toán 7 tập 1
Cho góc xOy khác góc bẹt, Ot là tia phân giác của góc đó. Qua H thuộc tia Ot , kẻ đường vuông góc với Ot, nó cắt Ox và Oy theo thứ tự A và B.
a) Chứng minh rằng OA = OB.
b ) Lấy điểm C thuộc tia Ot, chứng minh rằng CA = CB và \(\widehat{OAC }\) = \(\widehat{OBC }\).
Theo giả thiết ta có hình vẽ sau:
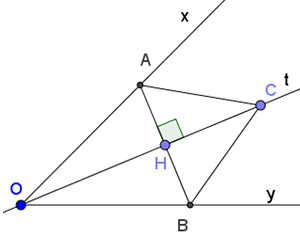
a) Xét tam giác vuông ∆AOH và tam giác vuông ∆BOH có:
\(\widehat{AOH}\) = \(\widehat{BOH}\) (Do Ot là tia phân giác của góc xOy )
OH là cạnh chung
=> ∆AOH =∆BOH( cạnh huyền góc nhọn)
=> OA = OB (cạnh tương ứng).
b) Xét ∆AOC và ∆BOC có:
OA = OB (chứng minh trên)
\(\widehat{OAC}\) = \(\widehat{OAB}\) (Do Ot là tia phân giác của góc xOy)
OC : cạnh chung.
=> ∆AOC = ∆BOC (g.c.g)
=> CA = CB (cạnh tương ứng)
=> \(\widehat{OAC }\) = \(\widehat{OBC }\) ( góc tương ứng) (đpcm)

Bình luận