CHƯƠNG V - ĐƯỜNG TRÒN

BÀI 3 - TIẾP TUYẾN ĐƯỜNG TRÒN

19. Cho đường tròn tâm O bán kính 15 cm. Điểm A nằm ngoài đường tròn sao cho OA = 25cm Kẻ tiếp tuyến AB của đường tròn (O). Kẻ dây BC vuông góc với OA tại H.

a) Chứng minh AC là tiếp tuyến của đường tròn (O).

b) Tính độ dài các cạnh của tam giác ABC.

Bài giải chi tiết:

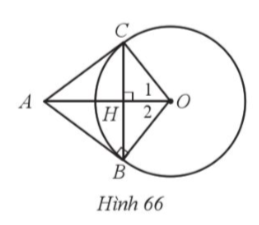
a) Vì (cạnh huyền - cạnh góc vuông) nên .

Từ đó, ta chứng minh được (c.g.c). Suy ra hay vuông góc với tại . Vậy là tiếp tuyến của đường tròn . 

b) Do tam giác vuông tại nên

Vì nên hay .

Do nên hay .

Do nên .

Vậy tam giác có và .

20. Cho đường tròn (O) và dây AB khác đường kính. Kẻ bán kính OC đi qua trung điểm 1 của đoạn thẳng AB. Vẽ đường tròn (C; CI). Kẻ tiếp tuyến BD của đường tròn (C) với D là tiếp điểm và D khác 1. Chứng minh:

a) Bốn đĩnh của tứ giác BDCI cùng nằm trên một đường tròn;

b) BD là tiếp tuyến của đường tròn (O).

Bài giải chi tiết:

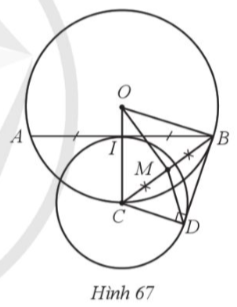
a) Gọi là trung điểm của đoạn thẳng (Hình 67). Ta chứng minh được là đường trung trực của đoạn thẳng .

Do tam giác vuông tại và tam giác vuông tại nên

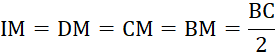
Do đó bốn đỉh của tứ giác cùng nằm trên đường tròn đường kính .

b) Do là tiếp tuyến của đường tròn nên .

Mà (vi tam giác cân tại ) hay , suy ra .

Ta lại có nên hay .

Suy ra vuông góc với tại . Vậy là tiếp tuyến của đường tròn .

21. Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho = 30°. Lấy điểm M sao cho B là trung điểm của đoạn thẳng OM. Chứng minh:

a) MC là tiếp tuyến của đường tròn (O);

b) MC = R√3.

Bài giải chi tiết:

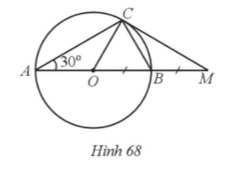
a) Ta chứng minh được tam giác vuông tại và .

Suy ra . 

Mà tam giác cân tại , suy ra tam giác đều hay . Do đó tam giác vuông tại hay vuông góc với tại .

Vâyy là tiếp tuyến của đường tròn .

b) Do tam giác vuông tại nên

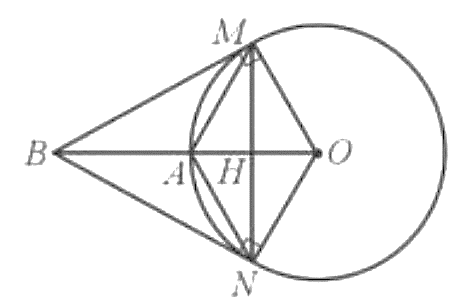
22. Cho đường tròn (O; R) và điểm A năm trên đường tròn. Lấy điểm B sao cho A là trung điểm của đoạn thẳng OB. Kẻ hai tiếp tuyến BM, BN của đường tròn (O).

a) Tính số đo góc và độ dài đoạn thẳng BM theo R.

b) Tứ giác AMON là hình gì ? Vì sao?

c) Tính độ dài đoạn thẳng OH theo R với H là giao điểm của OA và MN.

Bài giải chi tiết:

a) Do là tiếp tuyến của đường tròn nên và .

Vi tam giác vuông tại nên

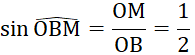
Suy ra . Do đó

Hình 69

Do tam giác vuông tại nên

b) Ta chứng minh được các tam giác đều.

Suy ra . Do đó tứ giác là hình thoi.

c) Do tứ giác là hình thoi nên .

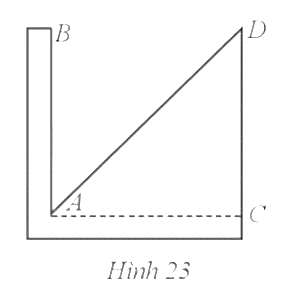
23. Hình 23 minh hoạ thước phân giác. Thước gồm hai thanh gỗ ghép lại thành góc vuông và một tấm gỗ có dạng hình tam giác ACD với AD là tia phân giác của góc . Có thể dùng thước phân giác để tìm tâm của một hình tròn hay không? Vì sao? 

Bài giải chi tiết:

Để tìm tâm của một hình tròn, ta đặt hình tròn đó tiếp xúc với hai cạnh và . Vạch theo ta được một đường thẳng đi qua tâm của hình tròn. Xoay hình tròn và làm tương tự, ta được một đường thẳng nữa đi qua tâm của hình tròn. Giao điểm của hai đường vừa kẻ là tâm của hình tròn (Hinh 70 ).

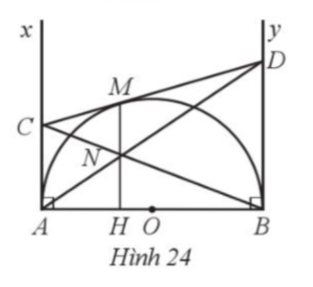
24. Cho nửa đường tròn tâm O đường kính AB. Kẻ các tiếp tuyến Ax, By của đường tròn (O). Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyển thứ ba cắt Ax, By lần lượt tại C, D. Gọi M là giao điểm của AD và BC và H là giao điểm của MN và AB (Hình 24). Chứng minh: 

a) MN

b) MN = NH.

Bài giải chi tiết:

a) Ta chứng minh được .

Do là tiếp tuyến của đường tròn nên .

Mà (vi tam giác có , suy ra .

Do đó . Suy ra hay .

b) Do nên theo định li Thalès, ta có:

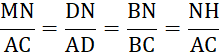
Do đó .

25. Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài với nhau tại A với Rr.

Đường nối  lần lượt cắt hai đường tròn (O) và (O) tại B và C. Đường thẳng a lần lượt tiếp xúc với hai đường tròn (O) và (O) tại D và E. Gọi M là giao điểm của BD và CE. Chứng minh:

a) DME = 90°;

b) MA tiếp xúc với hai đường tròn (O) và (O’);

c) MD.MBME.MC.

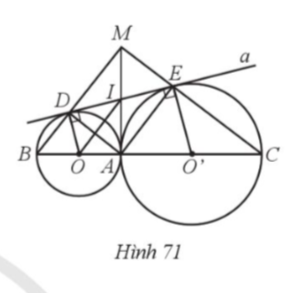
Bài giải chi tiết:

Gọi là giao điểm của và .

a) Ta chứng minh được . Suy ra

Mà tam giác cân tại và tam giác cân tai , suy ra .

Vì hai tam giác cân tại nên 

Mà và , suy ra

Do đó .

Ta lại có nên hay .

b) Ta chứng minh được tứ giác là hình chữ nhật. Suy ra .

Do đó (c.c.c). Suy ra hay vuông góc với tại .

Vậy tiếp xúc với hai đường tròn và .

c) Do nên . Suy ra .

26. Cho tam giác ABC vuông tại A có đường cao AH. Hình chiều của H trên AB, AC lần lượt là D, E. Gọi (O) là đường tròn đường kính HB và (O’) là đường tròn đường kính HC. Chứng minh:

a) Điểm D thuộc đường tròn (O) và điểm E thuộc đường tròn (O’);

b) Hai đường tròn (O) và (O’) tiếp xúc ngoài;

c) AH là tiếp tuyến chung của hai đường tròn (O) và (O’)

d) AH DE

e) Diện tích tứ giác DEO’O bằng nửa diện tích tam giác ABC.

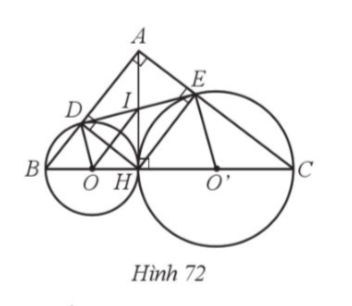
Bài giải chi tiết:

Gọi là giao điểm của và (Hinh 72 ). 

a) Do tam giác vuông tại nên

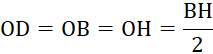
Vậy điểm thuộc đường tròn .

Tương tự, ta chứng minh được điểm thuộc đường tròn .

b) Do nên hai đường tròn và tiếp xúc ngoài tại .
c) Do vuông góc với 'tại nên là tiếp tuyến chung của hai đường tròn và .

d) Ta chứng minh được tứ giác là hình chữ nhật. Suy ra .

e) Do (c.c.c) nên hay .

Tương tự, ta chứng minh được .

Do đó tứ giác là hình thang có là đường cao.

Diện tích hình thang và tam giác lần lượt là:

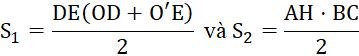
Mà và , suy ra .

Vậy diện tích tứ giác bằng nửa diện tích tam giác .