BÀI 3. TIẾP TUYẾN CỦA ĐƯỜNG TRÒN

Mở đầu: Quan sát máy cắt máy cắt sắt đang hoạt động (Hình 32), ta thấy các mảnh vụn sắt chuyển động và văng ra theo phương tiếp tuyến với đường tròn mép đĩa sắt. Tiếp tuyến của đường tròn có tính chất gì và được nhận biết như thế nào?

Giải rút gọn:

Tiếp tuyến của đường tròn vuông góc với bán kính đi qua tiếp điểm.

I. NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN

Hoạt động 1 (trang 106) 

Cho đường thẳng a là tiếp tuyến của đường tròn (O; R). Gọi H là hình chiếu của tâm O trên đường thẳng a (Hình 33).

a) So sánh khoảng cách OH từ tâm O đến đường thẳng a và bán kính R.

b) Điểm H có thuộc đường tròn (O; R) hay không?

c) Điểm H có phải là tiếp điểm của đường thẳng a và đường tròn (O; R) hay không?

d) Đường thẳng a có vuông góc với bán kính đi qua tiếp điểm hay không?

Giải rút gọn:

a) OH = R

b) Điểm H thuộc đường tròn (O; R)

c) Điểm H là tiếp điểm của đường thẳng a và đường tròn (O; R)

d) Đường thẳng a vuông góc với bán kính và đi qua tiếp điểm.

Luyện tập, vận dụng 1 (trang 107) 

Cho ba điểm A, B, C thẳng hàng, trong đó B nằm giữa A và C. Đường tròn (O) tiếp xúc với đường thẳng AB tại điểm C. 

Chứng minh:

Giải rút gọn:

⇒

Hoạt động 2 (trang 107)

Cho đường thẳng a và đường tròn (O; R) thỏa mãn đường thẳng a đi qua điểm H thuộc đường tròn (O;R) và a vuông góc với OH. Lấy điểm N thuộc đường thẳng a và N khác H (Hình 35).

a) So sánh khoảng cách từ điểm O đến đường thẳng a và bán kính R.

b) So sánh ON và R. Điểm N có thuộc đường tròn (O; R) hay không?

c) Đường thẳng a có phải là tiếp tuyến của đường tròn (O; R) hay không?

Giải rút gọn:

a) OH = R 

b) Xét vuông tại H:

ON là cạnh huyền

⇒ ON > R.

c) Đường thẳng a là tiếp tuyến của đường tròn (O; R)

Luyện tập, vận dụng 2 (trang 107)

Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài nhau tại điểm I. Gọi d là tiếp tuyến của (O; R) tại điểm I. Chứng minh d là tiếp tuyến của (O’; R’).

Giải rút gọn:

d là tiếp tuyến của (O; R) tại I ⇒

Mà I tại I

⇒ là tiếp tuyến của đường tròn (O’; R’).

Luyện tập, vận dụng 3 (trang 108)

Cho hai đường tròn (O), (O’) cắt nhau tại điểm A, B sao cho đường thẳng OA là tiếp tuyến của đường tròn (O’). Chứng minh đường thẳng O’B là tiếp tuyến của đường tròn (O).

Giải rút gọn:

OA là tiếp tuyến của đường tròn (O’)

Xét có:

OA = OB

O’A = O’B 

OO’ chung

tại B

Vậy O’B là tiếp tuyến của đường tròn (O).

II. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU

Hoạt động 3 (trang 108)

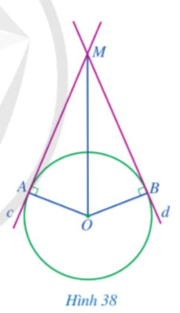
Cho đường tròn (O; R). Các đường thẳng c, d lần lượt tiếp xúc với đường tròn (O; R) tại A, B và cắt nhau tại M (Hình 38).

a) Các tam giác MOA và MOB có bằng nhau hay không?

b) Hai đoạn thẳng MA và MB có bằng nhau hay không?

c) Tia MO có phải là tia phân giác của góc AMB hay không?

d) Tia OM có phải là tia phân giác của góc AOB hay không?

Giải rút gọn:

a)

b)

c)

d)

Luyện tập, vận dụng 4 (trang 109)

Cho đường tròn (O; R) và điểm M nằm ngoài đường tròn. Hai đường thẳng c, d qua M lần lượt tiếp xúc với (O) tại A, B. Biết = 120. Chứng minh AB = R.

Giải rút gọn:

Xét  

OA = OB = AB = R (đpcm).

III. GIẢI BÀI TẬP CUỐI SGK

Bài 1 (trang 109)

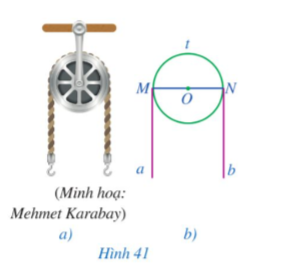
Ròng rọc là một loại máy cơ đơn giản có rãnh và có thể quay quanh một trục, được sử dụng rộng rãi trong công việc nâng lên và hạ xuống vật nặng trong cuộc sống. Trong Hình 41a, có một sợi dây không dãn vắt qua ròng rọc.

Gả sử ròng rọc được minh họa bởi đường tròn (O) sợi dây vắt qua ròng rọc được minh họa bởi nửa đường tròn MtN và hai tiếp tuyến Ma, Nb của đường tròn (O) (Hình 41b). Chứng minh Ma // Nb.

Giải rút gọn:

Ma là tiếp tuyến

Nb là tiếp tuyến

3 điểm M, O, N thẳng hàng

Ma

Bài 2 (trang 110)

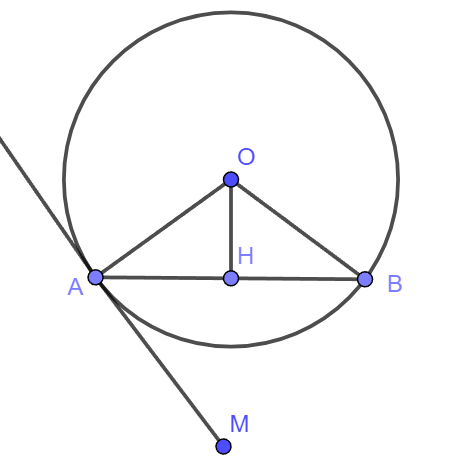
Cho đường tròn (O) và dây AB. Điểm M nằm ngoài đường tròn (O) thỏa mãn điểm B nằm trong góc MAO và Chứng minh đường thẳng MA là tiếp tuyến của đường tròn (O).

Giải rút gọn:

Kẻ OH AB tại H

Xét OA = OB = R

⇒ cân tại O

⇒ OH đồng thời là đường phân giác

=

⇒

⇒

hay = 90

⇒ MA OA

⇒ MA là tiếp tuyến của đường tròn (O)

Bài 3 (trang 110)

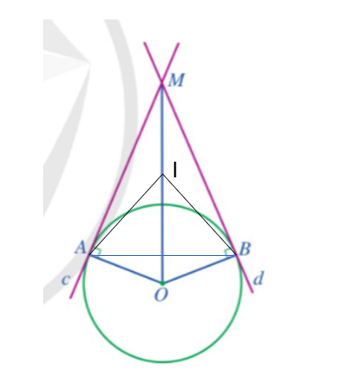
Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Hai đường thẳng c, d đi qua M lần lượt tiếp xúc với (O) tại A, B. Tia phân giác của góc MAB cắt MO tại I. Chứng minh điểm I cách đều ba đường thẳng MA, MB và AB.

Giải rút gọn:

Xét  

MO là đường phân giác của (MA và MB là 2 đường tiếp tuyến của đường tròn (O))

AI là đường phân giác của  

⇒ I là cách đều MA, AB, MB.

Bài 4 (trang 110)

Một người quan sát đặt mắt ở vị trí A có độ cao cách mực nước biển là AB = 5m. Cắt bề mặt trái đất bởi một mặt phẳng đi qua điểm A và tâm của Trái Đất thì phần chung giữa chúng là một đường tròn lớn tâm O. Tầm quan sát tối đa từ vị trí A là đoạn thẳng AC, trong đó C là tiếp điểm của tiếp tuyến đi qua A với đường tròn (O) (minh họa như Hình 42). Tính độ dài đoạn thẳng AC (theo đơn vị kilômét và làm tròn kết quả đến hàng phần mười), biết bán kính Trái Đất là OB = OC

(Nguồn: Toán 9 – Tập một, NXB giáo dục Việt Nam, năm 2017).

Giải rút gọn:

Với OB = OC

→ AC 253 km.

Bài 5 (trang 110)

Cho đường tròn (O; R) đường kính AB và các đường thẳng m, n, p lần lượt tiếp xúc với đường tròn tại A, B, C (Hình 43). Chứng minh:

a) AD + BE = DE;

b)

c) Tam giác ODE vuông;

d) .

Giải rút gọn:

Đường thẳng m, n, p tiếp xúc đường tròn tại A, B, C nên:

AD = CD; CE = BE

DO là đường phân giác của

EO là đường phân giác của

a) (đpcm) 

b) DO là đường phân giác của ⇒ (đpcm)

EO là đường phân giác của ⇒

c) = + = + = = 90

⇒ ODE vuông tại O 

 d) S_ODE = OD.OE = OC.DE

⇒ OD.OE = OC.DE = R.DE

⇒ (đpcm)