BÀI 1. ĐƯỜNG TRÒN. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN

Mở đầu: Mỗi bánh xe đạp ở Hình 1 gợi nên hình ảnh của một đường tròn.

Hai đường tròn đó có điểm chung hay không?

Giải rút gọn:

Điểm chung: bán kính bằng nhau.

I. KHÁI NIỆM ĐƯỜNG TRÒN

Hoạt động 1 (trang 93):

Đồng hồ được mô tả ở Hình 2 có kim phút dài 12 cm. Khi kim phút quay một vòng thì đầu mút của kim phút vạch nên đường gì?

Giải rút gọn:

Đầu mút của kim phút vạch nên đường tròn.

Luyện tập, vận dụng 1 (trang 94):

Hãy chỉ ra một số đồ vật trong thực tiễn gợi nên hình ảnh của đường tròn.

Giải rút gọn:

Cái mâm, cái bát, bánh xe đạp, đồng hồ,...

II. LIÊN HỆ GIỮA ĐƯỜNG KÍNH VÀ DÂY CỦA ĐƯỜNG TRÒN

Hoạt động 2 (trang 94):

Quan sát Hình 5,

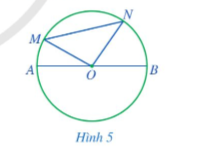
a) So sánh MN và OM + ON.

b) So sánh MN và AB.

Giải rút gọn:

a) MN < OM + ON

b) MN < AB vì AB = OM + ON. 

Luyện tập, vận dụng 3 (trang 95):

Cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh MN < BC.

Giải rút gọn:

Xét đường tròn (O):

MN là dây cung

BC là đường kính

⇒ MN < BC

III. TÍNH ĐỐI XỨNG CỦA ĐƯỜNG TRÒN

Hoạt động 3 (trang 95):

Cho đường tròn (O; R).

a) Vẽ đường thẳng d đi qua tâm O cắt đường tròn tại A, B. So sánh OA và OB (Hình 7).

b) Giả sử M là một điểm tùy ý trên đường tròn (O; R). Trên tia đối của tia OM, ta lấy điểm N sao cho ON = OM. Điểm N có thuộc đường tròn (O; R) hay không?

Giải rút gọn:

a) OA = OB

b) Điểm N thuộc đường tròn (O; R).

Hoạt động 4 (trang 95):

Cho đường tròn (O; R). Giả sử d là đường thẳng đi qua tâm O, M là một điểm tùy ý trên đường tròn (O; R) và M không thuộc d. Kẻ MH vuông góc với d tại H. Trên tia MH lấy điểm N sao cho H là trung điểm của MN (ta gọi điểm N là điểm đối xứng với điểm M qua đường thẳng d). Điểm N có thuộc đường tròn (O; R) hay không?

Giải rút gọn:

Xét ∆ OMH và ∆ ONH:
= =

MH = NH (H là trung điểm của MN);
OH là cạnh chung.
⇒ ∆OMH = ∆ONH
→ OM = ON 

M thuộc đường tròn (O; R) ⇒ OM = R ⇒ ON = R, do đó N ∈ (O; R).

Luyện tập, vận dụng 3 (trang 96):

Bạn Hoa có một tờ giấy hình tròn. Nêu cách gấp giấy để xác định tâm của hình tròn đó.

Giải rút gọn:

Để xác định tâm của tờ giấy hình tròn mà không cần dụng cụ đo lường, bạn có thể thực hiện theo cách sau:

Bước 1. Gấp đôi tờ giấy sao cho hai mép của tờ giấy trùng khít lên nhau ta
được hình nửa đường tròn.
Bước 2. Tiếp tục gấp đôi tờ giấy hình nửa đường tròn đó sao cho mép của tờ giấy trùng khít lên nhau.
Bước 3. Mở tờ giấy ra ta thấy xuất hiện giao của hai đường kính, đó chính là tâm hình tròn cần tìm.

IV. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN

Hoạt động 5 (trang 96): 

Bạn Đan vẽ năm vòng tròn minh họa cho biểu tượng của Thế vận hội Olympic như ở Hình 10. Hình vẽ đó thể hiện những cặp đường tròn cắt nhau. Theo em, hai đường tròn cắt nhau thì chúng có bao nhiêu điểm chung?

Giải rút gọn:

Hai đường tròn cắt nhau có hai điểm chung.

Luyện tập, vận dụng 4 (trang 97)

Cho hai đường tròn (O; 14 cm), (O’; 5 cm) với OO’ = 8 cm. Hỏi hai đường tròn đó có cắt nhau hay không?

Giải rút gọn:

Bán kính của (O), (O’) lần lượt là R = 14 cm, r = 5 cm.

OO’ = 8 (cm)

R – r = 9 (cm)

⇒ OO’ < R - r (8 < 9)

⇒ Hai đường tròn không cắt nhau.

Hoạt động 6 (trang 97) 

Hình 12 mô tả các ống tròn xếp lên nhau và gợi nên hình ảnh các cặp đường tròn tiếp xúc nhau. Theo em, hai đường tròn tiếp xúc nhau thì chúng có bao nhiêu điểm chung?

Giải rút gọn:

Hai đường tròn tiếp xúc nhau có 1 điểm chung.       

Luyện tập, vận dụng 5 (trang 98):

Cho hai đường tròn (O; 2,5 cm) và (O’; 4,5 cm). Tìm độ dài đoạn thẳng OO’, biết hai đường tròn đó tiếp xúc nhau.

Giải rút gọn:

Tiếp xúc ngoài: OO’ = R + r = 4,5 + 2,5 = 7 cm.

Tiếp xúc trong: OO’ = R – r = 4,5 – 2,5 = 2 cm.

Hoạt động 7 (trang 98) 

Hình 14 mô tả hai bánh xe rời nhau, gợi nên hình ảnh hai đường tròn không giao nhau. Theo em, hai đường tròn không giao nhau thì có bao nhiêu điểm chung?

Giải rút gọn:

Hai đường tròn không giao nhau thì không có điểm chung.

Luyện tập, vận dụng 6 (trang 99) 

Cho hai đường tròn (O; 11,5 cm) và (O’; 6,5 cm). Biết rằng OO’ = 4 cm. Xét vị trí tương đối của hai đường tròn đó.

Giải rút gọn:

Bán kính của (O), (O’) lần lượt là R = 11,5 cm, r = 6,5 cm.

OO’ = 4 cm

R – r = 5 cm.

⇒ OO’ < R – r (4 < 5)

Vậy đường tròn (O; 11,5 cm) đựng đường tròn (O’; 6,5 cm).

V. GIẢI BÀI TẬP CUỐI SGK 

Bài 1 (trang 99) 

Trong Hình 16, có ba đường tròn với các đường kính lần lượt là AB, AC, CD. Hãy sắp xếp độ dài ba đoạn thẳng AB, AC, CD theo thứ tự tăng dần và giải thích kết quả tìm được.

Giải rút gọn:

CD < AC < AB.

Giải thích: 3 điểm đều chung 1 gốc C nhưng bán kính lại khác nhau

Bài 2 (trang 100)

Xác định vị trí tương đối của hai đường tròn (O) và (O’) trong mỗi hình 17a, 17b, 17c, 17d:

Giải rút gọn:

Hình 17a: Hai đường tròn không cắt nhau

Hình 17b: Hai đường tròn tiếp xúc nhau

Hình 17c: Hai đường tròn không giao nhau

Hình 17d: Hai đường tròn cắt nhau.

Bài 3 (trang 100)

Cho đoạn thẳng MN và đường thẳng a là đường trung trực của đoạn thẳng MN. Điểm O thuộc đường thẳng a. 

a) Vẽ đường tròn tâm O bán kính R = OM.

b) Chứng minh điểm N thuộc đường tròn (O; R).

Giải rút gọn:

a)

b) a là đường trung trực của MN 

⇒ OM = ON = R

⇒ N thuộc đường tròn (O; R).

Bài 4 (trang 100)

Cho đường tròn (O; R) và dây AB = R. Tính số đo góc AOB.

Giải rút gọn:

Xét OA = OB = AB = R 

Bài 5 (trang 100)

Chiếc đồng hồ trang trí ở Hình 18 gợi nên vị trí tương đối của các đường tròn. Quan sát Hình 18 và chỉ ra một cặp đường tròn:

a) Cắt nhau;

b) Tiếp xúc ngoài;

c) Tiếp xúc trong;

d) Không giao nhau.

Giải rút gọn:

a) Đường tròn màu tím cắt đường tròn màu vàng

b) Đường tròn màu cam tiếp xúc ngoài với đường tròn màu xanh lá cây rỗng

c) Đồng hồ tiếp xúc trong với viền màu vàng rỗng kim loại

d) Đường tròn màu đỏ và đường tròn màu xanh da trời không giao nhau.

Bài 6 (trang 100)

Cho đường tròn (O; R) và dây AB khác đường kính. Gọi M là trung điểm của AB. 

a) Đường thẳng OM có phải là đường trung trực của đoạn thẳng AB hay không? Vì sao?

b) Tính khoảng cách từ điểm O đến đường thẳng AB. Biết R = 5 cm, AB = 8 cm.

Giải rút gọn:

a)

M là trung điểm AB ⇒ MA = MB (1)

OA = OB = R (2)

Từ (1) và (2) → OM là đường trung trực của đoạn thẳng AB

b) AM =

⇒ OM =

Bài 7 (trang 100)

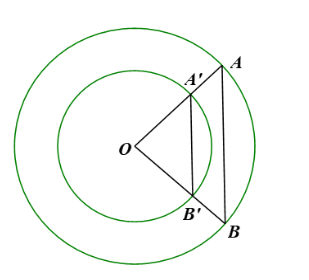
Cho hai đường tròn cùng tâm (O; R), (O; r) với R > r. Các điểm A, B thuộc đường tròn (O; R), các điểm A’, B’ thuộc đường tròn (O; r) sao cho O, A, A’ thẳng hàng; O, B, B’ thẳng hàng và điểm O không thuộc đường thẳng AB. Chứng minh:

a)

b) AB // A’B’.

Giải rút gọn:

a) 

⇒ (đpcm)

b) Xét :

Góc O chung

⇒  đồng dạng với nhau

Mà 2 góc này ở vị trí so le trong

AB // A’B’.