Siêu nhanh giải bài tập cuối chương VII toán 9 Cánh diều tập 2
Giải siêu nhanh bài tập cuối chương VII. Giải siêu nhanh Toán 9 Cánh diều tập 2. Những phần nào có thể rút gọn, lược bỏ và tóm gọn. Đều được áp dụng vào bài giải này. Thêm cách giải mới để học sinh lựa chọn. Để tìm ra phong cách học Toán 9 Cánh diều tập 2 phù hợp với mình
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI TẬP CUỐI CHƯƠNG 7
Bài 1 (trang 66):
Cho phương trình ![]() Điều kiện của c để phương trình có hai nghiệm phân biệt là
Điều kiện của c để phương trình có hai nghiệm phân biệt là
A.c < 1 B.c>1 C.c![]() D.c
D.c![]()
Giải rút gọn:
Chọn A
Bài 2 (trang 66):
Giả sử đồ thị hàm số y = a![]() là parabol ở hình 9. Giá trị của a bằng:
là parabol ở hình 9. Giá trị của a bằng:

A.2 B.-2 C.![]() D.
D.![]()
Giải rút gọn:
Chọn B
Bài 3 (trang 66):
Cho hàm số y= ![]()
a)Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

b)Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số.
Giải rút gọn:
a)
| x | 0 | 1 | 3 | ||
| y= | 0 |
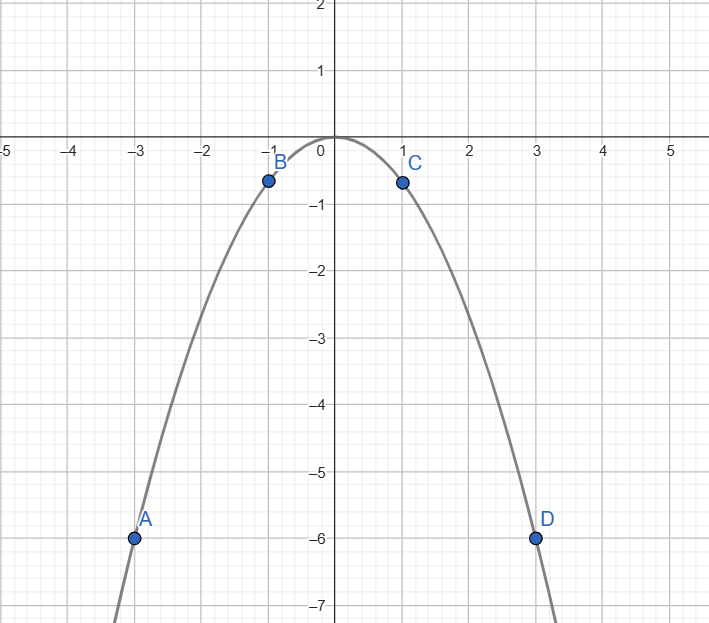
b)
A (![]() 3;
3;![]() 6)
6)
B (;)
O (0;0)
C (1;![]() )
)
D (3;![]() 6)
6)
Bài 4 (trang 66):
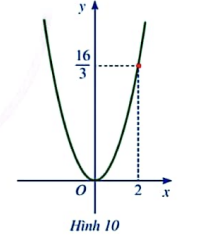
Trên mặt phẳng tọa độ Oxy, đường parabol ở hình 10 biểu diễn đồ thị hàm số y=a![]()
a)Tìm hệ số a
b)Tìm điểm thuộc đồ thị có hoành độ bằng 3
c)Tìm điểm thuộc đồ thị có tung độ bằng 4
Giải rút gọn:
a)Với x = 2, y = ![]() :
: ![]() =
=![]() ⇒ a =
⇒ a =![]()
Đồ thị hàm số có dạng y = ![]()
b)Với x = 3: y = ![]() = 12
= 12
Điểm cần tìm: (3;12)
c) Với y = 4: 4 = ![]()
⇒ x= ![]()
Điểm cần tìm: (![]() ;4) và (
;4) và (![]() ;4)
;4)
Bài 5 (trang 66):
Giải các phương trình:
a)![]()
b)![]()
c)![]()
Giải rút gọn:
a) Δ = 52 > 0
⇒ Phương trình có hai nghiệm phân biệt:
![]() =
= ![]() )
)
![]() =
= ![]() )
)
b) Δ = 0
⇒ Phương trình có nghiệm kép: ![]() =
= ![]()
c) Δ = ![]() < 0
< 0
⇒ Phương trình vô nghiệm.
Bài 6 (trang 66):
Không tính Δ, giải các phương trình
![]()
b)![]()
c)![]()
Giải rút gọn:
a) a = 1; b = - 3; c = 2
⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm: ![]() ;
; ![]()
b) a = - 3; b = 5; c = 8
⇒ a - b + c = 0
⇒ Phương trình có hai nghiệm: : ![]() ;
; ![]()
c)![]()
⇒ a + b + c = ![]()
⇒ Phương trình có nghiệm: ![]() ;
; ![]()
Bài 7 (trang 66):
Tìm hai số, biết tổng của chúng bằng 4![]() và tích của chúng bằng 6.
và tích của chúng bằng 6.
Giải rút gọn:
Hai số cần tìm là nghiệm phương trình:![]()
Δ =![]()
⇒ Phương trình có hai nghiệm phân biệt là: ![]() =
= ![]() ;
; ![]() =
= ![]()
Bài 8 (trang 67):
Giải thích vì sao nếu phương trình a![]() có hai nghiệm
có hai nghiệm ![]() ,
, ![]() thì
thì
a![]() =a(x -
=a(x - ![]() )(x -
)(x - ![]() ).
).
Áp dụng: phân tích các đa thức sau thành nhân tử
a) ![]()
b) 3![]()
Giải rút gọn:
a(x−![]() )(x−
)(x−![]() )=a[
)=a[![]() − (
− (![]() +
+![]() )x +
)x + ![]() ⋅
⋅![]() ] (1)
] (1)
Theo định lý Viète:
x1 + x2 ![]() ;
;
x1x2 = ![]() .
.
⇒ Thay vào (1) được: a![]()
a)![]()
Δ’ = 4 > 0
⇒ Phương trình có hai nghiệm phân biệt: ![]() ;
; ![]()
⇒ ![]() = 1.(x + 1)(x − 3)
= 1.(x + 1)(x − 3)
b) 3![]()
Δ = 49 > 0
⇒ Phương trình có hai nghiệm phân biệt: ![]() ;
; ![]()
⇒ ![]() = 3.(x + 2)(x −
= 3.(x + 2)(x − ![]() )
)
Bài 9 (trang 67):
Một chiếc áo có giá niêm yết là 120 000 đồng. Để thanh lý chiếc áo, đầu tiên người ta giảm giá x![]() so với giá niêm yết. Do vẫn chưa bán được chiếc áo nên người ta tiếp tục giảm giá x
so với giá niêm yết. Do vẫn chưa bán được chiếc áo nên người ta tiếp tục giảm giá x![]() so với giá vừa được giảm. Sau hai đợt giảm giá, giá của chiếc áo còn 76 800 đồng. Tìm x.
so với giá vừa được giảm. Sau hai đợt giảm giá, giá của chiếc áo còn 76 800 đồng. Tìm x.
Giải rút gọn:
ĐKXD: 0 < x < 100
Giá của chiếc áo sau đợt giảm đầu tiên: 120000(1 − ![]() )
)
Giá của chiếc áo sau 2 đợt giảm giá: 120000![]() = 76800
= 76800
⇒ x = 20
Vậy x = 20
Bài 10 (trang 67):
Một công ty sản xuất các khay có dạng hình hộp chữ nhật để trồng rau trong chung cư ở các thành phố. Biết diện tích mặt đáy của khay đó là 2 496 ![]() và chu vi mặt đáy của khay đó là 220cm. Tìm các kích thước mặt đáy của khay đó.
và chu vi mặt đáy của khay đó là 220cm. Tìm các kích thước mặt đáy của khay đó.
Giải rút gọn:
Hai kích thước cần tìm là nghiệm phương trình:![]()
⇒ x=32 và x=78
Vậy chiều dài của khay là 78cm, chiều rộng của khay là 32cm
Bài 11 (trang 67):
Cầu Trường Tiền (hay cầu Tràng Tiền) ở thành phố Huế được khởi công vào tháng 5/1899 và khánh thành vào ngày 18/12/1900. Cầu được thiết kế theo kiến trúc Gothic, bắc qua sông Hương. Từ Festival năm 2002, cầu Trường Tiền được lắp đặt một hệ thống chiếu sáng đổi màu hiện đại. Cầu dài 402,6m, gồm 6 nhịp dầm thép.
Giả sử một nhịp dầm thép có dạng parabol y=a![]() trong hệ trục tọa độ Oxy, ở đó Ox song song với mặt cầu. Biết rằng, hai chân nhịp dầm thép trên mặt cầu cách nhau 66,66m, khoảng cách từ đỉnh cao nhất của nhịp dầm thép đến mặt cầu là 5,54m (hình 11).
trong hệ trục tọa độ Oxy, ở đó Ox song song với mặt cầu. Biết rằng, hai chân nhịp dầm thép trên mặt cầu cách nhau 66,66m, khoảng cách từ đỉnh cao nhất của nhịp dầm thép đến mặt cầu là 5,54m (hình 11).
a)Xác định tọa độ của hai chân nhịp dầm trên.
b)Tìm a (làm tròn kết quả đến hàng phần nghìn)
Giải rút gọn:

a) Tọa độ chân nhịp dầm cầu bên trái: (-33,33;-5,45)
Tọa độ chân nhịp dầm cầu bên phải: (33,33;-5,45)
b) Với x = 33,33; y = - 5,45: - 5,45 = a.![]()
⇒ a= - 0,005
Đồ thị hàm số có dạng y = - 0,005![]()
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải Toán 9 Cánh diều tập 2 bài tập cuối chương VII, Giải bài tập cuối chương VII, Siêu nhanh giải bài tập cuối chương VII toán 9 Cánh diều tập 2
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận