CHƯƠNG II: BẤT ĐẲNG THỨC. BẤT PHƯƠNG TRÌNH MỘT ẨN

BÀI 1: BẤT ĐẲNG THỨC

Bài 1: Cho các số a, b, c, d đều khác 0 thoả mãn a > b và c > d Trong các bất đẳng thức sau, bất đẳng thức nào đúng?

a) a + c > b + d_

b) ac > bd

c) a - d > b - c

d) >

Giải chi tiết:

Bất đẳng thức ở các câu a,c là đúng

Bài 2: Cho a < b. So sánh:

a) M = -24(a + 23) và N = -24(b + 23)

b) P = a – 24 và Q = b

Giải chi tiết:

a)Do a < b nên a + 23 < b + 23 => -24(a + 23) > -24(b + 23)

Suy ra M > N

b)Do a < b nên a < b  => a – 24 < b – 23

Suy ra P < Q

Bài 3: Cho x, y là các số thực tuỳ ý thoả mãn x > y Bất đẳng thức x² > y² là đúng hay sai? Vì sao?

Giải chi tiết:

Bất đẳng thức x² > y² là sai

Chẳng hạn, chọn x = -1 và y = -2 ta có x² = 1 và y² = 4

Khi đó x > y nhưng x² < y²

Bài 4: Cho a, b, c, d là các số không âm thoả mãn a > c + d, b > c + d Chứng minh:

a) a + 2b > 3c + 3d

b) a² + b² > 2c² + 2cd + 2d²

c) ab > c² + cd + d²

Giải chi tiết:

Do a,b,c,d là các số không âm nên c + d cũng không âm.

Khi đó, với a > c + d, b > c + d ta có:

a)a + 2b > c + d + 2(c + d) hay a + 2b > 3c + 3d

b)a² + b² > (c + d)² + (c + d)² hay a² + b² > 2c² + 4cd + 2d²

Suy ra a² + b² > 2c² + 2cd + 2d² 

c)ab > (c + d)(c + d) hay ab > c² + 2cd + d²

Suy ra ab > c² + cd + d²

Bài 5: Cho x, y, z là các số thực tuỳ ý. Chứng minh:

a) x² + y² ≥ - 2xy

b) x² + y² + z² ≥ xy + yz + zx

c) 3(x² + y² + z²) ≥ (x + y + z)²

Giải chi tiết:

a)Với 2 số thực x, y tùy ý, ta có: (x + y)² ≥ 0 hay x² + 2xy + y² ≥ 0

Do đó x² + y² ≥ -2xy

b)Với 3 số thực x, y, z tùy ý, ta có: (x – y)² ≥ 0, (y – z)² ≥ 0, (z – x)² ≥ 0

hay (x – y)² + (y – z)² + (z – x)² ≥ 0

Suy ra x² – 2xy + y² + y² – 2yz + z² – 2zx + x² ≥ 0

Hay 2x² + 2y² + 2z² ≥ 2xy + 2yz + 2zx

Do đó x² + y² + z² ≥ xy + yz + zx

c)Xét hiệu: 3(x² + y² + z²) – (x + y + z)² = (x – y)² + (y – z)² + (z – x)²

Do (x – y)² + (y – z)² + (z – x)² ≥ 0 (theo câu b) nên 3(x² + y² + z²) – (x + y + z)² ≥ 0

Vậy 3(x² + y² + z²) ≥ (x + y + z)²

Bài 6: Chứng minh:

a)

b)

c)3.1024² > 2²¹

Giải chi tiết:

a)Ta có: 2 = . Do 5 < 6 và 7 > 4 nên < và >

Do đó - < - hay - < – 2

b) Do < và > nên - < -

Suy ra

c) Ta có: 2²¹ = 2.2²⁰ = 2. (2¹⁰)² = 2.1024²

Do 3 > 2 nên 3. 1024² > 2.1024²

Suy ra 3.1024² > 2²¹

Bài 7: Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh:

a) a² + b² + c² < 2(ab + bc + ca)

b)

Giải chi tiết:

a)Do a,b,c là độ dài ba cạnh của một tam giác nên a > 0, b > 0, c > 0, a + b > c, b + c > a, c + a > b

Suy ra a² < a(b + c), b² < b(c + a), c² < c(a + b)

Do đó a² + b² + c² < a(b + c) + b(c + a) + c(a + b)

Hay a² + b² + c² < 2(ab + bc + ca)

b)Theo kết quả Ví dụ 2c(trang 32), ta có:

Hay

Tương tự, ta chứng minh được

Do đó

Bài 8: Theo Tổng cục Môi trường, chỉ số chất lượng không khí được tính theo thang điểm (khoảng giá trị AQI) tương ứng với biểu tượng và màu sắc để cảnh báo chất lượng không khí và mức độ ảnh hưởng tới sức khoẻ con người, cụ thể như sau (Bảng 2):

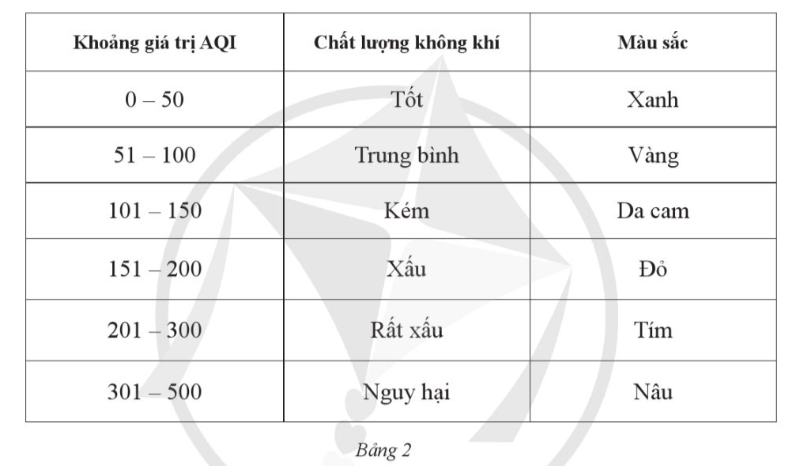
Chỉ số AQI tại Hà Nội, Thái Nguyên, Hưng Yên, Sơn La ghi nhận vào sáng ngày 09/01/2023 lần lượt là: 338; 406; 312,9; 78 (Nguồn: Tạp chí điện tử Môi trường và Cuộc sống). Dựa vào Bảng 2, cho biết chất lượng không khí vào sáng 09/01/2023 tại Hà Nội, Thái Nguyên, Hưng Yên, Sơn La ở mức nào trong các mức sau: Tốt, Trung bình, Kém, Xấu, Rất xấu, Nguy hại.

Giải chi tiết:

Chất lượng không khí vào sáng ngày 09/01/2023 tại Hà Nội, Thái Ngu Hưng Yên, Sơn La lần lượt ở mức Nguy hại, Nguy hại, Nguy hại, Trung bình

Bài 9: Một cửa hàng nhập về 60 chiếc điện thoại từ nước ngoài với giá nhập vào là 20 triệu đồng/chiếc. Thuế và phí vận chuyển của 60 chiếc điện thoại đó lần lượt là 36 triệu đồng và 20 triệu đồng. Khi về Việt Nam, cửa hàng đó đã bán mỗi chiếc điện thoại với giá bán bằng 125% giá nhập vào. Nhận định “Sau khi bán hết 60 chiếc điện thoại đó, cửa hàng đã lãi hơn 250 triệu đồng” là đúng hay sai?Vi sao?

Giải chi tiết:

Số tiền lãi mà cửa hàng đó thu được khi bán hết 60 chiếc điện thoại đó là: 

      ( 125%.20.60) - (20.6 + 36 + 20) = 244 (triệu đồng). 

Do 244 < 250 nên nhận định đã cho là sai.

Bài 10: Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn 

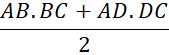
Giải chi tiết:

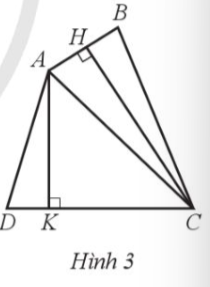
Kẻ CH vuông góc với ABtaiH AK vuông góc với DC tại K (Hình 3). 

Khi đó, diện tích của tam giác ABC là: 

S₁ =

và diện tích của tam giác ACD là:

 S₂ =

Diện tích của tứ giác ABCD là: 

S = S₁ + S₂ =

Mà CH ≤ BC và AK ≤ AD suy ra 

S

Vậy diện tích của tứ giác ABCD không lớn hơn

Bài 11*: Bác Long dùng 80 m lưới thép gai để rào một mảnh vườn có dạng hình chữ nhật. Bác Long đã tận dụng bờ giậu có sẵn để làm một cạnh hàng rào của mảnh vườn. Tìm các kích thước của mảnh vườn có diện tích lớn nhất mà bác Long rào được bằng 80 m lưới thép gai

Giải chi tiết:

Gọi x (m) là độ dài cạnh song song với bờ giậu và y (m) là độ dài cạnh vuông góc với bờ giậu (x > 0, y > 0) Khi đó, ta có: x + 2y = 80 hay x = 80 - 2y

Diện tích của mảnh vườn là: 

S = xy = (80 - 2y) y = - 2y² + 80y = - 20(y² - 40y + 400 ) + 800 

   = - 2(y - 20)² + 800 (m²) .

Do (y - 20)² ≥ 0 với số y tuỳ ý nên - 2(y - 20)² + 800 ≤ 800 

Do đó, diện tích lớn nhất của mảnh vườn mà bác Long rào được là 800m²

Dấu “=” xảy ra khi y - 20 = 0 hay y = 20 

Thay y = 20 vào x = 80 - 2y ta được: x = 80-2.20=40. 

Vậy mảnh vườn có diện tích lớn nhất mà bác Long rào được có chiều dài 40 m và chiều rộng 20 m