Giải VBT Toán 9 Cánh diều bài 1: Hàm số y=ax^2 (a ≠ 0)
Giải chi tiết VBT Toán 9 cánh diều bài 1: Hàm số y=ax^2 (a ≠ 0). Tech12h sẽ hướng dẫn giải tất cả câu hỏi và bài tập với cách giải nhanh và dễ hiểu nhất. Hi vọng, thông qua đó học sinh được củng cố kiến thức và nắm bài học tốt hơn.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Chương VII: HÀM SỐ ![]() . PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
. PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
BÀI 1: HÀM SỐ ![]() .
.
Bài 1 (trang 57):
Diện tích toàn phần của hình lập phương cạnh ![]() được cho bởi công thức
được cho bởi công thức ![]() .
.
a) Tính các giá trị của ![]() rồi hoàn thiện bảng sau:
rồi hoàn thiện bảng sau:
| 2 | 2,7 | 1,22 | 0,001 |
|
|
|
|
|
b) Tính cạnh ![]() của hình lập phương (theo đơn vị centimét và làm tròn kết quả đến hàng phần trăm), biết diện tích toàn phần của hình lập phương đó bằng
của hình lập phương (theo đơn vị centimét và làm tròn kết quả đến hàng phần trăm), biết diện tích toàn phần của hình lập phương đó bằng ![]() .
.
Bài giải chi tiết:
a)
| 2 | 2,7 | 1,22 | 0,001 |
| 24 | 43,74 | 8,9304 | 0,000006 |
b) Công thức diện tích toàn phần của hình lập phương:
![]()
![]()
![]()
Bài 2 (trang 57):
Cho hàm số ![]() . Tìm
. Tìm ![]() , biết khi
, biết khi ![]() thì
thì ![]() .
.
Bài giải chi tiết:
Ta có ![]() và
và ![]()
![]()
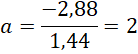
Bài 3 (trang 57):
Galileo Galilei là người phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian. Liên hệ giữa quãng đường chuyển động ![]() (mét) và thời gian chuyến động
(mét) và thời gian chuyến động ![]() (giây) được cho bởi hàm số
(giây) được cho bởi hàm số ![]() . Người ta thả một vật nặng từ độ cao
. Người ta thả một vật nặng từ độ cao ![]() trên tháp nghiêng Pi-sa xuống đất (sức cản của không khí không đáng kể).
trên tháp nghiêng Pi-sa xuống đất (sức cản của không khí không đáng kể).
a) Hỏi sau thời gian 2,5 giây vật nặng còn cách mặt đất bao nhiêu mét?
b) Khi vật nặng còn cách mặt đất ![]() thì nó đã rơi thời gian bao nhiêu giây?
thì nó đã rơi thời gian bao nhiêu giây?
Bài giải chi tiết:
a) Sau thời gian 2,5 giây vật nặng còn cách mặt đất:
![]()
b) Quãng đường vật nặng đi được khi vật nặng còn cách mặt đất ![]() là
là
![]()
Thời gian vật nặng đi được quãng đường ![]() là
là

Bài 4 (trang 57):
Một viên bi lăn trên mặt phẳng nghiêng. Đoạn đường đi được liên hệ với thời gian bởi hàm số ![]() (
( ![]() tính bằng giây,
tính bằng giây, ![]() tính bằng mét). Người ta đo được quãng đường viên bi lăn được ở thời điểm 3 giây là
tính bằng mét). Người ta đo được quãng đường viên bi lăn được ở thời điểm 3 giây là ![]() . Hỏi khi viên bi lăn được quãng đường
. Hỏi khi viên bi lăn được quãng đường ![]() thì nó đã lăn trong bao lâu?
thì nó đã lăn trong bao lâu?
Bài giải chi tiết:
Với ![]() ta có
ta có
![]()
Với ![]() ta có
ta có
![]()
Thay ![]() vào (1) ta được
vào (1) ta được
![]()
Từ (2) và ![]() , ta có
, ta có ![]() . Vậy khi viên bi lăn được
. Vậy khi viên bi lăn được ![]() thì nó đã lăn trong 5 giây.
thì nó đã lăn trong 5 giây.
Bài 5 (trang 57):
a) Điểm ![]() thuộc đồ thị hàm số nào trong các hàm số sau:
thuộc đồ thị hàm số nào trong các hàm số sau: ![]() ;
; ![]()
b) Trong các điểm ![]() , điểm nào thuộc đồ thị hàm số
, điểm nào thuộc đồ thị hàm số ![]() ?
?
Bài giải chi tiết:
a) ![]() thuộc đồ thị hàm số
thuộc đồ thị hàm số ![]() .
.
b) ![]() thuộc đồ thị hàm số
thuộc đồ thị hàm số ![]() .
.
Bài 6 (trang 58):
Cho ![]() là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng ![]() và
và ![]() . Chứng minh rằng điểm
. Chứng minh rằng điểm ![]() thuộc đồ thị hàm số
thuộc đồ thị hàm số ![]() .
.
Bài giải chi tiết:
Do ![]() là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng ![]() và
và ![]()
![]()
![]()
![]()
Suy ra ![]() . Mặt khác
. Mặt khác ![]() nên
nên ![]() thuộc đồ thị hàm số
thuộc đồ thị hàm số ![]() .
.
Bài 7 (trang 58):
Cho hàm số ![]() có đồ thị là một parabol với đỉnh
có đồ thị là một parabol với đỉnh ![]() như Hình 3.
như Hình 3.
a) Tìm giá trị của ![]() .
.
b) Tìm tung độ của điểm thuộc parabol có hoành độ bằng 2 .
c) Tìm các điểm thuộc parabol có tung độ bằng 2 .![]() ) Tìm các điểm (không phải điểm
) Tìm các điểm (không phải điểm ![]() ) thuộc parabol sao cho khoảng cách từ điểm đó đến trục hoành gấp ba lần khoảng cách từ điểm đó đến trục tung.
) thuộc parabol sao cho khoảng cách từ điểm đó đến trục hoành gấp ba lần khoảng cách từ điểm đó đến trục tung.
Bài giải chi tiết:
a) Do đồ thị hàm số đi qua ![]() nên
nên ![]() . Vậy
. Vậy ![]() .
.
b) Tung độ của điểm thuộc parabol có hoành độ bằng 2 là: ![]() .
.
c) Ta có ![]() nên
nên ![]() hoặc
hoặc ![]() . Vậy các điểm thuộc parabol có tung độ bằng 2 là
. Vậy các điểm thuộc parabol có tung độ bằng 2 là ![]() .
.
![]() Gọi
Gọi ![]() là điểm thuộc parabol thỏa mãn khoảng cách từ điểm đó đến trục hoành gấp ba lần khoảng cách từ điểm đó đến trục tung.
là điểm thuộc parabol thỏa mãn khoảng cách từ điểm đó đến trục hoành gấp ba lần khoảng cách từ điểm đó đến trục tung.
Từ đó, ta có ![]() và
và ![]() . Do
. Do ![]() nên
nên ![]() hoặc
hoặc ![]() .
.
Nếu
 , kết hợp với (*) ta có:
, kết hợp với (*) ta có: 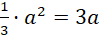 hay
hay  . Suy ra
. Suy ra 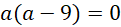 . Tức là
. Tức là 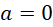 hoặc
hoặc 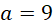 . Với
. Với  thì
thì 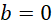 , khi đó
, khi đó 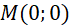 (loại). Với
(loại). Với 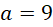 thì
thì 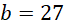 , khi đó
, khi đó 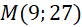 .
.Nếu
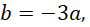 kết hợp với (*) ta có:
kết hợp với (*) ta có: 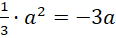 hay
hay 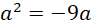 . Suy ra
. Suy ra 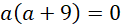 . Tức là
. Tức là  hoặc
hoặc  . Với
. Với 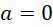 thì
thì 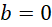 , khi đó
, khi đó 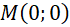 (loại). Với
(loại). Với 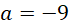 thì
thì 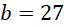 , khi đó
, khi đó 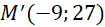 .
.
Vậy các điểm phải tìm là ![]() và
và ![]() .
.
Bài 8 (trang 58):
Nước từ một vòi nước (đặt trên mặt nước) được phun lên cao sẽ đạt đến một độ cao nào đó rồi rơi xuống (Hình 4). Giả sử nước được phun ra bắt đầu từ vị trí ![]() trên mặt nước và rơi trở lại mặt nước ở vị trí
trên mặt nước và rơi trở lại mặt nước ở vị trí ![]() , đường đi của nước có dạng một phần của parabol
, đường đi của nước có dạng một phần của parabol ![]() trong hệ trục toạ độ
trong hệ trục toạ độ ![]() , với gốc tọa độ
, với gốc tọa độ ![]() là vị trí cao nhất mà nước được phun ra đạt được so với mặt nước, trục
là vị trí cao nhất mà nước được phun ra đạt được so với mặt nước, trục ![]() song song với
song song với ![]() và
và ![]() được tính theo đơn vị mét. Tính chiều cao
được tính theo đơn vị mét. Tính chiều cao ![]() từ điểm
từ điểm ![]() đến mặt nước, biết khoảng cách giữa điểm
đến mặt nước, biết khoảng cách giữa điểm ![]() và điểm
và điểm ![]() là
là ![]() .
.
Bài giải chi tiết:
Gọi ![]() là trung điểm của đoạn
là trung điểm của đoạn ![]() . Khi đó
. Khi đó ![]() và
và ![]() .
.
Từ đó, trong hệ trục ![]() , hoành độ của
, hoành độ của ![]() bằng 3 , tung độ của
bằng 3 , tung độ của ![]() bằng
bằng ![]() .
.
Do đó: ![]() , suy ra
, suy ra ![]() .
.
Bài 9 (trang 59):
Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng một phần của parabol ![]() với gốc tọa độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét, chiều cao OK của cổng là 4,5 m như mô tả ở Hình 5 (K là trung điểm của đoạn AB). Tìm khoảng cách giữa hai chân cổng A và B ở trên mặt đất.
với gốc tọa độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét, chiều cao OK của cổng là 4,5 m như mô tả ở Hình 5 (K là trung điểm của đoạn AB). Tìm khoảng cách giữa hai chân cổng A và B ở trên mặt đất.
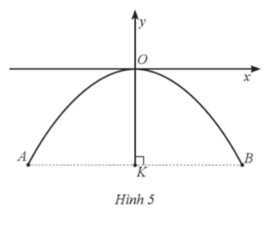
Bài giải chi tiết:
Từ Hình 5, ta có K(0;–4,5).
Gọi hoành độ của điểm B là b (b > 0).
Do tung độ của điểm B bằng tung độ của K nên B(b;–4,5).
Mặt khác, B thuộc parabol ![]() nên ta có:
nên ta có: ![]()
hay ![]() = 36, nên b = 6 (do b > 0).
= 36, nên b = 6 (do b > 0).
Từ đó KB = 6 m và AB=2.KB = 2.6 = 12 m.
Vậy khoảng cách giữa hai chân cổng A và B ở trên mặt đất bằng 12 mét.
Bài 10 (trang 10):
a) Vẽ đồ thị các hàm số ![]() và
và ![]() trên cùng một mặt phẳng toạ độ Oxy.
trên cùng một mặt phẳng toạ độ Oxy.
b) Qua đồ thị của các hàm số đó, hãy cho biết khi x tăng từ 0,5 đến 2 thì giá trị lớn nhất của hàm số ![]() và giá trị nhỏ nhất của hàm số
và giá trị nhỏ nhất của hàm số ![]() là bao nhiêu?
là bao nhiêu?
Bài giải chi tiết:
a) – Vẽ đồ thị hàm số: ![]()
Ta có bảng giá trị của y tương ứng với giá trị của t như sau:
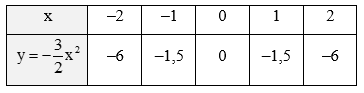
- Vẽ các điểm A(‒2; ‒6); B (‒1; ‒1,5); O(0; 0); C(1; ‒1,5); D(2; ‒6) thuộc đồ thị hàm số ![]() trong mặt phẳng tọa độ Oxy.
trong mặt phẳng tọa độ Oxy.
- Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số ![]() (hình vẽ).
(hình vẽ).
– Vẽ đồ thị hàm số ![]()
Ta có bảng giá trị của y tương ứng với giá trị của t như sau:

- Vẽ các điểm M(‒2; 6); N(‒1; 1,5); O(0; 0); P(1; 1,5); Q(2; 6) thuộc đồ thị hàm số ![]() trong mặt phẳng tọa độ Oxy.
trong mặt phẳng tọa độ Oxy.
- Vẽ đường parabol đi qua 5 điểm M, N, O, P, Q, ta nhận được đồ thị của hàm số ![]() (hình vẽ).
(hình vẽ).
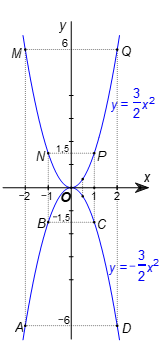
b) Từ đồ thị hàm số ở câu a, ta thấy khi x tăng từ 0,5 đến 2 thì hàm số ![]() có giá trị lớn nhất bằng tại x = 0,5 và hàm số
có giá trị lớn nhất bằng tại x = 0,5 và hàm số ![]() có giá trị nhỏ nhất tại x = 0,5.
có giá trị nhỏ nhất tại x = 0,5.
Thay x = 0,5 vào hàm số ![]() ta được:
ta được:
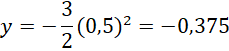
Thay x = 0,5 vào hàm số![]() ta được:
ta được:
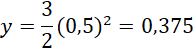
Vậy khi x tăng từ 0,5 đến 2 thì hàm số ![]() có giá trị lớn nhất bằng ‒0,375 tại x = 0,5 và hàm số
có giá trị lớn nhất bằng ‒0,375 tại x = 0,5 và hàm số ![]() có giá trị nhỏ nhất bằng 0,375 tại x = 0,5.
có giá trị nhỏ nhất bằng 0,375 tại x = 0,5.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải VBT Toán 9 cánh diều , Giải VBT Toán 9 CD, Giải VBT Toán 9 bài 1: Hàm số y=ax^2 (a ≠ 0)
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận