BÀI 2: PHƯƠNG TRÌNH BẬC 2 MỘT ẨN

Bài 11 (trang 64):

Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn? Đối với những phương trình bậc hai một ẩn đó, xác định hệ số của , hệ số của , hệ số tự do .
a) .
b) .
c) .
d) .
e) .
g) .

Bài giải chi tiết:

Các phương trình b) và d) là các phương trình bậc hai một ẩn.

 Ở phương trình b ), ta có . 

Ở phương trình ), ta có .
Bài 12 (trang 64):

Tìm các giá trị của để phương trình là phương trình bậc hai một ẩn.

Bài giải chi tiết:

Để phương trình là bậc 2 một ẩn, ta có:

và .
Bài 13 (trang 65): Giải các phương trình:
a) ;
b) ;
c) ;
d) ;
e) ;
g) .

Bài giải chi tiết:

a)

b)

Do là số âm, phương trình không có nghiệm thực.
Vậy phương trình không có nghiệm thực.

c)

vì là số dương, phương trình có hai nghiệm thực:

d) Phương trình:

Ta có:

Vì là số dương, phương trình có hai nghiệm thực:

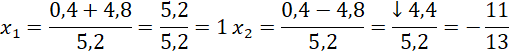
e) Phương trình:

Phương trình này sẽ có hai nghiệm:

g) Phương trình:

Ta có:

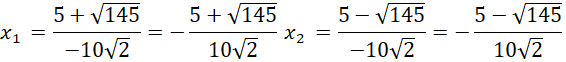
Bài 14 (trang 65):  Tìm các giá trị của để phương trình vô nghiệm.

Bài giải chi tiết:

Để phương trình vô nghiệm, ta có:

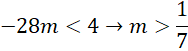
Bài 15 (trang 65):

Ở một gian hàng của siêu thị, người ta xếp các khối hàng hình lập phương giống nhau thành hình tháp tầng, với  tầng đáy thứ có khối hàng, tầng ngay trên tầng đáy có khối hàng, . tầng trên cùng có 1 khối hàng (chẳng hạn với ta có cách xếp như minh hoạ ở Hình 7).
a) Tính tổng số các khối hàng đã xếp ở một hình tháp tầng.
b) Tìm , biết .

Bài giải chi tiết:

a) Tổng số các khối hàng ở một hình tháp tầng là:

b) Ta có: , suy ra: 

Do là số dương, phương trình có hai nghiệm thực:

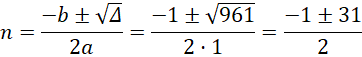
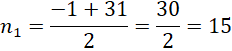
 Phương trình đã cho có hai nghiệm phân biệt là: (thoả mãn) và (không thoả mãn).

Bài 16 (trang 65):

Một chiếc ô tô đang chạy thì bắt đầu tăng tốc. Quãng đường đi được của chiếc ô tô đó kể từ khi bắt đầu tăng tốc được tính theo công thức: ( tính bằng mét, tính bằng giây, ).
a) Tính quãng đường ô tô đó đi được sau 7 giây kể từ khi bắt đầu tăng tốc.
b) Ô tô đó mất bao lâu để đi được quãng đường kể từ khi bắt đầu tăng tốc?

Bài giải chi tiết:

a) Quãng đường ô tô đi được sau 7s:

b) Ta có s=80:

Do là số dương, phương trình có hai nghiệm thực:

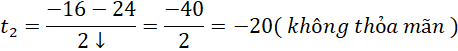
Vậy ô tô cần di chuyển với thời gian 4s để đi được 80m.

Bài 17 (trang 65):

Doanh thu (nghìn đồng) từ tiền bán vé trong ngày 1 tháng 6 của một rạp chiếu phim với giá mỗi vé là (nghìn đồng) được tính theo công thức: . Xác định giá vé bán trong ngày 1 tháng 6 của rạp chiếu phim đó, biết doanh thu từ tiền bán vé của ngày hôm đó là 12249 nghìn đồng.

Bài giải chi tiết:

Ta có doanh thu 1 ngày T=12249 nghìn đồng:

Do là số dương, phương trình có hai nghiệm thực:

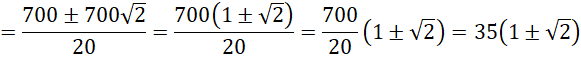
Vậy cần bán vé với giá 35 nghìn đồng để có doanh thu đã cho.

Bài 18 (trang 65):

Một kilôgam thịt lợn có giá bán ban đầu là 100 nghìn đồng. Vào dịp Tết Nguyên Đán, người ta tăng giá thêm so với giá bán ban đầu. Sau Tết Nguyên Đán do nguồn cung khan hiếm nên người ta tiếp tục tăng giá thêm so với giá đã tăng. Sau hai đợt tăng giá, giá của một kilôgam thịt lợn là 108 nghìn đồng. Tìm (làm tròn đến hàng đơn vị).

Bài giải chi tiết:

Sau lần tăng giá đầu tiên, giá mới là:

Sau lần tăng giá thứ hai, giá mới là:

Theo đề bài, sau hai đợt tăng giá, giá của một kilôgam thịt lợn là 108 nghìn đồng. Vậy ta có phương trình:

Ta có:

Vậy phương trình có hai nghiệm:

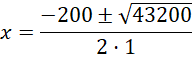
Vậy x=4

Bài 19 (trang 66):

Một công ty dự định thuê một số xe lớn (cùng loại) để chở hết 210 người đi du lịch Hội An. Nhưng thực tế, công ty lại thuê các xe nhỏ hơn (cùng loại). Biết rằng số xe nhỏ phải thuê nhiều hơn số xe lớn là 2 chiếc thì mới chở hết số người trên và mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người. Tìm số xe nhỏ đã thuê.

Bài giải chi tiết:

Gọi số xe lớn công ty dự định thuê là , đơn vị: chiếc ) thì số xe nhỏ công ty thuê là (chiếc). 

Mỗi xe lớn công ty dự định thuê chở số người là (người). 

Mỗi xe nhỏ chở số người là (người).

 Mỗi xe nhỏ chở ít hơn mỗi xe lớn là 12 người nên ta có phương trình:

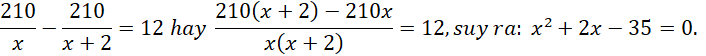
Ta có:

Số xe nhỏ cho thuê:

Vậy số xe nhỏ công ty đã thuê là 7 chiếc.
Bài 20 (trang 66):

Một hộp quà thiết kế theo dạng hình hộp chữ nhật. Bốn mặt thân hộp là các hình chữ nhật may bằng vải màu đỏ có chiều dài , hai đáy hộp là các hình vuông cạnh may bằng vải màu xanh (xem Hình 8 ). Tìm để tổng diện tích vải màu đỏ nhiều hơn ba lần tổng diện tích vải màu xanh là , biết .

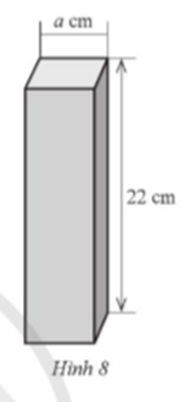
Bài giải chi tiết:

Tổng diện tích vải màu đỏ: .

Tổng diện tích vải màu xanh: .

Tổng diện tích vải màu đỏ nhiều hơn ba lần tổng diện tích vải màu xanh là . Tức là .

Ta có:                                                                                        

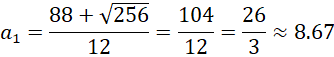
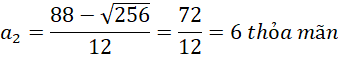
Vậy a = 6.

Bài 21 (trang 66):

a) Lập công thức tính diện tích xung quanh của một hình chóp tam giác đều, biết độ dài
Hinh 8 cạnh đáy là và độ dài trung đoạn là .
b) Tìm để diện tích xung quanh của hình chóp tam giác đều đó là .

Bài giải chi tiết:

a) Công thức tính diện tích xung quanh hình chóp tam giác đều:

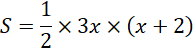
b) Ta có S =

Giải nghiệm:

Vì phải là chiều dài dương, nên ta chọn .
Vậy, để diện tích xung quanh của hình chóp tam giác đều là , thì phải là .

Bài 22 (trang 66):

Bác Na dùng rào dây thép gai đế rào một mành đất đủ rộng thành một mảnh vườn hình chữ nhật.
a) Lập công thức tính diện tích của mảnh vườn hình chữ nhật rào được theo chiều rộng của mảnh vườn đó.
b) Tìm diện tích lớn nhất có thể rào được của mảnh vườn hình chữ nhật đó.

Bài giải chi tiết: 

a) Đặt chiều rộng của mảnh vườn là mét, chiều dài là mét.

Chu vi của mảnh vườn là:

Diện tích của mảnh vườn là:

Bác dùng dây thép gai, tức là:

Từ đây suy ra:

Vậy, công thức diện tích của mảnh vườn hình chữ nhật là:

b) Ta có  

đạt giá trị lớn nhất bằng 2500 khi x = 50. Vậy diện tích lớn nhất của mảnh vườn có thể rào được là 2500 mét vuông.

Bài 23 (trang 66):

Người ta lát đá và trồng cỏ cho một sân chơi. Sân có dạng hình chữ nhật với các kích thước . Người ta đã dùng 1000 viên đá lát hình vuông cạnh để lát, diện tích còn lại để trồng cỏ. Tìm , biết chi phí để trồng cỏ là 4480000 đồng và giá trồng mỗi mét vuông cỏ là 35000 đồng.

Bài giải chi tiết:

Diện tích sân chơi:

Diện tích cỏ cần trồng:

Giá mỗi mét vuông cỏ là 35000 đồng và chi phí là 4480000 đồng:

Ta có:

Giải phương trình:

Vì , nên ta chọn .