BÀI 4: PHÉP THỬ NGẪU NHIÊN VÀ KHÔNG GIAN MẪU. XÁC SUẤT CỦA BIẾN CỐ

Bài 24 (trang 35):

Một hộp có 30 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số ; hai thẻ khác nhau thì ghi hai số khác nhau. Xét phép thử "Rút ngẫu nhiên một thẻ trong hộp".
a) Liệt kê các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
b) Tính xác suất của mỗi biến cố sau:
: "Số xuất hiện trên thẻ được rút ra lớn hơn 12 và là ước của 60 ";
: "Số xuất hiện trên thẻ được rút ra lớn hơn 2 và chia cho 8 dư 2 ";
: "Số xuất hiện trên thẻ được rút ra chia hết cho cả 3 và 5 ".

Bài giải chi tiết:

a) Các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là: ; .
b)

Các số xuất hiện trên thẻ được rút ra lớn hơn 12 và là ước của 60 là: 20; 30; 60 .
Vậy .

Các số xuất hiện trên thẻ được rút ra chia cho 8 dư 2 là: ; 50; 58. Vậy .

Các số xuất hiện trên thẻ được rút ra là số chia hết cho cả 3 và 5 là: 30 ; 60 . Vậy .

Bài 25 (trang 35):

Viết ngẫu nhiên một số tự nhiên có hai chữ số không nhỏ hơn 80 .
a) Viết tập hợp gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra.
b) Tính xác suất của mỗi biến cố sau:
: "Số tự nhiên được viết ra có chữ số hàng chục lớn hơn chữ số hàng đơn vị";
: "Số tự nhiên được viết ra có chữ số hàng chục gấp hai hoặc gấp ba lần chữ số hàng đơn vị".

Bài giải chi tiết:

a) .
b) - Số tự nhiên được viết ra có chữ số hàng chục lớn hơn chữ số hàng đơn vị là: . Vậy .

Số tự nhiên được viết ra có chữ số hàng chục gấp hai hoặc gấp ba lần chữ số hàng đơn vị là: . Vậy .

Bài 26 (trang 36):

Viết ngẫu nhiên một số tự nhiên có ba chữ số nhỏ hơn 400 .
a) Tính số phần tử của tập hợp gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra.
b) Tính xác suất của mỗi biến cố sau:
A: "Số tự nhiên được viết ra là lập phương của một số tự nhiên";
B: "Số tự nhiên được viết ra là số tự nhiên nhỏ nhất và khi chia số đó cho có số dư lần lượt là ".

Bài giải chi tiết:

a) . Vậy số phần tử của là 300 .
b) - Số tự nhiên được viết ra là lập phương của một số tự nhiên là: 125; 216; 343 .
Vậy .

Gọi số tự nhiên phải tìm là , theo đề bài ta có . Do chia cho 5 có số dư là 3 nên chia hết cho 5 . Tương tự chia hết cho 6 và chia hết cho 7 hay chia hết cho . Do đó, ta có . Mặt khác, và nên . Suy ra . Vậy .

Bài 27 (trang 36):

Một đội học sinh gồm 7 bạn tham gia cuộc thi "An toàn giao thông cho học sinh trung học cơ sở" do nhà trường tổ chức. Trong đó có 5 bạn học sinh lớp 9 là: An (lớp 9A), Bình (lớp ), Bảo (lớp ), Bách (lớp 9D), Lâm (lớp 9E) và 4 bạn học sinh lớp 8 là: Minh (lớp 8A), Hà (lớp 8B), Ngọc (lớp 8 C), Lan (lớp 8E). Chọn ngẫu nhiên một thí sinh trong đội học sinh tham gia cuộc thi đó.
a) Liệt kê các cách chọn có thể thực hiện được. Có tất cả bao nhiêu kết quả có thể xảy ra?
b) Tính xác suất của mỗi biến cố sau:
A: "Thí sinh được chọn là học sinh lớp 8 ";
: "Thí sinh được chọn là học sinh lớp ".

Bài giải chi tiết:

a) Các cách chọn một thí sinh có thể thực hiện được là: An (lớp ); Bình (lớp 9A); Bảo (lớp 9B); Bách (lớp 9D); Lâm (lớp 9E); Minh (lớp 8A); Hà (lớp 8B); Ngọc (lớp 8C); Lan (Lớp ). Do đó có tất cả 9 kết quả có thể xảy ra.

b) Các thí sinh lớp 8 có thể được chọn ra là: Minh (lớp ); Hà (lớp ); Ngọc (lớp ); Lan (lớp ). Vậy .

Các thí sinh lớp có thể được chọn ra là An (lớp ); Bình (lớp ). Vậy .

Bài 28 (trang 36):

Một trường trung học cơ sở có 2 học sinh nam và 2 học sinh nữ đạt giải cuộc thi viết thư quốc tế UPU. Bốn bạn học sinh đó được xếp ngẫu nhiên thành một hàng ngang để nhận phần thưởng. Tính xác suất của biến cố : " 2 học sinh nữ được xếp không đứng cạnh nhau".

Bài giải chi tiết:

Có 2 học sinh nam và 2 học sinh nữ xếp thành hàng ngang; do đó có 24 cách sắp xếp (1). Gọi hai học sinh nam là và 2 học sinh nữ là . 

Ta có 12 cách xếp để hai học sinh nữ đứng cạnh nhau đó là: ; BDCA; ABCD; ABDC; BACD; BADC; CDAB; CDBA; DCAB; DCBA (2). 

Từ (1) và (2) ta có số cách xếp sao cho 2 học sinh nữ không đứng cạnh nhau là: (cách). 

Do đó có 12 kết quả thuận lợi cho biến cố . Vậy xác suất của biến cố : "2 học sinh nữ được xếp không đứng cạnh nhau" là: .

Bài 29 (trang 36):

Một hộp có chứa ba viên bi vàng lần lượt ghi các số và hai viên bi nâu lần lượt ghi các số 4 ; 5 . Lấy ngẫu nhiên đồng thời hai viên bi trong hộp. Tính xác suất của mỗi biến cố sau:
A: "Hai viên bi được lấy ra cùng màu vàng";
: "Hai viên bi được lấy ra khác màu".

Bài giải chi tiết:

Do đó, tập hợp có 10 phần tử.

Các khả năng để hai viên bi được lấy ra cùng màu vàng là: . Vậy .

Các khả năng để hai viên bi được lấy ra khác màu là: ; . Vậy .

Bài 30 (trang 36):

Một hộp có chứa 15 quả cầu màu xanh được đánh số từ 1 đến 15 và 5 quả cầu màu đỏ được đánh số từ 16 đến 20 . Lấy ngẫu nhiên một quả trong hộp. Tính xác suất của mỗi biến cố sau:
a) "Quả cầu được lấy ra có màu xanh";

b) "Quả cầu được lấy ra ghi số chẵn";
c) "Quả cầu được lấy ra có màu xanh và ghi số lẻ chia cho 3 dư 1";
d) "Quả cầu được lấy ra có màu đỏ hoặc ghi số chẵn".

Bài giải chi tiết:

a) Xác suất của biến cố "Quả cầu được lấy ra có màu xanh"

- Số quả cầu màu xanh: 15

- Tổng số quả cầu: 20

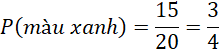
 b) Xác suất của biến cố "Quả cầu được lấy ra ghi số chẵn"

- Các quả cầu ghi số chẵn: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20

- Số quả cầu ghi số chẵn: 10

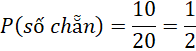
c) Xác suất của biến cố "Quả cầu được lấy ra có màu xanh và ghi số lẻ chia cho 3 dư 1".

- Các số lẻ chia cho 3 dư 1 trong khoảng từ 1 đến 15 là: 1, 7, 13

- Số quả cầu màu xanh ghi số 1, 7, 13: 3

d) Xác suất của biến cố "Quả cầu được lấy ra có màu đỏ hoặc ghi số chẵn"

- Số quả cầu màu đỏ: 5

- Số quả cầu ghi số chẵn: 10

- Các quả cầu màu đỏ và ghi số chẵn không trùng lặp, vì các quả cầu màu đỏ được đánh số từ 16 đến 20, trong đó có 3 số chẵn (16, 18, 20).

Vì vậy, tổng số quả cầu có màu đỏ hoặc ghi số chẵn là:

 5 (màu đỏ) + 7 (số chẵn không phải màu đỏ) = 10 

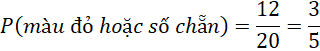
Bài 31 (trang 37):

 Đối với nhiều quốc gia, cảng biển có vai trò hết sức quan trọng trong phát triển kinh tế của đất nước. Đó là cửa ngõ giao thương hàng hoá xuất, nhập khẩu. 13 cảng biển lớn trên thế giới đã được lựa chọn trong danh sách sau: Thượng Hải (thuộc Trung Quốc), Singapore (thuộc Singapore), Busan (thuộc Hàn Quốc), Hải Phòng (thuộc Việt Nam), Durban (thuộc Nam Phi), Lagos (thuộc Nigeria), Container Kênh Suez (thuộc Ai Cập), Kenya Mombasa (thuộc Kenya), Rotterdam (thuộc Hà Lan), Antwerp (thuộc Bi), Hamburg (thuộc Đức), Valencia (thuộc Tây Ban Nha), Piraeus (thuộc Hy Lạp); mỗi nước chỉ có đúng một cảng biển được chọn. Chọn ngẫu nhiên một cảng biển trong 13 cảng biển đó.
a) Viết tập hợp gồm các kết quả có thể xảy ra đối với cảng biển được chọn. Tính số phần tử của tập hợp .
b) Tính xác suất của mỗi biến cố sau:
A: "Cảng biển được chọn thuộc châu Á";
: "Cảng biển được chọn thuộc châu Âu";
C: "Cảng biển được chọn thuộc châu Phi".

Bài giải chi tiết:

a) 

Số phần tử của tập hợp là:

 b) Tính xác suất của các biến cố

Biến cố A: "Cảng biển được chọn thuộc châu Á"

Các cảng biển thuộc châu Á là:

- Thượng Hải (thuộc Trung Quốc)

- Singapore (thuộc Singapore)

- Busan (thuộc Hàn Quốc)

- Hải Phòng (thuộc Việt Nam)

Do đó, số phần tử của tập hợp con A là:

 |A| = 4 

Xác suất của biến cố A là:

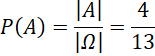
Biến cố B: "Cảng biển được chọn thuộc châu Âu"

Các cảng biển thuộc châu Âu là:

- Rotterdam (thuộc Hà Lan)

- Antwerp (thuộc Bỉ)

- Hamburg (thuộc Đức)

- Valencia (thuộc Tây Ban Nha)

- Piraeus (thuộc Hy Lạp)

Do đó, số phần tử của tập hợp con B là:

 |B| = 5 

Xác suất của biến cố B là:

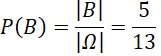
Biến cố C: "Cảng biển được chọn thuộc châu Phi"

Các cảng biển thuộc châu Phi là:

- Durban (thuộc Nam Phi)

- Lagos (thuộc Nigeria)

- Container Kênh Suez (thuộc Ai Cập)

- Kenya Mombasa (thuộc Kenya)

Do đó, số phần tử của tập hợp con C là:

 |C| = 4 

Xác suất của biến cố C là:

Bài 32 (trang 37):

Chọn ngẫu nhiên một vé xổ số có bốn chữ số được lập từ các chữ số từ 0 đến 9. Tính xác suất của biến cố : "Lấy được vé xổ số không có chữ số 3 ".

Bài giải chi tiết:

Số các vé xổ số có bốn chữ số được lập từ các chữ số từ 0 đến 9 là . Số các vé xổ số không có chữ số 3 là . Do đó có kết quả thuận lợi cho biến cố . Vậy .
Bài 33 (trang 37):

Trên mặt phẳng cho hình chữ nhật sao cho . Gọi là tập hợp tất cả các điểm với là các số nguyên và nằm bên trong (không kể trên cạnh) của hình chữ nhật . Lấy ngẫu nhiên một điểm của tập hợp . Tính xác suất của biến cố : "Điểm của tập hợp được lấy ra có ".

Bài giải chi tiết:

Ta có . Dễ thấy tập có 6 phần tử. Trong tất cả các điểm của tập , các điểm mỗi điểm có hoành độ và tung độ thoả mãn . Do đó có 5 kết quả thuận lợi cho biến cố . Vậy .