TRẮC NGHIỆM

Câu 1: Gieo hai đồng tiền một lần. Kí hiệu S,N để chỉ đông tiền lật sấp, lật ngửa.

Mô tả không gian mẫu

• A. Ω ={SN,NS}
• B. Ω ={NN,SS}
• C. Ω ={S,N}

• D. Ω ={SN,NS,SS,NN}

Câu 2: Phát biểu nào sau đây sai?

• A. Có những phép thử mà tập hợp Ω gồm các kết quả có thể xảy ra của phép thử đó hoàn toàn xác định. 

• B. Các kết quả xảy ra có tính ngẫu nhiên, ta có thể đoán trước được. Những phép thử như thế gọi là phép thử ngẫu nhiên (gọi tắt là phép thử) và tập hợp Ω gọi là không gian mẫu của phép thử.

• C. Các kết quả có thể xảy ra của một phép thử có khả năng xuất hiện như nhau được gọi là đồng khả năng.
• D. Kết quả thuận lợi cho biến cố A là một kết quả có thể của phép thử làm cho biến cố A xảy ra.

Câu 3: Hãy sắp xếp các bước sau để tính xác suất của biến cố A:

a) Đếm số kết quả có thể xảy ra, tức là đếm số phần tử của không gian mẫu Q

b) Đếm số kết quả thuận lợi cho biến cố A

c) Kiểm tra tính đồng khả năng đối với các kết quả có thể xảy ra của phép thử

d) Lập tỉ số giữa số kết quả thuận lợi cho biến cố A và tổng số kết quả có thể xảy ra.

• A. a) – b) – c) – d)
• B. b) – a) – c) – d) 

• C. c) – a) – b) – d)

• D. c) – b) – a) – d)

Câu 4: Một hộp có hai bi trắng được đánh số từ 1 đến 2, 3 viên bi xanh được đánh số từ 3 đến 5 và 2 viên bi đỏ được đánh số từ 6 đến 7. Lấy ngẫu nhiên hai viên bi:

Mô tả không gian mẫu

• A. Ω ={(m,n)|1 ≤ m ≤ 7,1 ≤ n ≤ 7}

• B. Ω ={(m,n)|1 ≤ m ≤ 7,1 ≤ n ≤ 7,m ≠ n}

• C. Ω ={(m,n)|1 ≤ m ≤ 5,6 ≤ n ≤ 7}
• D. Ω ={(m,n)|1 ≤ m ≤ 3,4 ≤ n ≤ 7}

Câu 5: Một hộp có 20 viên bi với kích thước và khối lượng như nhau. Bạn Ngân viết lên các viên bi đó các số 1, 2, 3, ..., 20; hai viên bi khác nhau thì viết hai số khác nhau. Xét phép thử “Lấy ngẫu nhiên một viên bi trong hộp”. Viết không gian mẫu của phép thử đó.

• A. Ω = {1; 2; 3; …; 20}.

• B. Ω = {20}.
• C. Ω = {1}.
• D. Ω = {1; 1; 2; 2; 3; 3; …; 20; 20}.

Câu 6: Một hộp có 20 viên bi với kích thước và khối lượng như nhau. Bạn Ngân viết lên các viên bi đó các số 1, 2, 3, ..., 20; hai viên bi khác nhau thì viết hai số khác nhau. Xét phép thử “Lấy ngẫu nhiên một viên bị trong hộp”. Tính xác suất của biến cố: “Số xuất hiện trên viên bi được lấy ra chia cho 7 dư 1”.

• A.

• B.

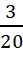
• C.
• D.

Câu 7: Viết ngẫu nhiên một số tự nhiên lớn hơn 499 và nhỏ hơn 1 000. Có tất cả bao nhiêu kết quả có thể xảy ra của phép thử trên?

• A. 499
• B. 501

• C. 500

• D. 498

Câu 8: Viết ngẫu nhiên một số tự nhiên lớn hơn 499 và nhỏ hơn 1 000. Tính xác suất của mỗi biến cố sau: A: “Số tự nhiên được viết ra chia hết cho 100”.

• A.

• B.
• C.
• D.

Câu 9: Gieo hai đồng tiền một lần. Kí hiệu S,N để chỉ đông tiền lật sấp, lật ngửa.

Xác định biến cố M: "hai đông tiền xuất hiện hai mặt không giống nhau"

• A. M = {NN, SS}

• B. M = {NS, SN}

• C. M = {NS, NN}
• D. M = {SS, SN}

Câu 10: Từ các chữ số 1,2,3,4 nhười ta lập các số tự nhiên có 3 chữ số khác nhau. Tính số phần tử không gian mẫu

• A. 16 

• B. 24 

• C. 6 
• D. 4

Câu 11: Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau: “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn 27”.

• A.

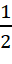
• B.
• C.
• D.

Câu 12: Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau: “Số xuất hiện trên thẻ được rút ra là số lớn hơn 19 và nhỏ hơn 51”.

• A.
• B.

• C.

• D.

Câu 13: Nhóm học sinh tình nguyện khối 9 của một trường trung học cơ sở có 6 bạn, trong đó có 3 bạn nam là: Trung (lớp 9A); Quý (lớp 9A); Việt (lớp 9C) và 3 bạn nữ là: An (lớp 9A); Châu (lớp 9B); Hương (lớp 9D). Chọn ngẫu nhiên một bạn trong nhóm đó để tham gia hoạt động tình nguyện của trường. Có tất cả bao nhiêu kết quả có thể xảy ra?

• A. 6

• B. 12
• C. 3
• D. 4

Câu 14: Có hai hộp thẻ. Hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 5, hộp thứ hai chứa các thẻ được đánh số từ 6 đến 9. Lấy ngẫu nhiên ở mỗi hợp 1 thẻ

Xác định biến cố M:"tổng các số ở hai thẻ lấy ra là số nguyên tố"

• A. M = {16, 38, 49, 56}

• B. M = {16, 29, 38, 47, 49, 56, 58}

• C. M = {61, 74, 92, 94, 65}
• D. M = {16, 38, 56}

Câu 15: Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan

Tính số phần tử của không gian mẫu

• A. 6  

• B. 24  

• C. 1  
• D. 4

Câu 16: Trên mặt phẳng cho năm điểm phân biệt A, B, C, D, E, trong đó không có ba điểm nào thẳng hàng. Hai điểm A, B được tô màu đỏ, ba điểm C, D, E được tô màu xanh. Bạn Châu chọn ra ngẫu nhiên một điểm tô màu đỏ và một điểm tô màu xanh (trong năm điểm đó) để nối thành một đoạn thẳng. Tính xác suất của mỗi biến cố sau: “Trong hai điểm được chọn ra, có điểm A”

• A.

• B.
• C.
• D.

Câu 17: Trên mặt phẳng cho năm điểm phân biệt A, B, C, D, E, trong đó không có ba điểm nào thẳng hàng. Hai điểm A, B được tô màu đỏ, ba điểm C, D, E được tô màu xanh. Bạn Châu chọn ra ngẫu nhiên một điểm tô màu đỏ và một điểm tô màu xanh (trong năm điểm đó) để nối thành một đoạn thẳng. Tính xác suất của mỗi biến cố sau: “Trong hai điểm được chọn ra, không có điểm C”.

• A.

• B.

• C.
• D.

Câu 18: Một bó hoa gồm 3 bông hoa màu đỏ và 1 bông hoa màu vàng. Bạn Linh chọn ngẫu nhiên 2 bông hoa từ bó hoa đó. Tính xác suất của mỗi biến cố sau:

R: “Trong 2 bông hoa được chọn ra, có đúng 1 bông hoa màu đỏ”

• A.

• B.
• C.
• D.

Câu 19: Một bó hoa gồm 3 bông hoa màu đỏ và 1 bông hoa màu vàng. Bạn Linh chọn ngẫu nhiên 2 bông hoa từ bó hoa đó. Tính xác suất của mỗi biến cố sau:

R: “Trong 2 bông hoa được chọn ra, có ít nhất 1 bông hoa màu đỏ”

• A.
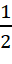
• B.
• C.

• D. 1

Câu 20: Chọn ngẫu nhiên một vé xổ số có bốn chữ số được lập từ các chữ số từ 0 đến 9. Tính xác suất của biến cố N: “Lấy được vé xổ số không có chữ số 3".

• A. 0,5616

• B. 0,6561

• C. 0,9
• D. 0,1