Giải VBT Toán 9 Cánh diều bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn
Giải chi tiết VBT Toán 9 cánh diều bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn. Tech12h sẽ hướng dẫn giải tất cả câu hỏi và bài tập với cách giải nhanh và dễ hiểu nhất. Hi vọng, thông qua đó học sinh được củng cố kiến thức và nắm bài học tốt hơn.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 1: ĐA GIÁC ĐỀU. HÌNH ĐA GIÁC ĐỀU TRONG THỰC TIỄN
Bài 1 (trang 106):
Quan sát Hình 6 và kể tên các đa giác có trong hình đó.
Hình 6
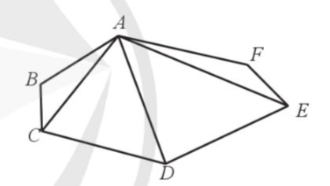
Bài giải chi tiết:
Các đa giác có trong Hình 6 là: tam giác ![]() , tam giác
, tam giác ![]() , tam giác
, tam giác ![]() , tam giác
, tam giác ![]() ; tứ giác
; tứ giác ![]() , tứ giác
, tứ giác ![]() , tứ giác
, tứ giác ![]() ; ngũ giác
; ngũ giác ![]() , ngũ giác
, ngũ giác ![]() ; lục giác
; lục giác ![]() .
.
Bài 2 (trang 106):
Cho tam giác ABC và D là một điểm nằm trong tam giác. Kẻ DE song song với AB (E thuộc cạnh AC ). Kẻ DF song song với BC ( F thuộc cạnh AC ).
a) Trong nhóm các điểm B, D, F, C và nhóm các điểm A, B, C, D, nhóm các điểm nào là 4 đỉnh của một tứ giác lồi? Vì sao?
b) Các điểm A, B, C, D, E có phải là các đỉnh của một ngũ giác lồi không? Vì sao?
Bài giải chi tiết:
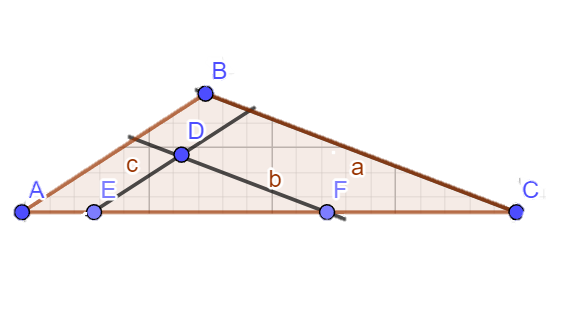
a)
Xét nhóm điểm B, D, F, C:
- Điểm D nằm trong tam giác ABC.
- DF song song với BC (F thuộc AC).
- B, D, F, C nằm trong tứ giác có các cạnh không cắt nhau trong và ngoài tứ giác
Từ đó, B, D, F, C tạo thành một tứ giác lồi vì tất cả các góc của nó đều nhỏ hơn 180 độ và không có điểm nào nằm bên trong của các cạnh nối hai điểm khác.
Xét nhóm điểm A, B, C, D:
- Điểm D nằm trong tam giác ABC.
- A, B, C là ba điểm nằm trên các đỉnh của tam giác ban đầu.
Nhóm các điểm A, B, C, D cũng tạo thành một tứ giác lồi vì tương tự như trên, tất cả các góc của tứ giác này đều nhỏ hơn 180 độ.
b) Ta có:
- DE song song với AB (E thuộc cạnh AC).
- Do DE song song với AB và D nằm trong tam giác ABC, nên E phải nằm trên đoạn AC giữa A và C.
Vì vậy, các điểm A, B, C, D, E tạo thành một ngũ giác lồi.
Bài 3 (trang 106):
Hãy vẽ một số đa giác (lồi) mà các đỉnh là một số điểm trong các điểm đã cho ở Hình 7
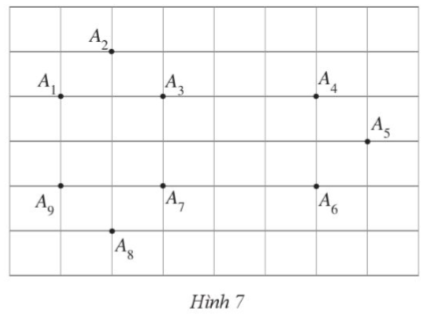
Bài giải chi tiết:
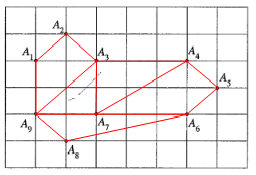
Bài 4 (trang 107):
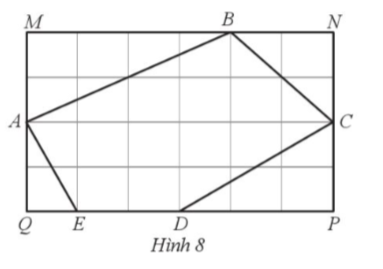
Cho hình chữ nhật ![]() và ngũ giác
và ngũ giác ![]() trên lưới ô vuông như Hình 8 , với cạnh của mỗi ô vuông nhỏ là
trên lưới ô vuông như Hình 8 , với cạnh của mỗi ô vuông nhỏ là ![]() . Tính tỉ số diện tích ngũ giác
. Tính tỉ số diện tích ngũ giác ![]() và diện tích hình chữ nhật
và diện tích hình chữ nhật ![]() (làm tròn đến hàng phần mười).
(làm tròn đến hàng phần mười).
Bài giải chi tiết:
Tổng diện tích các tam giác ![]() là:
là:
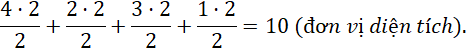
Diện tích hình chữ nhật ![]() là:
là: ![]() (đơn vị diện tích).
(đơn vị diện tích).
Diện tích ngũ giác ![]() là:
là: ![]() (đơn vị diện tích).
(đơn vị diện tích).
Tỉ số diện tích ngũ giác ![]() và diện tích hình chữ nhật
và diện tích hình chữ nhật ![]() là:
là: ![]() .
.
Bài 5 (trang 107):
Cho ngũ giác ![]() . Chứng minh:
. Chứng minh:
![]()
Bài giải chi tiết:
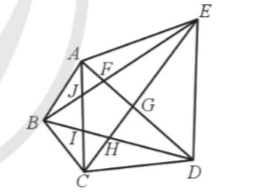
Áp dụng các bất đẳng thức tam giác ta có:![]() ;
; ![]() .
.
Do đó, ta có:
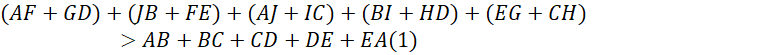
Mặt khác: 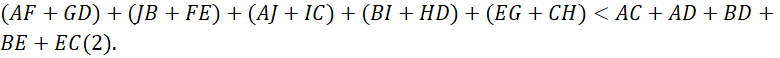
Từ (1) và (2) suy ra: ![]() .
.
Bài 6 (trang 107):
Cho ngũ giác đều ![]() và một điểm
và một điểm ![]() nằm trong ngũ giác. Gọi
nằm trong ngũ giác. Gọi ![]() ,
, ![]() lần lượt là các điểm nằm trên các đoạn thẳng
lần lượt là các điểm nằm trên các đoạn thẳng ![]() sao cho
sao cho ![]() . Chứng minh ngũ giác
. Chứng minh ngũ giác ![]() là ngũ giác đều.
là ngũ giác đều.
Bài giải chi tiết:
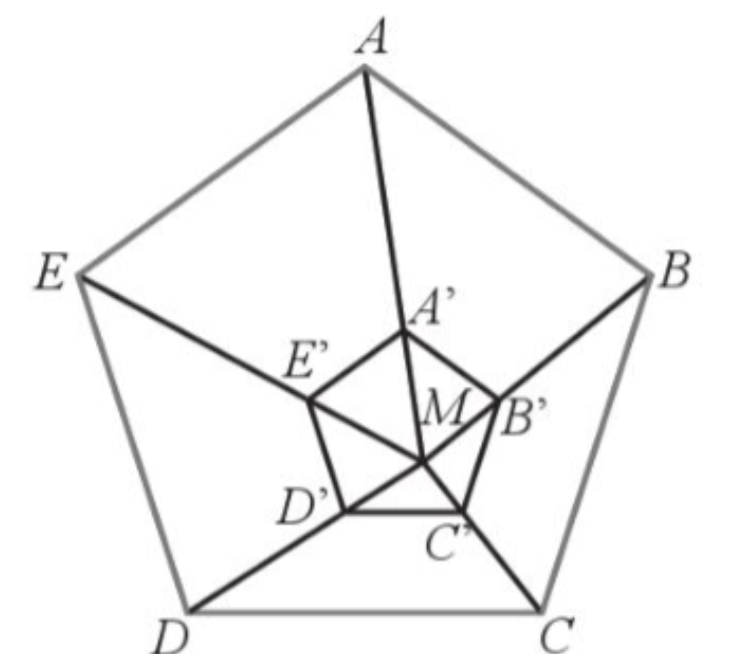
Từ giả thiết suy ra:
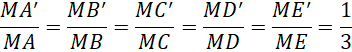
Do đó ![]() . Kẻ
. Kẻ ![]() vuông góc với
vuông góc với ![]() (
( ![]() thuộc
thuộc ![]() . Tam giác vuông
. Tam giác vuông ![]() có
có ![]() và
và ![]() nên
nên ![]() do đó
do đó ![]() .
.
Nếu ![]() là lục giác đều thì
là lục giác đều thì ![]() , do đó
, do đó ![]() hay
hay ![]() . Ngược lại, nếu
. Ngược lại, nếu ![]() thì
thì ![]() và các cạnh của lục giác
và các cạnh của lục giác ![]() bằng nhau (1).
bằng nhau (1).
Mặt khác, các góc của lục giác ![]() đều bằng
đều bằng ![]() nên lục giác
nên lục giác ![]() là lục giác đều. Vậy hệ thức liên hệ giữa
là lục giác đều. Vậy hệ thức liên hệ giữa ![]() và
và ![]() để lục giác
để lục giác ![]() là lục giác đều là
là lục giác đều là ![]() .
.
Bài 7 (trang 107):
Cho ngũ giác đều ![]() , đoạn
, đoạn ![]() cắt các đoạn
cắt các đoạn ![]() và
và ![]() lần lượt tại
lần lượt tại ![]() và
và ![]() . Chứng minh rằng:
. Chứng minh rằng:
a) Các tam giác ![]() và
và ![]() là các tam giác cân;
là các tam giác cân;
b) ![]() là phân giác của góc
là phân giác của góc ![]() ;
;
c) ![]() .
.
Bài giải chi tiết:
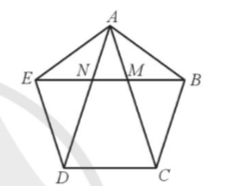
a) Ngũ giác ![]() là ngũ giác đều nên tam giác
là ngũ giác đều nên tam giác ![]() cân tại
cân tại ![]() và
và ![]() , tam giác
, tam giác ![]() cân tại
cân tại ![]() và
và ![]() . Suy ra
. Suy ra ![]() nên tam giác
nên tam giác ![]() cân tại
cân tại ![]() . Tương tự tam giác
. Tương tự tam giác ![]() cân tại
cân tại ![]() và
và ![]() . Mặt khác:
. Mặt khác:
![]() ;
; ![]() .
.
Suy ra tam giác ![]() cân tại
cân tại ![]() .
.
b) Do ![]() và
và ![]() nên
nên ![]() . Từ đó suy ra
. Từ đó suy ra ![]() . Vì vậy
. Vì vậy ![]() là phân giác của góc
là phân giác của góc ![]() .
.
c) Dễ thấy ![]() do có chung cạnh AB và điểm M thuộc AC suy ra
do có chung cạnh AB và điểm M thuộc AC suy ra ![]() hay
hay ![]() .
.
Bài 8 (trang 107):
Ở Hình 9 biết ![]() là lục giác đều, chứng minh rằng lục giác
là lục giác đều, chứng minh rằng lục giác ![]() cũng là lục giác đều.
cũng là lục giác đều.
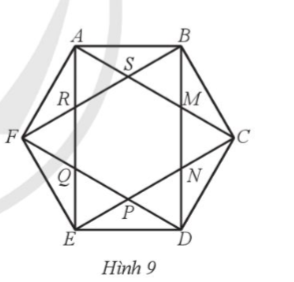
Bài giải chi tiết:
Lục giác ABCDEF là lục giác đều nên AB = BC = CD = DE = EF = FA và ![]()
Ta cũng có tổng 6 góc của lục giác đều ABCDEF bằng tổng các góc của hai tứ giác ABCD và AFED, tức là bằng 2.360° = 720°.
Do đó: ![]()
Xét ∆AFB cân tại A (do AB = AF) ta có:
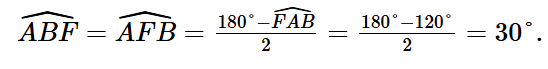
Hay: ![]()
Tương tự, đối với ∆ABC cân tại B ta có: ![]() hay
hay ![]()
Do đó ta có: ![]() Nên ∆ABS cân tại S.
Nên ∆ABS cân tại S.
Suy ra 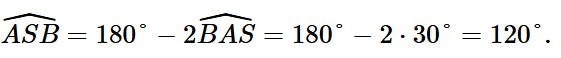
Bài 9 (trang 107):
Người ta chia đường tròn ![]() thành 6 cung bằng nhau như sau:
thành 6 cung bằng nhau như sau:
- Trên đường tròn
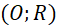 , lấy điểm
, lấy điểm 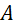 tuỳ ý;
tuỳ ý; - Vẽ một phần đường tròn
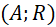 cắt
cắt 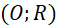 tại
tại 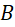 và
và 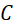 ;
; - Vẽ một phần đường tròn
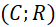 cắt
cắt 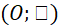 tại
tại 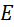 (khác
(khác 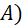 ;
; - Vẽ một phần đường tròn
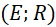 cắt
cắt 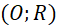 tại
tại 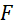 (khác
(khác 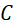 );
); - Vẽ một phần đường tròn
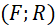 cắt
cắt 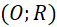 tại
tại 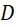 (khác
(khác 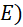 .
.
Nối ![]() với
với ![]() với
với ![]() với
với ![]() với
với ![]() với
với ![]() với
với ![]() , ta được lục giác
, ta được lục giác ![]() . Chứng minh:
. Chứng minh:
a) Lục giác ![]() là lục giác đều;
là lục giác đều;
b) ![]() là các đường kính của đường tròn
là các đường kính của đường tròn ![]() ;
;
c) Các tứ giác ![]() đều là hình thang cân.
đều là hình thang cân.
Bài giải chi tiết:
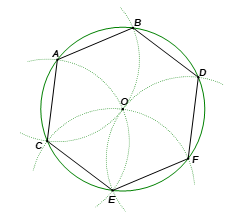
a) Nối OA, OB, OC, OD, OE, OF.
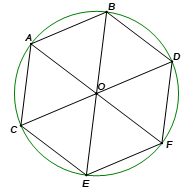
Từ giả thiết ta có sáu cung AB, AC, CE, EF, FD, DB bằng nhau nên ![]()
Xét ∆AOB và ∆BOD có:
OA = OB; ![]() ; OB = OD.
; OB = OD.
Do đó ∆AOB = ∆BOD (c.g.c), suy ra AB = BD (hai cạnh tương ứng).
Mặt khác, ta có AB = AC = CE = EF = FD = R.
Nên AB = AC = CE = EF = FD = DB. (1)
Ta có: ![]()
![]()
Suy ra ![]() , do đó
, do đó ![]()
Xét ∆AOB có OA = OB và nên ∆AOB là tam giác đều.
Do đó ![]()
Chứng minh tương tự, ta cũng có ∆OAC đều nên ![]()
Khi đó, ![]()
Tương tự, ta chứng minh được:
![]()
Từ (1) và (2) ta có ABDFEC là lục giác đều.
b) Do ABDFEC là lục giác đều nên ba đường chéo AF, BE, CD cắt nhau tại O.
Do đó AF, BE, CD là các đường kính của đường tròn (O; R).
c) Chứng minh tương tự ở câu a, ta chứng minh được ∆AOC, ∆OCE là các tam giác đều. Suy ra ![]()
Mà hai góc này ở vị trí so le trong nên AO // CE hay AF // CE.
Tứ giác ACEF có AF // CE nên là hình thang.
Lại có ![]() nên ACEF là hình thang cân.
nên ACEF là hình thang cân.
Chứng minh tương tự, ta cũng có các tứ giác ABDC, BECA đều là hình thang cân.
Bài 10 (trang 108):
Cho tam giác đều ![]() cạnh
cạnh ![]() . Vẽ về phía ngoài tam giác
. Vẽ về phía ngoài tam giác ![]() các hình chữ nhật
các hình chữ nhật ![]() và
và ![]() sao cho
sao cho ![]() . Tìm hệ thức liên hệ giữa
. Tìm hệ thức liên hệ giữa ![]() và
và ![]() để hình lục giác
để hình lục giác ![]() là lục giác đều.
là lục giác đều.
Bài giải chi tiết:
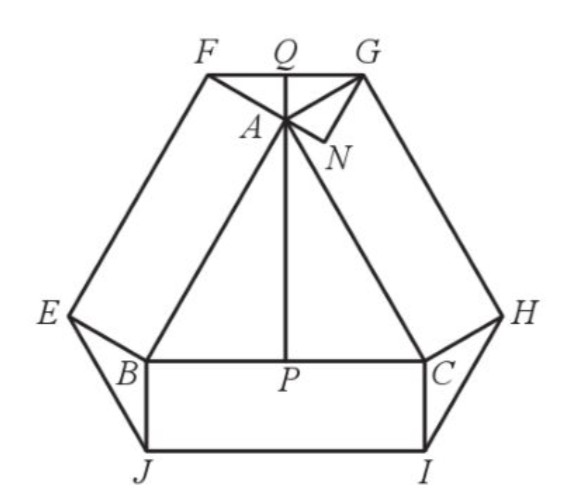
Gọi ![]() là trung điểm của
là trung điểm của ![]() và
và ![]() là giao điểm của các đường thẳng
là giao điểm của các đường thẳng ![]() và
và ![]() .
.
Ta có: ![]() ,
,
![]()
Do đó ![]() . Kẻ
. Kẻ ![]() vuông góc với
vuông góc với ![]() (
( ![]() thuộc
thuộc ![]() . Tam giác vuông
. Tam giác vuông ![]() có
có ![]() và
và ![]() nên
nên ![]() do đó
do đó ![]() .
.
Nếu ![]() là lục giác đều thì
là lục giác đều thì ![]() , do đó
, do đó ![]() hay
hay ![]() . Ngược lại, nếu
. Ngược lại, nếu ![]() thì
thì ![]() và các cạnh của lục giác
và các cạnh của lục giác ![]() bằng nhau (1). Mặt khác, các góc của lục giác
bằng nhau (1). Mặt khác, các góc của lục giác ![]() đều bằng
đều bằng ![]() nên lục giác
nên lục giác ![]() là lục giác đều. Vậy hệ thức liên hệ giữa
là lục giác đều. Vậy hệ thức liên hệ giữa ![]() và
và ![]() để lục giác
để lục giác ![]() là lục giác đều là
là lục giác đều là ![]() .
.
Bài 11 (trang 108): Tính số đo mỗi góc của một đa giác đều có ![]() cạnh trong mỗi trường hợp sau:
cạnh trong mỗi trường hợp sau:
a) ![]() ;
;
b) ![]()
c) ![]() .
.
Bài giải chi tiết:
Để tính số đo mỗi góc của một đa giác đều có ![]() cạnh, ta sử dụng công thức:
cạnh, ta sử dụng công thức:
Số đo mỗi góc ![]()
a) ![]()
Số đo mỗi góc ![]()
b) ![]()
Số đo mỗi góc ![]()
c) ![]()
Số đo mỗi góc ![]()
Bài 12 (trang 108):
Cho đa giác đều ![]() . Chứng minh các đường trung trực của các cạnh
. Chứng minh các đường trung trực của các cạnh ![]() cùng đi qua một điểm.
cùng đi qua một điểm.
Bài giải chi tiết:
Gọi ![]() là tâm của đa giác đều
là tâm của đa giác đều ![]() . Ta có
. Ta có ![]() suy ra
suy ra ![]() nằm trên đường trung trực của cạnh
nằm trên đường trung trực của cạnh ![]() . Tương tự ta có
. Tương tự ta có ![]() nằm trên các đường trung trực của các đoạn
nằm trên các đường trung trực của các đoạn ![]() . Từ đó suy ra điều phải chứng minh.
. Từ đó suy ra điều phải chứng minh.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải VBT Toán 9 cánh diều , Giải VBT Toán 9 CD, Giải VBT Toán 9 bài 1: Đa giác đều. Hình đa giác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận