CHƯƠNG IV - HỆ THỨC LƯỢNG GIÁC TRONG TAM GIÁC VUÔNG

BÀI 3 - ỨNG DỤNG TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN

18. Tính chiều cao của cột cờ (làm tròn kết quả đến hàng phần trăm của mét), biết bóng của cột cờ được chiếu bởi ánh sáng Mặt Trời xuống mặt đất dài 10,5 m và góc tạo bởi tia sáng với phương nằm ngang là 36°.

Bài giải chi tiết:

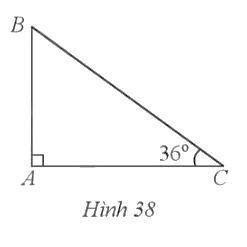
Tam giác vuông tại ở Hinh 38 mô tả cột cờ có bóng nắng của cột cờ trên mặt đất là và góc tạo bởi tia nắng với phương nằm ngang là . 

Vì tam giác vuông tại nên

19. Một khối u (ở vị trí A) của một bệnh nhân cách da mặt 5,7 cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia (ở vị trí B) cách hình chiếu của khối u (ở vị trí C) trên da mặt là 8,3 cm (Hình 19).

a) Hỏi góc tạo bởi chùm tia gamma với da mặt là bao nhiêu độ (làm tròn kết quả đến hàng phần mười)?

b) Chùm tia phải đi một đoạn dài bao nhiêu centimét để đến được khối u (làm tròn kết quả đến hàng phần mười)?

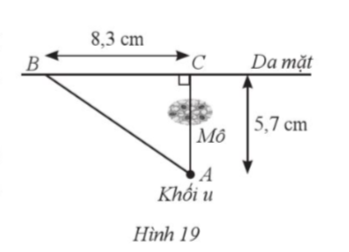
Bài giải chi tiết:

Theo đề bài, ta có: độ dài đường đi của chùm tia gamma tới khối u là ; góc tạo bởi chùm tia gamma với da mặt là góc . 

a) Vì tam giác vuông tại nên tan .

Suy ra . Vậy góc tạo bới chùm tia gamma với da mặt xấp xi .

b) Vi tam giác vuông tại nên

20. Một người đứng chào cờ (ở vị trí 4) cách cột cờ (ở vị trí C) với AC = 20 m. Người đó đặt mắt tại vị trí B cách mặt đất một khoảng là AB = 1, 5 m. Người đó nhìn lên đỉnh cột cờ (ở vị trí E) theo phương BE tạo với phương nằm ngang BD một góc là = 32 (Hình 20). Tính chiều cao của cột cờ (làm tròn kết quả đến hàng đơn vị của mét).

Bài giải chi tiết:

Ta chứng minh được là hình chữ nhật. Suy ra và .

Vì tam giác vuông tại nên .

Vậy chiều cao của cột cờ là: .

21. Bạn Hoà vẽ mặt cắt đứng phần mái của một ngôi nhà có dạng tam giác cân ABC (mái hai dốc). Biết rằng góc tạo bởi phần mái nhà và mặt phẳng nằm ngang là = 25  và độ dài mỗi bên dốc mái là 3,5 m (Hình 21). Tính độ dài đoạn thẳng BC (làm tròn kết quả đến hàng phần mười của mét).

Bài giải chi tiết:

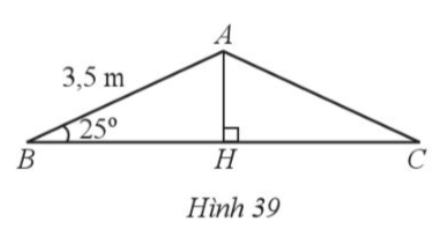
Kẻ đường cao của tam giác (Hình 39.

Vì tam giác vuông tại nên

Do (cạnh huyền - cạnh góc

22. Trên mặt biển, khi khoảng cách từ ca nô đến chân tháp hải đăng là AB = 300 m, một người đứng trên tháp hải đăng đó, đặt mắt tại vị trí C và nhìn về phía ca nô theo phương CA tạo với phương nằm ngang Cx một góc là = 27  (minh hoạ ở Hình 22). Tỉnh chiều cao BH của tháp hải đăng (làm tròn kết quả đến hàng phần trăm của mét), biết AB // Cx và độ cao từ tầm mắt của người đó đến đỉnh tháp hải đăng là CH = 2,1 m.

Bài giải chi tiết:

Do nên .

Vì tam giác vuông tại nên .

Chiều cao của tháp hải đăng là:

23. Một chiếc thuyền đi với tốc độ 20 km/h theo hướng Đông trong 1 giờ 30 phút từ vị trí P đến vị trí A. Sau đó, nó sẽ đi theo hướng Bắc với cùng tốc độ trong 3 giờ 30 phút đến vị trí B (Hình 23). Tính góc so với hướng Đông mà thuyền đi từ vị trí P đến vị trí B (làm tròn kết quả đến hàng đơn vị của phút).

Bài giải chi tiết:

Đổi: 1 giờ 30 phút giờ; 3 giờ 30 phút giờ.

Theo đề bài, ta có góc so với hướng Đông mà thuyền đi từ vị tri đến vị tri là góc .

Quãng đường là: .

Quãng đường là: .

Xét tam giác vuông tại , ta có: .

Suy ra .

Vậy góc so với hướng Đông mà thuyền đi từ vị tri đến vị tri xấp xi .

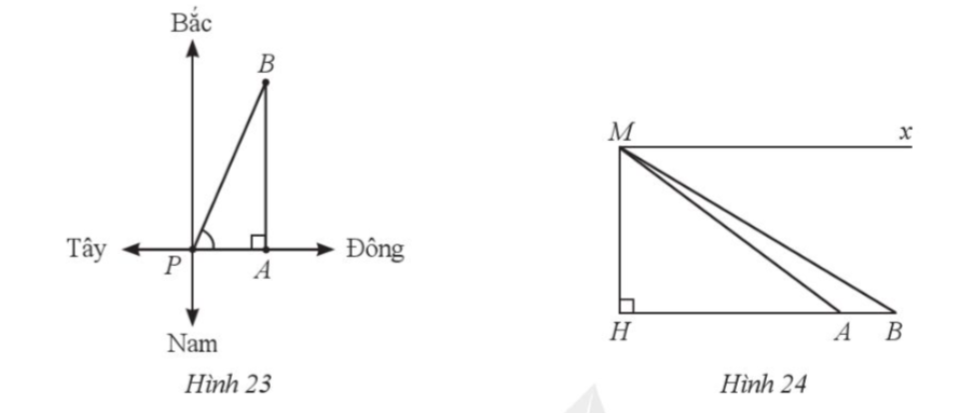
24. Từ một máy bay trực thăng, một người đặt mặt tại vị trí M ở độ cao MH = 920 m. Người đó nhìn hai vị trí A và B của hai đầu một cây cầu theo phương MA và MB tạo với phương nằm ngang Mx các góc lần lượt là AMx = 37° và BMx = 31° với Mx // AB (Hình 24). Hỏi độ dài AB của cây cầu là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Bài giải chi tiết:

Do nên .

Vi tam giác vuông tại nên .

Vì tam giác vuông tại nên .

Mà , suy ra .

Vậy độ dài của cây cầu khoảng 310 m .

25. Từ một đài quan sát, một người đặt mắt tại vị trí B. Người đó nhìn thấy một chiếc ô tô ở vị trí C theo phương BC tạo với phương nằm ngang Bx một góc là CBx = 23° với Bx // AC. Khi đó, khoảng cách giữa ô tô và chân đài quan sát là AC = 1284 m. Nếu ô tô từ vị trí C tiếp tục đi về phía chân đài quan sát với tốc độ 60 km/h thì sau 1 phút, người đó nhìn thấy ô tô ở vị trí D với góc = (Hình 25). 

a) Tính chiều cao của đài quan sát (làm tròn kết quả đến hàng đơn vị của mét), biết độ cao từ tầm mắt của người đó đến đình đài quan sát là 3 m.

b) Tính số đo góc (làm tròn kết quả đến hàng đơn vị của phút).

c) Tỉnh khoảng cách từ mắt người quan sát đến vị trí D (làm tròn kết quả đến hàng đơn vị của mét).

Bài giải chi tiết:

a) Do nên .

Vì tam giác vuông tại nên .

Vâyy chiều cao của đài quan sát khoảng: .
b) Đổi: phút.

Do nên ta tính được .

Quãng đường là: .

Suy ra (m).

Xét tam giác vuông tại , ta có: .

Suy ra .

Mà , suy ra .

c) Vì tam giác vuông tại nên . Suy ra

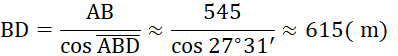
26. Flycam là từ viết tắt của Fly camera. Đây là thiết bị bay không người lái có lắp camera hay máy ảnh để quay phim hoặc chụp ảnh từ trên cao. Một chiếc Flycam đang ở vị trí A cách cây cầu BC (theo phương thẳng đứng) một khoảng AH = 120 m. Biết góc tạo bởi phương AB, AC với các phương vuông góc với mặt cầu tại B, C lần lượt là = 30  , = 27  Hình 26). Tính độ dài BC của cây cầu (làm tròn kết quả đến hàng phần trăm của mét).

Bài giải chi tiết:

Ta chúng minh được . Suy ra

Vì tam giác vuông tại nên

Vì tam giác vuông tại nên

Vậy độ dài của cây cầu là: .