TRẮC NGHIỆM

Câu 1: Một khúc sông rộng khoảng 250 m. Một chiếc thuyền muốn qua sông theo phương ngang nhưng bị dòng nước đẩy theo phương xiên, nên phải đi khoảng 320 m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy thuyền lệch đi một góc bao nhiêu độ?

(Hình ảnh minh họa)

• A.
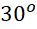
• B.
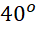
• C.

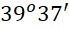
• D.

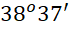
Câu 2: Một cột đèn điện AB cao 6 m có bóng in trên mặt đất là AC 3,5 m. Hãy tính góc BCA (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất.

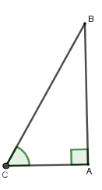
• A.

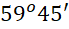
• B.
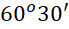
• C.
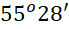
• D.

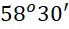
Câu 3: Một máy bay đang bay ở độ cao 10 km so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? (  làm tròn kết quả đến hai chữ số phần thập phân).

(Hình ảnh minh họa)

• A. 40,02 km
• B. 44,55 km

• C. 37,32 km

• D. 38,75 km

Câu 4: Nhà bạn Minh có một chiếc thang dài 4 m. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)

• A. 1,71 m

• B. 1,69 m

• C. 1,66 m
• D. 1,75 m

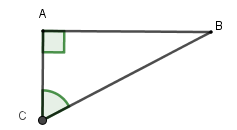
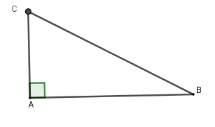
Câu 5: Người ta muốn đo vị trí BC bị ngăn cách bởi một cái ao sâu. Vì thế nên người ta đã chọn thêm một điểm A, sao cho ba điểm A, B, C tạo thành tam giác vuông tại C.

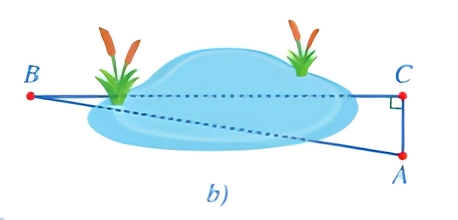
Công thức tính khoảng cách của vị trí B, C là:

• A.
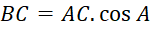
• B.

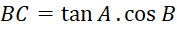
• C.

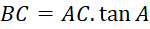
• D.

Cho bài toán: Trong một buổi ôn tập kiến thức toán, giáo viên vẽ một hình tam giác lên bảng. Biết tam giác có góc vuông, cạnh huyền bằng (cm) và góc bằng . Giáo viên yêu cầu học sinh nêu công thức tính cạnh và theo và

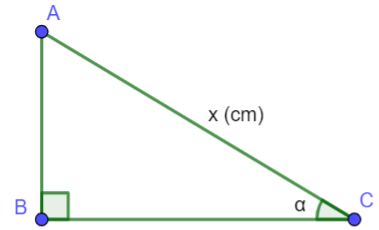
Hãy trả lời câu hỏi của Câu 6 và Câu 7

Câu 6: Công thức tính cạnh theo và là:

• A. (cm)
• B. (cm)
• C. (cm)

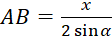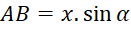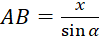• D. (cm)

Câu 7: Công thức tính cạnh theo và là:

• A.

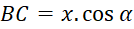
• B.
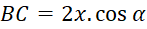
• C.
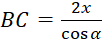
• D.

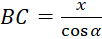
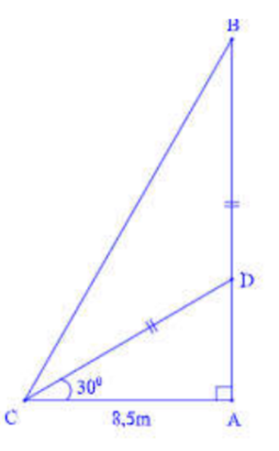
Câu 8: Giông bão thổi mạnh, một cây tre gãy gập xuống làm ngọn cây chạm đất và ngọn cây tạo với mặt đất một góc . Người ta đo được khoảng cách từ chỗ ngọn cây chạm đất đến gốc tre là . Giả sử cây tre mọc vuông góc với mặt đất, hãy tính chiều cao của cây tre đó (làm tròn đến chữ số thập phân thứ hai)

• A. 12,72 m
• B. 13,72 m
• C. 15,72 m

• D. 14,72 m

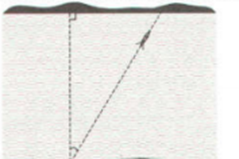
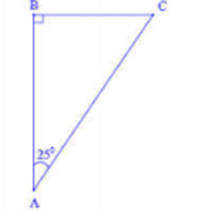
Câu 9: Một con thuyền qua khúc sông với vận tốc mất hết 6 phút. Do dòng nước chảy mạnh nên đã đẩy con thuyền đi qua con sông trên đường đi tạo với bờ một góc . Hãy tính chiều rộng của con sông?

• A. 150,5 m
• B. 139,2 m

• C. 147,92 m

• D. 105,92 m

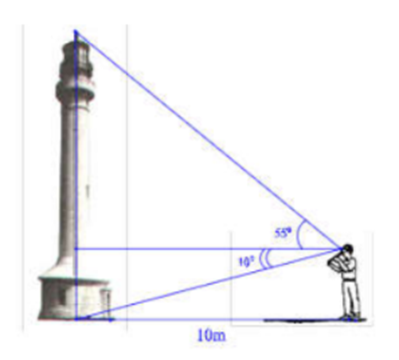
Câu 10: Một ngurời quan sát đứng cách một cái tháp , nhìn thẳng đỉnh tháp và chân tháp lần lượt dưới một góc và so với phương ngang của mặt đất. Hãy tính chiều cao của tháp.

• A. 16 m

• B. 18 m
• C. 17 m
• D. 15 m

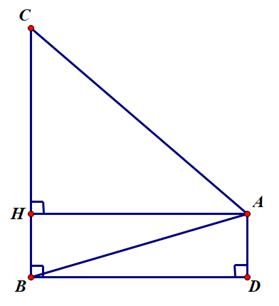
Câu 11: Hai chiếc thuyền A và B ở vị trí được minh họa như hình dưới dây. Tính khoảng cách giữa chúng. (làm tròn đến mét)

• A. 352 m

• B. 362 m

• C. 342 m
• D. 332 m