CHƯƠNG V - ĐƯỜNG TRÒN

BÀI 4 - GÓC Ở TÂM, GÓC NỘI TIẾP

27. Trong các góc ABC, DEG, HIK, MNP, QRS, XYZ lần lượt ở các hình 32a, 32b, 32c, 32d, 32e, 32g, góc nào là góc nội tiếp? Vì sao?

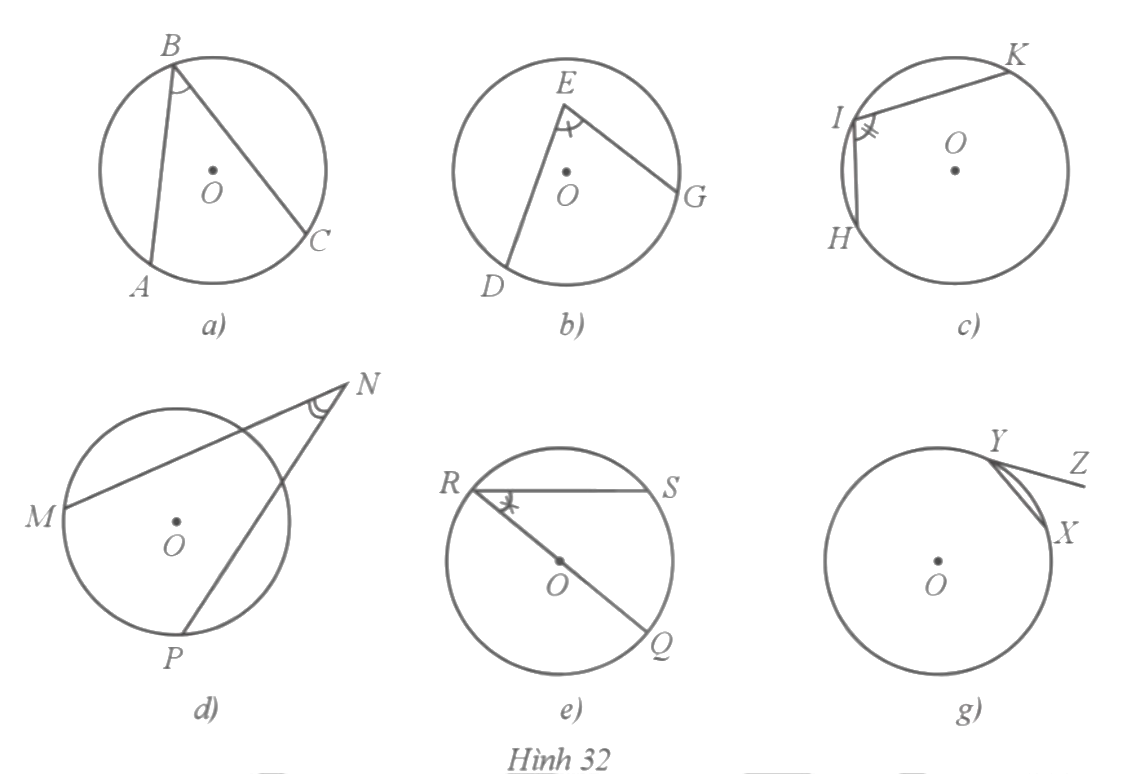
Bài giải chi tiết:

Do góc nội tiếp là góc có đỉnh thuộc đường tròn và hai cạnh chứa hai dây cung của đường tròn đó nên các góc là góc nội tiếp.

28. Nhận định nào sau đây là sai?

A. Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.

B. Góc nội tiếp là góc có đỉnh thuộc đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

C. Góc nội tiếp chắn nửa đường tròn có số đo bằng 90°.

D. Số đo của cung AB được kí hiệu là sđAB.

Bài giải chi tiết:

D

29. Biểu đồ hình quạt tròn ở Hình 33 biểu diễn số lớp học cấp trung học cơ sở của năm tỉnh Tây Nguyên tỉnh đến ngày 30/9/2021 (tính theo tỉ số phần trăm). Hãy cho biết các cung tương ứng với phần biểu diễn số lớp học cấp trung học cơ sở của các tỉnh Kon Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng tỉnh đến ngày 30/9/2021 lần lượt có số đo là bao nhiêu độ?

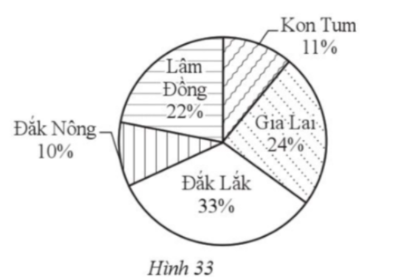
Bài giải chi tiết:

Các cung tương ứng với phần biểu diễn số lớp học cấp trung học cơ sở của các tỉnh Kon Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng tính đến ngày 30/9/2021 lần lượt có số đo là: .

30. Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A và = 50°. So sánh các cung nhỏ AB, BC.

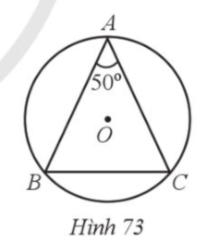
Bài giải chi tiết:

(Hình 73 ) 

Do tam giác cân tại nên

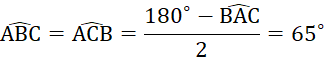
Ta có: số đo cung nhỏ bằng , số đo cung nhỏ bằng . Vậy cung nhò lớn hơn cung nhỏ .

31. Bạn An đố bạn Bình: “Hãy xác định tâm của đường tròn mà chỉ dùng ê ke." Bạn Bình đã xác định tâm O của đường tròn như sau:

- Lần thứ nhất: đặt góc vuông của ê ke tại điểm A, hai cạnh góc vuông của ê ke lần lượt cắt đường tròn tại hai điểm (gọi hai điểm đó là B, C);

- Lần thứ hai: đặt góc vuông của ê ke tại điểm H, hai cạnh góc vuông của ê ke lần lượt cắt đường tròn tại hai điểm (gọi hai điểm đó là 1, K).

Quan sát Hình 34 và chứng minh răng bằng cách làm hai lần như trên thì bạn Bình đã giải được câu đố của bạn An.

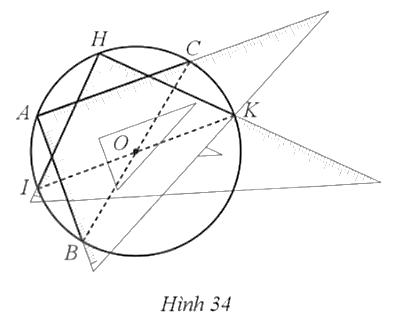
Bài giải chi tiết:

Ta có: nên và là các góc nội tiếp chắn nửa đường tròn. Suy ra và là hai đường kính của đường tròn . Khi đó, cắt tại tâm của đường tròn.

32. Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn. Vẽ hai tiếp tuyến tại A và B của đường tròn (0), hai tiếp tuyến đó cắt nhau tại M.

a) Tính số đo cung nhỏ AB và số đo cung lớn AB nếu = 40°.

b) Tính diện tích của tứ giác OAMB theo R nếu số đo cung nhỏ AB bằng 120°.

Bài giải chi tiết:

a) Do nên . Suy ra số đo cung nhỏ bằng và số đo cung lớn bằng .
b) Do số đo cung nhỏ bằng suy ra . Do đó .

Do tam giác vuông tại nên .

Vì (c.c.c) nên diện tích tứ giác là:

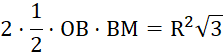
33. Cho hai đường tròn (O; R) và (O; R) cắt nhau tại hai điểm A, B. Kẻ đường kính AC của đường tròn (O) và đường kinh AD của đường tròn (O). So sánh độ dài dây BC của đường tròn (O) và độ dài dây BD của đường tròn .

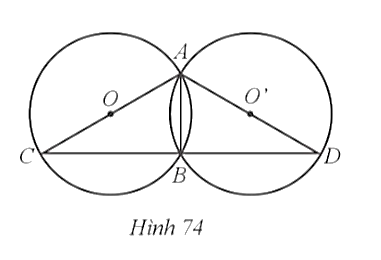
Bài giải chi tiết:

Ta có: lần lượt là đường kính của đường tròn nên . Do đó (cạnh huyền - cạnh góc vuông). Suy ra .

Vậy độ dài dây của đường tròn bằng độdây của đường tròn .

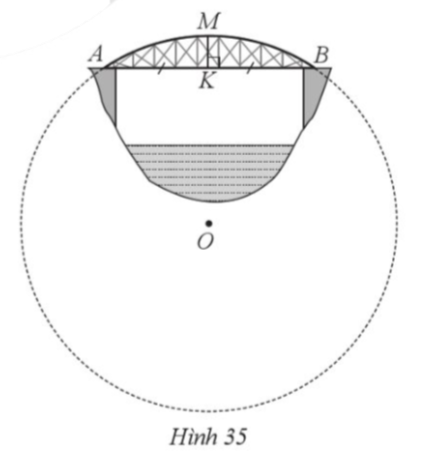
34. Một chiếc cầu được thiết kế như mộtcung AB của đường tròn (O) với độ dài AB = 40 m và chiều cao MK = 6 m (Hình 35). Tính bán kính của đường tròn chứa cung AMB (làm tròn kết quả đến hàng phần mười của mét). 

Bài giải chi tiết:

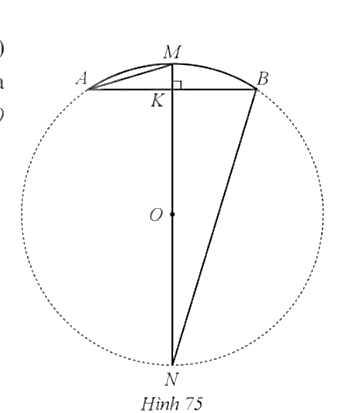
Kẻ đường kính của đường tròn (Hinh 75). Khi đó, là đường trung trực của đoạn thẳng và cắt tại . Suy ra điểm thuộc và .

Do nên

hay .

Gọi là bán kính của đường tròn . 

Ta có: .

Vậy bán kính của đường tròn chứa cung là .

35. Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm O đường kính AC. Trên tia BH, lấy điểm D sao cho H là trung điểm của đoạn thẳng BD. Nối A với D cắt đường tròn (O) tại E. Chứng minh:

a) CH là tia phân giác của góc ;

b) OH // EC.

Bài giải chi tiết:

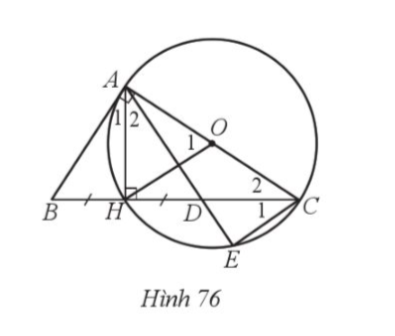
a) Do (c.c.c). Suy ra .

Mà (vì cùng phụ )

và (hai góc nội tiếp cùng chắn cung ), suy ra .

Vâyy là tia phân giác của góc .
b) (góc ờ tâm và góc nội tiếp cùng chắn cung ) và

(vì là tia phân giác của góc ) nên .

Vậy (hai góc đồng vị bằng nhau).

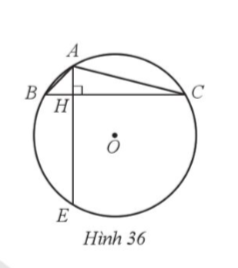
36. Cho đường tròn (0; 1 dm) và ba điểm A, B, C nằm trên đường tròn sao cho = 45°, = 15°. Kẻ AH vuông góc với BC tại H, tia AH cắt đường tròn (0) tại E (Hình 36). Tính:

a) Số đo cung nhỏ CE và số đo cung lớn BC;

b) Độ dài các đoạn thẳng AC, BC. 

Bài giải chi tiết:

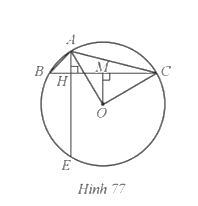
Kẻ vuông góc với tại (Hìh 77).

a) Ta có: nên .

Do đó số đo cung nhỏ bằng .

Ta lại có: nên

Do đó số đo cung lớn bằng .

b) Ta có: .

Suy ra tam giác vuông cân tại .

Do đó .

Do (cạnh huyền - cạnh góc vuông) nên .

Ta có: .

Do tam giác vuông tại nên .

Vậy