LUYỆN TẬP CHUNG

Bài tập 9.31: Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.

Giải nhanh:

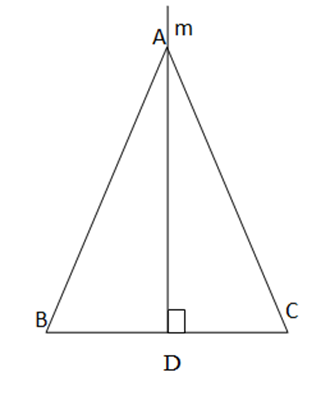
Từ A kẻ đường thẳng m vuông góc với BC tại trung điểm D của BC

=> AD là đường trung tuyến của BC

Ta có  ∆ ADB và  ∆ ADC đều vuông tại D

Xét  ∆ ADB và  ∆ ADC , ta có:    AD chung;  DB = DC; vuông tại D

=>  ∆ ADB =  ∆ ADC => AB= AC => ∆ABC cân tại A

Bài tập 9.32: Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳngCM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chúng minh đường thẳng BM, vuông góc với đường thẳng CN

Giải nhanh:

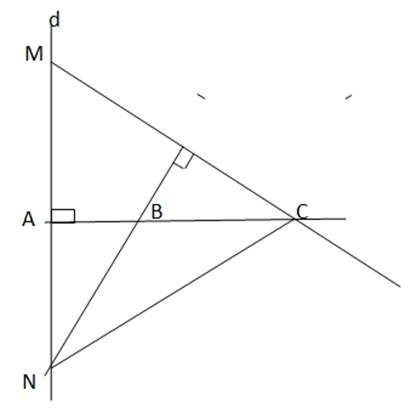
Ta có: BN ⊥ CM, CA ⊥ MN. CA và BN cắt nhau tại B

=> B là trực tâm của ∆ MNC  => MB ⊥ CN

Bài tập 9.33: Có một mảnh tôn hình tròn cần đục lỗ ở tâm. Làm thế nào để xác đinh được tâm của mảnh tôn đó?

Giải nhanh:

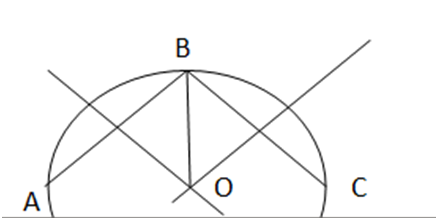
- Lấy ba điểm phân biệt A, B, C trên đường viền ngoài mảnh tôn.

- Vẽ đường trung trực AB và BC. Hai đường cắt nhau tại D là tâm cần xác định.

Bài tập 9.34: Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.

Giải nhanh:

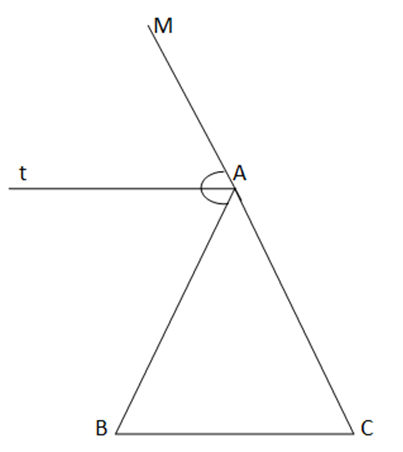
Gọi AM là tia đối của AC. At là đường phân giác của => =

Ta có At // BC => = ( 2 góc so le); = ( 2 góc đồng vị)

mà = ; ==> Tam giác ABC cân tại A

Bài tập 9.35: Kí hiệu S(ABC) là diện tích tam giác ABC. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC

a) Chúng minh S(GBC) = 1/3 S(ABC)

Gợi ý: sử dụng GM= 1/3 AM để chứng minh  S(GMB) = 1/3 S(ABM) ,  S(GCM) = 1/3 S(ACM)

b)Chứng minh S(GCA) = S(GAB) = 1/3 S(ABC)

Giải nhanh:

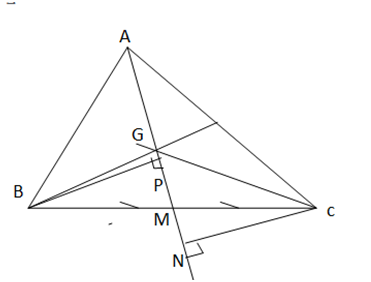
a) Vì G là trọng tâm tam giác ABC nên GM= AM

Kẻ BP ⊥ AM ta có S_GMB= BP . GM.   S_ABM =  BP . AM.

Ta có S_GMB =   BP . GM.=>  S_GMB=   BP .   AM=>  S_GMB =   AM.   BP

=> S_GMB=    S_ABM (1)

Tương tự, kẻ CN ⊥ AM, ta có  S_GMC = CN . GM   S_ACM =  CN . AM.

mà  GM= AM  => S_GMC=  S_ACM (2)

Cộng (1) và (2) ta có: S_GMB + S_GMC=  S_AMC + S_ABM=> S_GBC = S_ABC

b) BP ⊥ AM => BP ⊥ AG

 CN ⊥ AM =>  CN ⊥ AG

Ta có S_GAB= BP . AG;  S_GAC=  CN . AG.

Xét ∆BPM vuông tại P và ∆CNM vuông tại N có: BM= CM; =  

=> ∆ BPM =  ∆ CNM => BP = CN => S_GAB = S_GAC

Có AG=  AM

S_ACB =  S_GAB +  S_GAC+ S_GCB => S_ACB =  S_GAB +  S_GAC + S_ABC 

=> S_ABC = 2 S_GAC => S_ABC = S_GAC = S_GAB