BÀI TẬP CUỐI CHƯƠNG VII

Bài tập 7.42: Một hãng taxi quy định giá cước như sau: 0,5 km đầu tiên giá 8 000 đồng; tiếp theo cứ mỗi kilômét giá 11 000 đồng. Giả sử một người thuê xe đi x (kilômét).

a) Chứng tỏ rằng biểu thức biểu thị số tiền mà người đó phải trả là một đa thức. Tìm bậc, hệ số cao nhất và hệ số tự do của đa thức đó.

b) Giá trị của đa thức tại x=9 nói lên điều gì?

Giải nhanh:

a)  T(x)=8000+11000(x–0,5) =11 000x+2500

Bậc: 1; Hệ số cao nhất: 11000; Hệ số tự do: 2500

b)  T(9)=11000.9+2500=101500

 Giá trị của đa thức tại x=9 nói lên rằng nếu người đó thuê xe đi 9 km thì số tiền phải trả là 101500 đồng.

Bài tập 7.43: Cho đa thức bậc hai F(x)=a2+bx+c trong đó a, b và c là những số với a≠0.

a) Cho biết a+b+c=0. Giải thích tại sao x=1 là một nghiệm của F(x).

b) Áp dụng, hãy tìm một nghiệm của đa thức bậc hai 2−5x+3.

Giải nhanh:

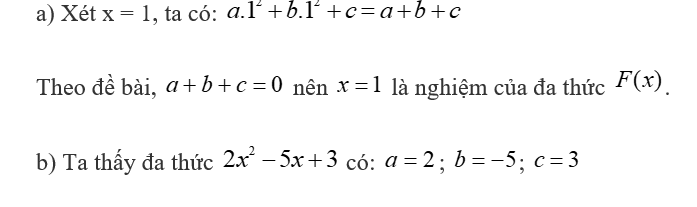
Mà a+b+c=0 =>  đa thức  có: Một nghiệm bằng 1; Nghiệm còn lại là c/a=3/2

Bài tập 7.44: Cho đa thức A=+−2x–2.

a) Tìm đa thức B sao cho A+B=+3x+1.

b) Tìm đa thức C sao cho A−C=

c) Tìm đa thức D, biết rằng D=(2x−3).A.

d) Tìm đa thức P sao cho A=(x+1).P.

e) Có hay không một đa thức Q sao cho A=(+1).Q.

Giải nhanh:

b) 

c) .

d) .

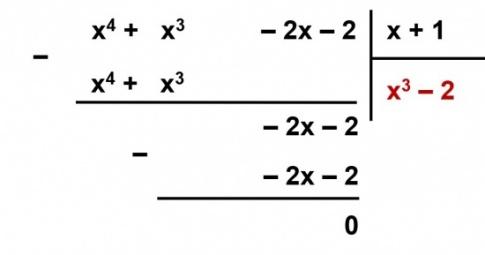
e) 

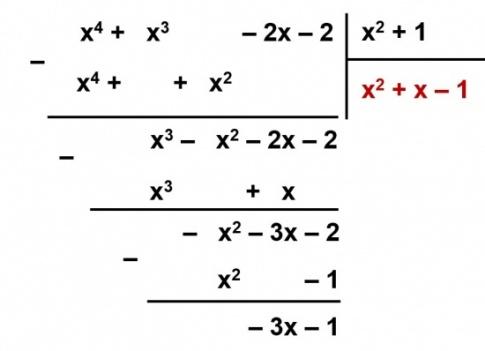
Đây là phép chia có dư nên đa thức Q không tồn tại.

Bài tập 7.45: Cho đa thức P(x). Giải thích tại sao nếu có đa thức Q(x) sao cho P(x)=(x−3).Q(x) (tức là P(x) chia hết cho x–3) thì x=3 là một nghiệm của P(x).

Giải nhanh:

P(x)=(x−3).Q(x)

Để P(x) = 0 thì:Q(x) = 0 hoặc (x−3)=0

- Ta có: x–3=0 => x=3 Nếu x=3 thì P(x)=0

Vậy: x=3 là một nghiệm của P(x).

Bài tập 7.46: Hai bạn Tròn và Vuông tranh luận với nhau như sau:

Hãy cho biết ý kiến của em và nêu một ví dụ minh họa.

Giải nhanh:

Theo em, ý kiến của bạn Tròn đúng.

Ví dụ: (4x⁴+x³)+(−4x⁴+1)=4x⁴+x³−4x⁴+1=(4x⁴–4x⁴)+x³+1=x³+1