BÀI TẬP CUỐI CHƯƠNG IV

Bài tập 4.33: Tính các số đo x, y trong tam giác dưới đây (H.4.75)

Giải nhanh:

.

Bài tập 4.34: Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng góc MAN = MBN

Giải nhanh:

Xét 2 tam giác MNA và MNB có: AM=BM; AN=BN; MN chung

=>ΔMNA=ΔMNB (c.c.c) => =

Bài tập 4.35: Trong Hình 4.77, có AO = BO, OAMˆ = OBNˆ. Chứng minh rằng AM = BN.

Giải nhanh:

Xét 2 tam giác OAM và OBN: = ; OA = OB; Góc O chung

=>  Δ OAM = ΔOBN      => AM =BN

Bài 4.36: Trong Hình 4.78, ta có AN = BM, = Chứng minh, =  

Giải nhanh:

Xét ΔBAN và ΔBMA, ta có : AN = BM; = ; AB chung

=> ΔBAN = ΔBMA (c-g-c) => =

Bài 4.37: Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Theo em, tứ giác AMBN là hình gì?

Giải nhanh:

Ta có . (c.c.c) vì:

, , là cạnh chung. Do đó, .

Bài 4.38: Cho tam giác ABC cân tại A có A = 120. Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:

a. ΔBAM = ΔCAN;

b. Các tam giác ANB, AMC lần lượt cân tại N, M.

Giải nhanh:

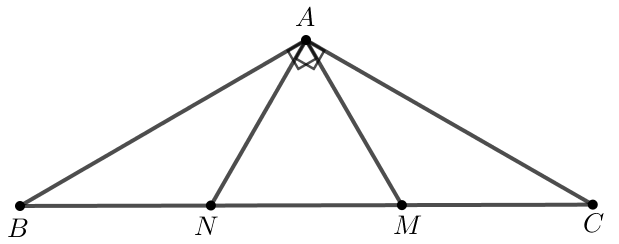
(cạnh góc vuông - góc nhọn) vì:

Ta có .

. Suy ra cân tại ;

. Suy ra cân tại .

Bài 4.39: Cho tam giác ABC vuông tại A có Trên cạnh BC lấy điểm M sao cho . Chứng minh rằng:

a. Tam giác CAM cân tại M;

b. Tam giác BAM là tam giác đều;

c. M là trung điểm của đoạn thẳng BC.

Giải nhanh:

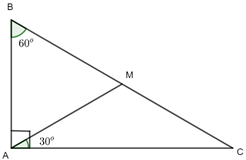
a) . Suy ra cân tại .

b) .

Vậy tam giác là tam giác đều.

c) , . => là trung điểm .