BÀI TẬP CUỐI CHƯƠNG IV

Bài tập 4.33: Tính các số đo x, y trong tam giác dưới đây...

Giải rút gọn:

3x + 30⁰ = 180⁰  => x = 50⁰

3y + 60⁰ = 180⁰ => y = 40⁰

Bài tập 4.34: Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh...

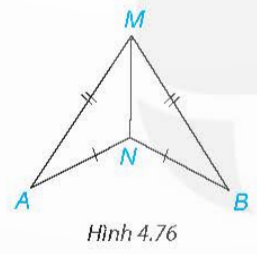
Giải rút gọn:

NA = NB, AM = MB , chung MN => ΔAMN = ΔBMN (c.c.c) => =

Bài tập 4.35: Trong Hình 4.77...

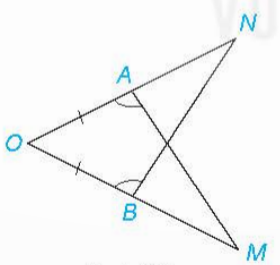
Giải rút gọn:

= , AO = BO , chung => ΔOAM = ΔOBN (g.c.g) => AM = BN

Bài 4.36: Trong Hình 4.78, ta có...

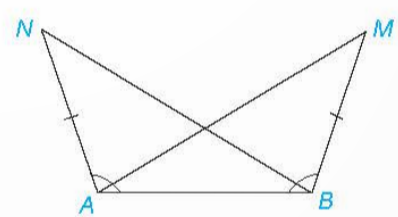
Giải rút gọn:

NA = MB, =, chung AB => ΔNAB = ΔMBA( c.g.c) => =

Bài 4.37: Cho M, N là hai điểm phân biệt nằm trên đường...

Giải rút gọn:

M, N đường trung trực của AB => AM = BM, AN = BN

Mà AM = AN (gt) => AM = AN = BM = BN

AM = AN , chung AB, MB = NB => ΔABM = ΔABN (c.c.c) => .

Bài 4.38: Cho tam giác ABC cân tại A có...

Giải rút gọn:

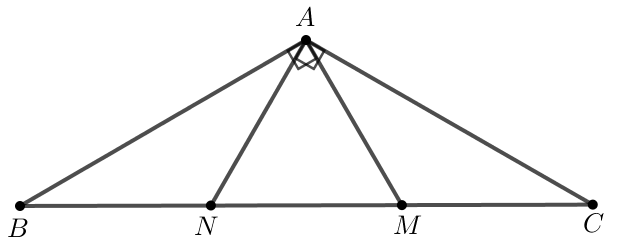
a) AB = AC , => ΔABM = ΔACN ( cạnh góc vuông – góc nhọn)

b) +) ΔABC có = (180⁰ – 120⁰) : 2 = 30⁰

   +) = 120⁰ – 90⁰ = 30⁰ = => ΔACM cân tại M

   +) = 120⁰ – 90⁰ = 30⁰ = => ΔBAN cân tại N

Bài 4.39: Cho tam giác ABC vuông tại A...

Giải rút gọn:

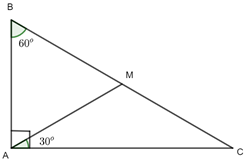
a) = 90⁰ – 60⁰ = 30⁰ = => ΔMAC cân tại M

b) = 90⁰ – 30⁰ = 60⁰

     = 180⁰ – 60⁰ - 60⁰ = 60⁰

     ΔBAM có 3 góc bằng 60⁰ => là tam giác đều

c) +) ΔBAM đều => MA = MB

   +) ΔCAM cân tại M => MA = MC

=> MB = MC hay M là trung điểm của BC.