BÀI 35. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TRỰC, BA ĐƯỜNG CAO TRONG MỘT TAM GIÁC

1. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TRỰC TRONG MỘT TAM GIÁC

Bài 1: Vẽ tam giác ABC...

Giải rút gọn:

3 đường trung trực cùng đi qua 1 điểm.

Bài 2: Dùng tính chất đường trung thực của một đoạn thẳng...

Giải rút gọn:

a) Gọi M là trung điểm của BC => OM⊥ BC

+) MB = MC, chung OM => ∆OBM = ∆ OCM(hai cạnh góc vuông) => OB = OC 

+) Chứng minh tương tự ta có : OA = AC

b) OB = OC; OA = OC => OA = OB => ∆OAB cân tại O

    kẻ ON ⊥ AB => ON đồng thời là đường trung tuyến => N là trung điểm AB

=> O thuộc đường trung trực của AB.

Bài 3: Chứng minh rằng trong tam giác đều ABC...

Giải rút gọn:

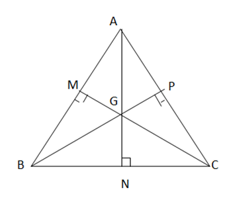
+) Kẻ 3 đường trung tuyến AN, BP, CM ; giao nhau tại G

+) AB = AC , NB = NC , chung AN => ∆ANB = ∆ ANC (c.c.c)

   => = => AG là đường phân giác

+) chứng minh tương tự ta có BG và CG là đường phân giác

=> G cách đều 3 cạnh ∆ABC

Mà G là trọng tâm => G là giao điểm 3 đường trung trực => G cách đều 3 đỉnh.

2. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG CAO TRONG MỘT TAM GIÁC

Bài 1: Vẽ tam giác ABC và 3 đường cao của nó...

Giải rút gọn:

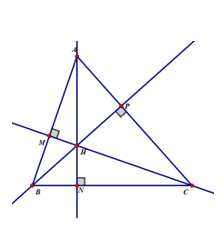
3 đường cao có đi qua 1 điểm 

Bài 2: a) Chứng minh trong tam giác ABC...

Giải rút gọn:

a)

Gọi AD là đường trung tuyến và đường phân giác

+) AB = AC , DB = DC , chung cạnh AD => ∆ADB = ∆ ADC (c.c.c)

=> = mà + =180^o => = = 90^o

=> AD ⊥ BC mà AD = BD => AD là trung trực 

b)

+) Gọi G là điểm cách đều 3 đỉnh . Kẻ GM ⊥ AB, GN ⊥ BC, GP ⊥ AC

+) GB = GC, AB = AC, chung AG => ∆AGB = ∆ AGC (c.c.c)

=> = => AG là đường phân giác của

+) Chứng minh tương tự ta có : BG, CG là đường phân giác

=> G là giao điểm 3 đường phân giác => G cách đều 3 cạnh ∆ABC

BÀI TẬP CUỐI SGK

Bài 9.26: Gọi H là trực tâm của tam giác ABC không vuông...

Giải rút gọn:

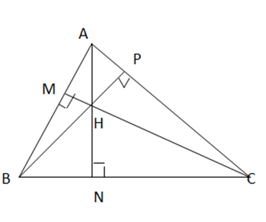
+) Kẻ đường cao AN, BP, CM

+) ΔAHB có CB ⊥ AH, CA ⊥ BH => C là trực tâm 

+) ΔAHC có BA ⊥ CH, BC ⊥ AH => B là trực tâm 

+) ΔCHB có AB ⊥ CH, AC ⊥ BH => A là trực tâm 

Bài 9.27: Cho tam giác ABC có...

Giải rút gọn:

+) Kẻ CE ⊥ AB, BF ⊥ AC, AD ⊥ BC

+) = , = (2 góc đối đỉnh)

=> + = + = = 100⁰

+) ΔHAE có : + = 90⁰ (1)

+) ΔHAF có : + = 90⁰ (2)

Từ (1) và (2) => + + + = 180⁰

                    <=>v( + ) + ( + ) = 180⁰

                     <=>100⁰ + = 180⁰ ó = 80⁰ hay = 80⁰

Bài 9.28: Xét điểm O cách đều 3 đỉnh của tam giác ABC...

Giải rút gọn:                     

+) OA = OB => ΔOAB cân tại O => = => = 180° -  2

+) OA = OC => ΔOAC cân tại O => = => = 180° -  2

+) Ta có : + = 180°

<=> 180° -  2 + 180° -  2 = 180°

<=> ( +    ) = 90⁰ ó = 90⁰ => ΔABC vuông tại A

Bài 9.29: a) Có một chi tiết máy...

Giải rút gọn:

a)

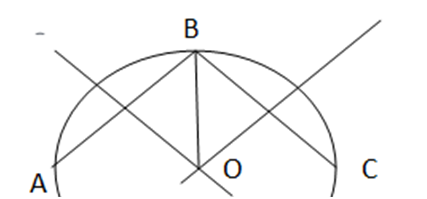
+) Lấy ba điểm phân biệt A, B, C trên đường viền ngoài

+) vẽ đường trung trực của 2 cạnh AB và BC; chúng cắt nhau tại O. O là điểm cần tìm

+) bán kính = OA = OB = OC

b)

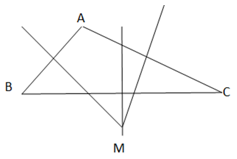
+) Vẽ đường trung trực của 3 cạnh AB, BC, AC; chúng cắt nhau tại M

+) MA = MB = MC => M là điểm cần tìm

Bài 9.30: Cho hai đường thẳng không vuông góc...

Giải rút gọn:

+) Kẻ HD ⊥ c ; HE ⊥ b

+) Lấy điểm B trên đường thẳng b sao cho E nằm giữa A và B

+) kẻ đường thẳng qua B và ⊥ AH, cắt c tại C.