BÀI 34. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TUYẾN, BA ĐƯỜNG PHÂN GIÁC TRONG MỘT TAM GIÁC

1. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TUYẾN TRONG MỘT TAM GIÁC

Bài 1: Trên mảnh giấy kẻ ô vuông, mỗi chiều 10 ô, hãy đếm dòng,đánh dấu các đỉnh A,B,C rồi vẽ tam giác ABC(H.9,29).Vẽ hai đường trung tuyến BN, CP, chúng cắt nhau tại G, tia AG cắt cạnh BC tại M.

• AM có phải đường trung tuyến của tam giác ABC không ?

• Hãy xác định các tỉ số GA/MA, GB/NB , GC/PC

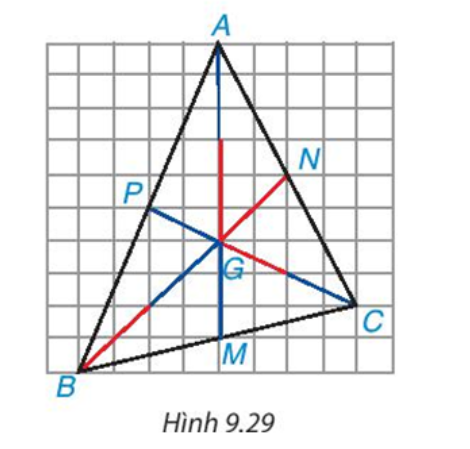
Giải nhanh:

• Ta có: MB = MC và M nằm giữa B và C 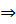  M là trung điểm của BC.

AM có là đường trung tuyến của tam giác ABC (định nghĩa)

Ta có:; ;

Bài 2: Trong tam giác ABC ở ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB.

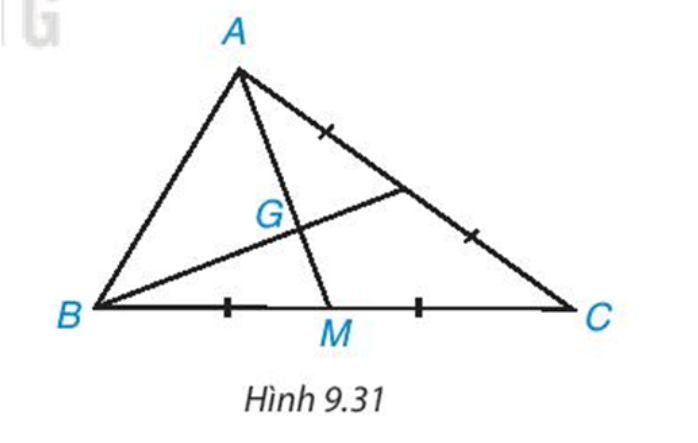
Giải nhanh:

Vì G là trọng tâm của ABC (gt)   hay GB = NB

Ta có: GN = NB – GB = NB - NB = NB

1 = NB NB = 3 cm

GB = NB = . 3 = 2 (cm).

2. SỰ ĐỒNG QUY CỦA BA ĐƯỜNG PHÂN GIÁC TRONG TAM GIÁC

Bài 1: Cho tam giác ABC có hai đường phân giác AM, BN cắt nhau tại điểm I. Hỏi CI có là đường phân giác của góc C không ?

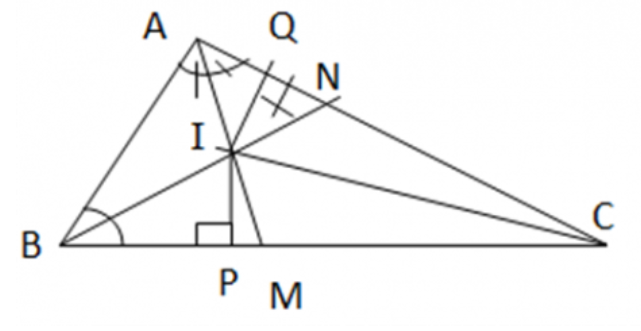
Giải nhanh:

Xét tam giác ABC có: AM là phân giá BN là phân giác; AM BN = {I}

CI cũng là đường phân giác của tam giác. 

Bài 2: Chứng minh rằng trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.

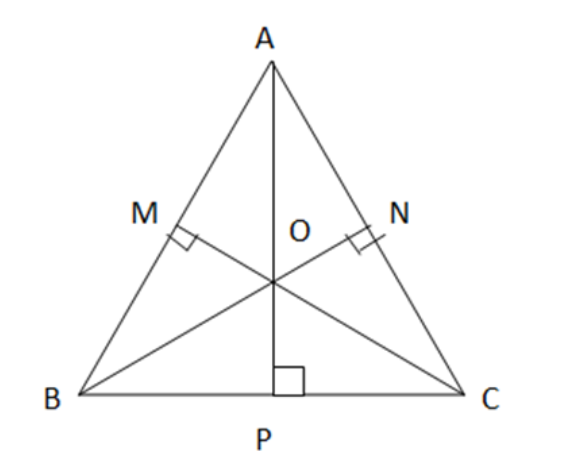
Giải nhanh:

Vì ΔABC đều AB = AC = BC 

Vì I cách đều 3 cạnh của tam giác I là giao điểm của 3 đường phân giác 

Áp dụng ví dụ 2, ta được, AI là đường trung tuyến của ΔABC

Tương tự, ta BI, CI là đường trung tuyến của ΔABC

Vậy I là trọng tâm của ΔABC.

BÀI TẬP CUỐI SGK

Bài 9.20: Cho tam giác ABC với hai đường trung tuyến BN,CP và trọng tâm G. Hãy tìm số thích hợp đặt vào dấu ''?'' để được các đẳng thức:

BG = ? BN, CG = ? CP; BG = ? GN, CG = ? GP

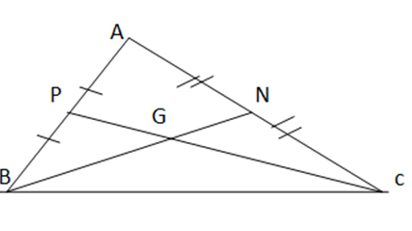
Giải nhanh:

G là trọng tâm của tam giác ABC=> CG =_2/3 CP => CG= 2 GP

Tương tự : BG = _2/3 BN => BG= 2 GN

Bài 9.21: Chứng minh rằng

a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau

b) Ngược lại nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân

Giải nhanh:

a) 

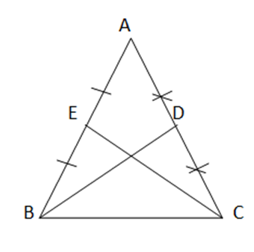
Ta có ∆ ABC cân tại A. BD và CE là trung tuyến với E là trung điểm của AB, D là trung điểm của AC

∆ ABC cân tại A => AB = AC

Có : AE = AB. AD= AC => AE= AD

Xét ∆ ABD và ∆ ACE ta có: chung; AE=AD; AB= AC

=> ∆ ABD  = ∆ ACE => BD= CE

b) 

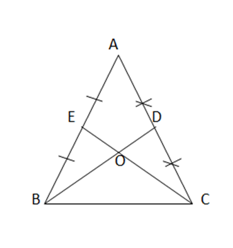
Gọi O là giao điểm của CE và BD

Ta có CE và BD là 2 đường trung tuyến nên O sẽ là trọng tâm của tam giác ∆ ABC 

=> BO = BD. OD= BD

      CO= CE. OE = CE;   CE= BD=> BO= CO. OD= OE

Xét ∆ EOB và ∆ DOC ta có: BO = OC; OD = OE; =  

=> ∆ EOB = ∆ DOC => EB= DC

Có EB = AB;   DC = AC => AB= AC => ∆ ABC cân tại A

Bài 9.22: Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN

Giải nhanh:

BM, CN là 2 đường trung tuyến cắt nhau tại 

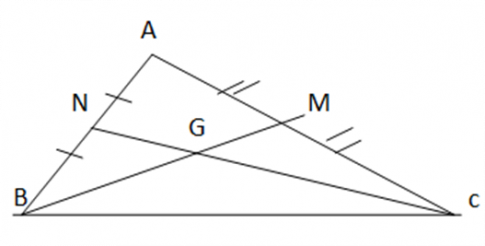
=> G là trọng tâm của tam giác ABC => BG= BM, CG= CN (1)

Trong tam giác GBC: > => CG > GB (2)

Từ (1) và (2) => CN > BM

Bài 9.23:  Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC = 120°

Giải nhanh:

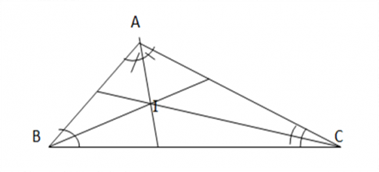
Có I là điểm đồng quy của ba đường phân giác trong tam giác ABC

AI, BI, CI lần lượt là đường phân giác của 3 góc , ,

= 120° => + = 60°

Ta có : =1/2 ; =1/2

2 + 2  = 60° => +   = 30°

Xét trong tam giác IBC ta có: +   + = 180°

=150°

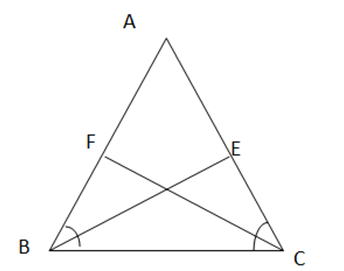
Bài 9.24: Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chúng minh BE= CF

Giải nhanh:

∆ABC cân tại A  => AB = AC. = (1)

BE là đường phân giác của => =1/2 (2)

CF là đường phân giác của => =1/2 (3)

Từ (1), (2), (3) => =

Xét ∆ ABE và ∆ ACF, ta có: chung; AB= AC; =

 =>  ∆ ABE = ∆ ACF => BE = CF

Bài 9.25: Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB

a) Hãy giải thích tại sao DP= DR

b) Hãy giải thích tại sao DP= DQ

c) Từ câu a và b suy ra DR= DQ. Tại sao D nằm trên tia phân giác của góc A 

Giải nhanh:

Ta có ∆ BPD và ∆ BRD đều là tam giác vuông tại và

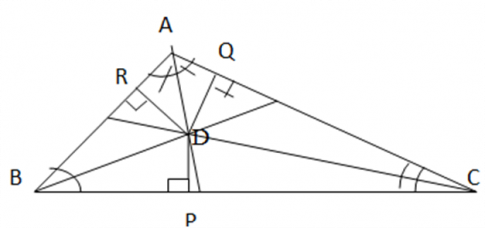
Xét 2 tam giác vuông là  ∆ BRD và ∆ BPD ta có: Chung cạnh BD

=  

∆ BRD = ∆ BPD => DR= DP

Ta có ∆ CPD và ∆ CQD đều là tam giác vuông tại và

Xét ∆ CPD và ∆ CQD ta có: Chung cạnh CD; =  

∆ CPD = ∆ CQD DP= DQ

Từ a và b ta có DR= DQ

Xét ∆ ARD và ∆ AQD ta có: Chung cạnh AD; DR= DQ

∆ ARD = ∆ AQD =   D nằm trên đường phân giác của