Câu 1: Phát biểu nào dưới đây đúng nhất?

• A. Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;                
• B. Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;   
• C. Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;                       

• D. Cả A, B, C đều đúng.

Câu 2: Cho ∆ABC có AB = AC ($\widehat{A}<90^{\circ}$). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB). Gọi I là giao điểm của BH và CK. Gọi D là giao điểm của AI và BC. Ta có các phát biểu sau:

(I) AI là tia phân giác của $\widehat{BAC}$

(II) AD ⊥ BC;

(III) D là trung điểm của BC.

Phát biểu đúng là:

• A. I và II;      
• B. II và III;   

• C. I và III;                

• D. I, II và III.

Câu 3: Cho hình vẽ dưới đây. Khẳng định đúng là

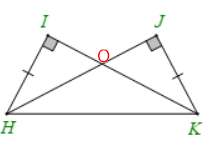
• A. ΔHIO=ΔOJK
• B. ΔIHO=ΔJOK
• C. ΔIHO=ΔKOJ

• D. ΔHIO=ΔKJO

Câu 4: Cho tam giác ABC vuông tại A và tam giác POI vuông tại I có BC = OP, $\widehat{C}=\widehat{P}$. Khẳng định sai là

• A. AB = IO;

• B. ΔABC=ΔPOI

• C. $\widehat{B}=\widehat{O}$
• D. ΔABC=ΔIOP

Câu 5: Cho ∆ABC vuông tại A có AB < AC. Kẻ AH vuông góc với BC (H ∈ BC). Gọi D là điểm trên cạnh AC sao cho AD = AB. Vẽ DE vuông góc với BC (E ∈ BC) và DK vuông góc với AH (K ∈ AH). Độ dài của HE bằng:

• A. HA;                       
• B. KD;                       

• C. Cả A và B đều đúng;              

• D. Cả A và B đều sai.

Câu 6: Cho tam giác ABC vuông tại B và tam giác PMN vuông tại M có AC = PN, $\widehat{A}=\widehat{P}$. Biết AB = 4 cm; AC = 5 cm. Chu vi tam giác PMN là 14 cm. Diện tích tam giác PMN là

• A. 12 cm$^{2}$;

• B. 10 cm$^{2}$;

• C. 6 cm$^{2}$;
• D. 7,5 cm$^{2}$.

Câu 7: Cho tam giác ABC và DEF có : $\widehat{B}=\widehat{E}=90°, AB = EF, \widehat{A}=\widehat{F}$. Phát biểu nào sau đây đúng

• A. ΔABC = ΔFED

• B. ΔABC = ΔFDE
• C. ΔBAC = ΔFED
• D. ΔABC = ΔDEF

Câu 8: Cho đoạn thẳng AB, điểm O nằm giữa A và B. Kẻ tia Ox vuông góc với AB. Trên tia Ox lấy các điểm C và D sao cho OC = OA, OD = OB. Gọi M, N lần lượt là trung điểm của AD và BC. Góc MON là:

• A. góc nhọn;                      

• B. góc vuông;                    

• C. góc tù;                 
• D. góc bẹt.

Câu 9: Cho ∆ABC có AB = AC ($\widehat{A}<90^{\circ}$). Kẻ BD vuông góc với AC (D ∈ AC) và CE vuông góc với AB (E ∈ AB). Gọi H là giao điểm của BD và CE.  

Cho bảng sau:

Ghép các ý ở cột A với cột B để được một đẳng thức đúng?

• A. a – 2; b – 1; c – 3;                    
• B. a – 1; b – 3; c – 2;                    

• C. a – 3; b – 1; c – 2;                    

• D. a – 2; c – 1; b – 3.

Câu 10: Cho ∆ABC có AB = AC. Gọi AM là tia phân giác của $\widehat{A}$ (M ∈ BC). Kẻ MD vuông góc AB (D ∈ AB) và ME vuông góc với AC (E ∈ AC).

Cho các khẳng định sau:

(I) $\widehat{BMD}=\widehat{CME}$

(II) ∆MBD = ∆MCE

(III) AD = AE

Gọi m là số kết luận đúng và n là số kết luận sai. Giá trị của m và n là:

• A. m = 0 và n = 1;            
• B. m = 2 và n = 1;            

• C. m = 3 và n = 0;             

• D. m = 1 và n = 2.

Câu 11: Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Kết luận nào sau đây sai?

• A. AM = DM;                      
• B. ∆ABM = ∆ADM ;                     
• C. $\widehat{MAD}=\widehat{MDA}$

• D. A, B, C sai.

Câu 12: Cho ∆ABC vuông tại B và ∆DEF vuông tại E có AB = DE và BC = EF. Khi đó ∆ABC = ∆DEF theo trường hợp:

• A. cạnh huyền – cạnh góc vuông;                 
• B. cạnh huyền – góc nhọn;                  

• C. cạnh – góc – cạnh;                  

• D. góc – cạnh – góc.

Câu 13: Cho tam giác ABC có AD vuông góc với BC. Biết AB = AC = 3cm, $\widehat{A}=60^{\circ}$ . Tính cạnh BC.

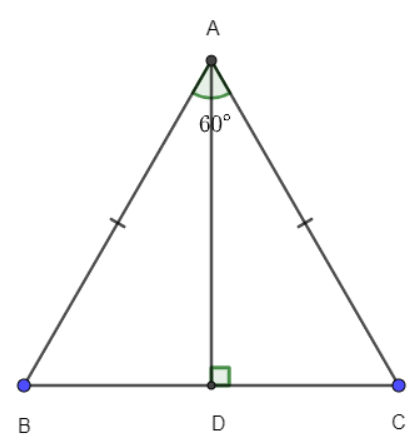
• A. BC = 6 cm;                     
• B. BC = 1,5 cm;                 
• C. BC = 9 cm;                     

• D. BC = 3cm.

Câu 14: Trong các phương án sau, phương án nào chứa hình có hai tam giác vuông không bằng nhau?

• A. 
• B. 
• C. 

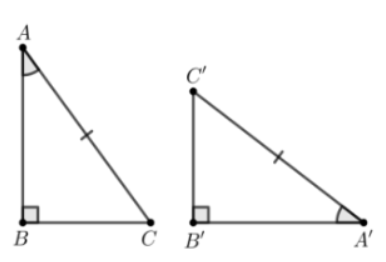
• D. 

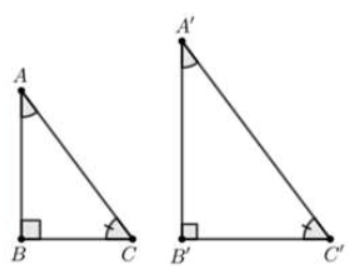
Câu 15: Cho hình vẽ bên.

Khẳng định nào sau đây sai?

• A. ∆AED = ∆AFD;             
• B. ∆BED = ∆CFD;             
• C. ∆ADB = ∆ADC;             

• D. ∆ADE = ∆AFD.

Câu 16: Cho tam giác ABC vuông tại B và tam giác MNP vuông tại N, có AB = MN. Cần thêm điều kiện gì để ΔABC=ΔMNP theo trường hợp cạnh huyền - cạnh góc vuông?

• A. AC = MP;

• B. $\widehat{A}=\widehat{M}$
• C. BC = MP;
• D. BC = NP.

Câu 17: Cho ∆MNP vuông tại P và ∆XYZ vuông tại Z có MP = XZ. Để ∆MNP = ∆XYZ theo trường hợp cạnh huyền – cạnh góc vuông thì cần thêm điều kiện gì?

• A. MN = XY;                       

• B. MN = YZ;          
• C. $\widehat{NMP}=\widehat{ZYX}$
• D. $\widehat{MNP}=\widehat{XYZ}$

Câu 18: Cho ∆ABC có AB = AC và $\widehat{B}=\widehat{C}$ Trên cạnh BC, lấy hai điểm D và E sao cho BD = EC. Kẻ DM vuông góc với AB (M ∈ AB) và EN vuông góc với AC (N ∈ AC). Kết luận nào sau đây đúng nhất?

• A. ∆AMD = ∆ANE;                       
• B. ∆ABD = ∆ACE;             
• C. MD = EN;                       

• D. Cả A, B, C đều đúng.

Câu 19: Cho ∆ABC và ∆PQR. Giả thiết nào dưới đây không suy ra được ∆ABC = ∆PQR?

• A. $\widehat{A}=\widehat{P}=90^{\circ},\widehat{B}=\widehat{Q},\widehat{C}=\widehat{R}$

• B. $\widehat{A}=\widehat{P}=90^{\circ},\widehat{B}=\widehat{Q},AB = PQ$
• C. $\widehat{A}=\widehat{P}=90^{\circ},BC=QR,\widehat{C}=\widehat{R}$
• D. $\widehat{A}=\widehat{P}=90^{\circ},BC=QR,AC=PR$

Câu 20: Cho đoạn thẳng BC và điểm H nằm giữa B và C. Qua H kẻ đường thẳng vuông góc với BC. Trên đường thẳng đó lấy các điểm A và K sao cho HA = HK. Kẻ các đoạn thẳng AB, BK, KC, CA. Kết luận nào sau đây sai?

• A. BA = BK;            

• B. $\widehat{ABC}>\widehat{KBC}$

• C. $\widehat{BAK}=\widehat{BKA}$
• D. ∆AHB = ∆KHB.