Lý thuyết trọng tâm toán 7 kết nối bài 15: Các trường hợp bằng nhau của tam giác vuông
Tổng hợp kiến thức trọng tâm toán 7 kết nối tri thức bài 15 Các trường hợp bằng nhau của tam giác vuông. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
BÀI 15. CÁC TRƯỜNG HỢP BẰNG NHAU CỦA TAM GIÁC VUÔNG
1. BA TRƯỜNG HỢP BẰNG NHAU CỦA TAM GIÁC VUÔNG.
HĐ1:
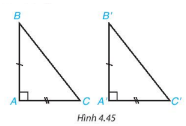
Xét tam giác ABC và A’B’C’ có:
AB = A’B’
$\widehat{BAC}$=$\widehat{B'A'C'}$
AC = A’C’
⇒ΔABC=ΔA'B'C' (c.g.c)
Định lí 1:
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
GT | ΔABC,ΔA'B'C'. $\widehat{BAC}$=$\widehat{B'A'C'}$=90$^{\circ}$ AB = A’B’, AC = A’C’ |
KL | ΔABC=ΔA'B'C' |
HĐ2:
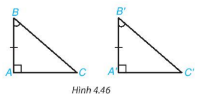
Xét tam giác ABC và A’B’C’ có:
$\widehat{BAC}$=$\widehat{B'A'C'}$
AB = A’B’
$\widehat{ABC}$=$\widehat{A'B'C'}$
ΔABC=ΔA'B'C' (g.c.g)
Định lí 2:
Nếu một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
GT | ΔABC,ΔA'B'C'. $\widehat{BAC}$=$\widehat{B'A'C'}$=90 AB = A’B’, $\widehat{ABC}$=$\widehat{A'B'C'}$ |
KL | ΔABC=ΔA'B'C' |
Luyện tập 1:
Hai tam giác vuông này bằng nhau vì có một cặp cạnh góc vuông kề với chúng bằng nhau.
Lí do bạn Tròn đưa ra là chính xác.
HĐ3:
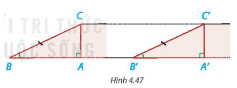
a) $\widehat{C}$=90$^{\circ}$-$\widehat{B}$=90$^{\circ}$-$\widehat{B'}$=$\widehat{C'}$.
Xét tam giác ABC và A’B’C’ có:
$\widehat{ABC}$=$\widehat{A'B'C'}$
BC = B’C’
$\widehat{ACB}$=$\widehat{A'C'B'}$
ΔABC=ΔA'B'C' (g.c.g)
b) AC = A’C’ (ΔABC=ΔA'B'C')
Do đó độ cao của hai con dốc này bằng nhau.
Định lí 3:
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
GT | ΔABC,ΔA'B'C'. $\widehat{BAC}$=$\widehat{B'A'C'}$'=90$^{\circ}$, BC = B’C’; $\widehat{ACB}$=$\widehat{A'C'B'}$ |
KL | ΔABC=ΔA'B'C' |
Câu hỏi:
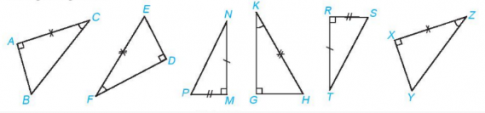
ΔABC=ΔXYZ (cạnh góc vuông – góc nhọn)
ΔDEF=ΔGHK (cạnh huyền – góc nhọn)
ΔMNP=ΔRTS (hai cạnh góc vuông).
Ví dụ 1 (SGK – tr77)
Luyện tập 2:
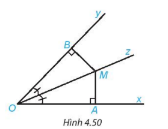
Xét hai tam giác vuông OMA và OMB có:
OM là cạnh chung
$\widehat{MOB}$=$\widehat{MOA}$
⇒ΔOMA=ΔOMB (cạnh huyền – góc nhọn).
2. TRƯỜNG HỢP ĐẶC BIỆT CỦA TAM GIÁC VUÔNG
HĐ4:
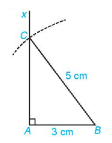
HĐ5:
a) AC = A’C’
b) Hai tam giác vuông ABC và A’B’C’ bằng nhau (cặp cạnh góc vuông bằng nhau).
Định lí:
Nếu cạnh huyền và một góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
GT | ΔABC,ΔA'B'C'. $\widehat{BAC}$=$\widehat{B'A'C'}$=90$^{\circ}$, BC = B’C’; AB = A’B’ |
KL | ΔABC=ΔA'B'C' |
Câu hỏi:
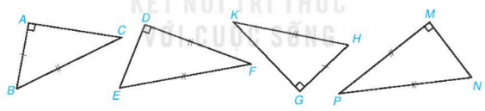
+ Xét tam giác ABC và GHK có:
AB = GH
BC = HK
Suy ra ΔABC=ΔGHK (cạnh huyền – cạnh góc vuông)
+ Tương tự ΔDEF=ΔMNP
Ví dụ 2 (SGK – tr78)
Luyện tập 3:
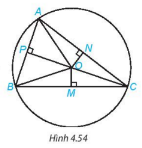
+ Xét tam giác OAP và OBP có:
OA = OB; OP chung
⇒ΔOAP=ΔOBP (cạnh huyền – cạnh góc vuông).
+ Tương tự có ΔOAN=ΔOCN (cạnh huyền – cạnh góc vuông) vì OA = OC, ON chung.
+ ΔOBM=ΔOCM (cạnh huyền – cạnh góc vuông) vì OB = OC, OM chung.
Thử thách nhỏ:
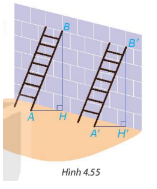
ΔHAB=ΔH'A'B' (cạnh huyền – cạnh góc vuông) vì:
AB = A’B’, HB = H’B’
Vậy $\widehat{HAB}$=$\widehat{H'A'B'}$.
Bình luận