CHƯƠNG 1: PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH

BÀI 3: GIẢI HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Bài tập 1 trang 13 sách bài tập Toán 9 Tập 1: Giải các hệ phương trình:

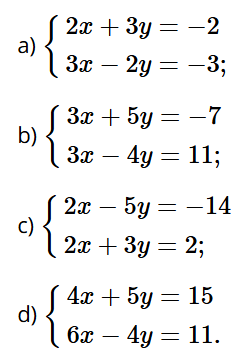
Bài giải chi tiết: 

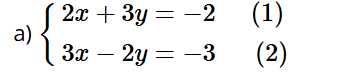
Nhân hai vế của phương trình (1) với 3 và nhân hai vế của phương trình (2) với ‒2 ta được: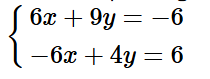

Cộng từng vế hai phương trình của hệ, ta được: 13y = 0, suy ra y = 0.

Thay y = 0 vào phương trình (1), ta được: 2x + 3.0 = –2. Do đó x = –1.

Vậy hệ phương trình có nghiệm duy nhất là (–1; 0).

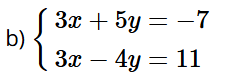
Trừ từng vế của phương trình thứ nhất và phương trình thứ hai của hệ, ta được:

9y = –18, suy ra y = –2.

Thay y = –2 vào phương trình thứ hai của hệ, ta được:

3x – 4.(–2) = 11 hay 3x + 8 = 11. Do đó x = 1.

Vậy hệ phương trình có nghiệm duy nhất là (1; –2).

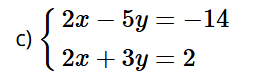
Trừ từng vế của phương trình thứ hai và phương trình thứ nhất của hệ, ta được:

8y = 16, suy ra y = 2.

Thay y = 2 vào phương trình thứ hai của hệ, ta được:

2x + 3.2 = 2 hay 2x + 6 = 2. Do đó x = –2.

Vậy hệ phương trình có nghiệm duy nhất là (–2; 2).

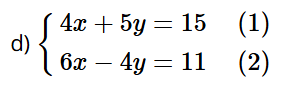
Nhân hai vế của phương trình (1) với 3 và nhân hai vế của phương trình (2) với ‒2 ta được: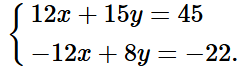

ộng từng vế hai phương trình của hệ trên, ta được: 23y = 23, suy ra y = 1.

Thay y = 1 vào phương trình (2), ta được:

6x – 4.1 = 11 hay 6x – 4 = 11, do đó x =

Vậy hệ phương trình có nghiệm duy nhất là (

Bài tập  2 trang 14 sách bài tập Toán 9 Tập 1: Giải các hệ phương trình:

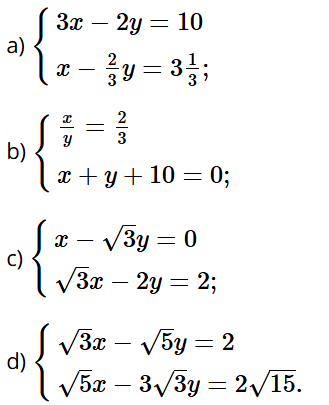
Bài giải chi tiết: 

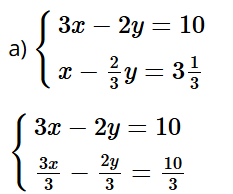
Nhân hai vế của phương trình thứ hai của hệ với 3, ta được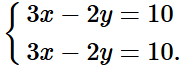

Trừ từng vế phương trình thứ nhất và phương trình thứ hai của hệ, ta được:

0x = 0. Phương trình này nghiệm đúng với mọi x ∈ ℝ.

Vậy hệ phương trình có vô số nghiệm. Các nghiệm của hệ được viết như sau: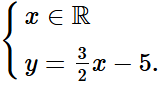 

b) Điều kiện: y ≠ 0.

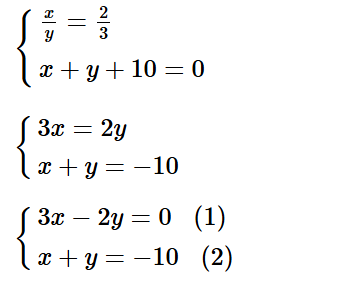
Từ phương trình (2), ta có: y = – 10 – x. (3)

Thay y = – 10 – x vào phương trình (1), ta được: 3x – 2.(–10 – x) = 0. (4)

Giải phương trình (4):

3x – 2.(–10 – x) = 0

3x + 20 + 2x = 0

5x = –20

x = –4.

Thay x = –4 vào phương trình (3), ta được: y = –10 – (–4) = –6.

Vậy hệ phương trình có nghiệm duy nhất là (–4; –6).

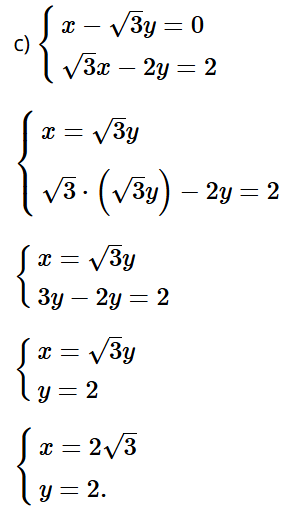
Bài tập 3 trang 14 sách bài tập Toán 9 Tập 1: Xác định a, b để đồ thị hàm số y = ax + b đi qua hai điểm A và B trong mỗi trường hợp sau:

a) A(1; 1) và B(3; 7);

b) A(2; 1) và B(4; –3).

Bài giải chi tiết: 

Do đồ thị hàm số y = ax + b đi qua hai điểm A và B nên tọa độ của hai điểm A và B thỏa mãn hàm số y = ax + b.

a) Thay toạ độ điểm A(1; 1) và B(3; 7) vào hàm số y = ax + b, ta được hệ phương trình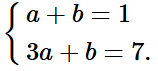

Giải hệ phương trình: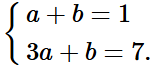

Trừ từng vế của phương trình thứ hai và phương trình thứ nhất của hệ, ta được:

2a = 6, suy ra a = 3.

Thay a = 3 vào phương trình thứ nhất của hệ, ta được:

3 + b = 1, do đó b = –2.

Vậy a = 3, b = –2.

b) Thay toạ độ điểm A(2; 1) và B(4; –3) vào hàm số y = ax + b, ta được hệ phương trình: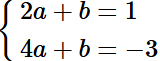

Giải hệ phương trình: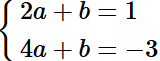

Trừ từng vế của phương trình thứ hai và phương trình thứ nhất của hệ, ta được:

2a = –4, suy ra a = –2.

Thay a = –2 vào phương trình thứ nhất của hệ, ta được:

4.(–2) + b = –3, hay –8 + b = –3, do đó b = 5.

Vậy a = –2, b = 5.

Bài tập 4 trang 14 sách bài tập Toán 9 Tập 1: Trong tháng 9, hai tổ sản xuất được 1 100 chi tiết máy. Sang tháng 10, tổ Một sản xuất vượt mức 15%, tổ Hai sản xuất vượt mức 20% so với tháng 9, do đó tháng 10 hai tổ sản xuất được 1 295 chi tiết máy. Hỏi trong tháng 9 mỗi tổ sản xuất được bao nhiêu chi tiết máy?

Bài giải chi tiết: 

Gọi x, y lần lượt là số chi tiết máy tổ Một và tổ Hai sản xuất được trong tháng 9 (x ∈ ℕ*, y ∈ ℕ*).

Số chi tiết máy hai tổ sản xuất được trong tháng 9 là: x + y (chi tiết máy).

Do trong tháng 9, hai tổ sản xuất được 1 100 chi tiết máy nên ta có phương trình:

Số chi tiết máy tổ 1 sản xuất trong tháng 10 là: x + 15%x = 1,15x (chi tiết máy).

Số chi tiết máy tổ 2 sản xuất trong tháng 10 là: y + 20%y = 1,2y (chi tiết máy).

Do tháng 10 hai tổ sản xuất được 1 295 chi tiết máy nên ta có phương trình:

1,15x + 1,2y = 1 295. (2)

Từ (1) và (2) ta có hệ phương trình: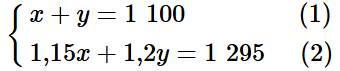

Cộng từng vế hai phương trình của hệ, ta được:

0,05y = 30, suy ra y = 600.

Thay y = 600 vào phương trình (1) ta được: x + 600 = 1 100. Do đó x = 500.

Ta thấy x = 500, y = 600 thoả mãn điều kiện.

Vậy trong tháng 9, tổ Một sản xuất được 500 chi tiết máy, tổ Hai sản xuất được 600 chi tiết máy.

Bài tập 5 trang 14 sách bài tập Toán 9 Tập 1: Một ô tô di chuyển trên quãng đường AB với tốc độ 60 km/h, rồi tiếp tục di chuyển trên quãng đường BC với tốc độ 55 km/h. Biết tổng chiều dài quãng đường AB và BC là 200 km và thời gian ô tô đi hết quãng đường AB ít hơn thời gian đi hết quãng đường BC là 30 phút. Tính thời gian ô tô di chuyển hết mỗi quãng đường.

Bài giải chi tiết: 

Đổi 30 phút = 0,5 giờ.

Gọi x (giờ) và y (giờ) lần lượt là thời gian ô tô di chuyển hết quãng đường AB và BC (x > 0, y > 0).

Do thời gian ô tô đi hết quãng đường AB ít hơn thời gian đi hết quãng đường BC là 30 phút nên ta có y – x = 0,5 hay x – y = –0,5. (1)

Quãng đường AB ô tô di chuyển với tốc độ 60 km/h là: 60x (km).

Quãng đường BC ô tô di chuyển với tốc độ 55 km/h là: 55y (km).

Tổng chiều dài quãng đường AB và BC là:

60x + 55y = 200 hay 12x + 11y = 40. (2)

Từ (1) và (2) ta có hệ phương trình: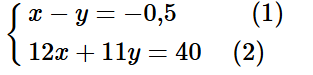

Nhân hai vế của phương trình (1) với 12, ta được: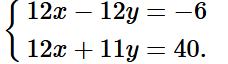

Trừ từng vế của phương trình thứ hai và phương trình thứ nhất, ta được:

23y = 46, suy ra y = 2.

Thay y = 2 vào phương trình (1), ta được: x – 2 = –0,5, do đó x = 1,5.

Ta thấy x = 1,5 và y = 2 (thoả mãn điều kiện).

Đổi x = 1,5 (giờ) = 1 giờ 30 phút.

Vậy thời gian di chuyển hết quãng đường AB là 1 giờ 30 phút, thời gian ô tô di chuyển hết quãng đường BC là 2 giờ.

Bài tập 6 trang 14 sách bài tập Toán 9 Tập 1: Một mảnh vườn hình chữ nhật có chu vi 360 m. Biết chiều dài của mảnh vườn bằng lần chiều rộng. Tính chiều dài và chiều rộng của mảnh vườn.

Bài giải chi tiết: 

Gọi x (m), y (m) lần lượt là chiều dài và chiều rộng của mảnh vườn (x > 0, y > 0).

Chu vi mảnh vườn là 360 m, nên nửa chu vi của mảnh vườn là: 360 : 2 = 180 (m).

Do đó, ta có phương trình: x + y = 180. (1)

Mảnh vườn có chiều dài bằng lần chiều rộng nên ta có phương trình:

x = hay 4x – 5y = 0. (2)

Từ (1) và (2), ta có hệ phương trình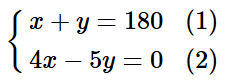

Cộng từng vế hai phương trình của hệ trên, ta được:

‒9y = ‒720, suy ra y = 80.

Thay y = 80 vào phương trình (1), ta được:

x + 80 = 180, do đó x = 100.

Ta thấy x = 100, y = 80 thoả mãn điều kiện.

Vậy chiều dài của mảnh vườn là 100 m, chiều rộng của mảnh vườn là 80 m.

Bài tập 7 trang 14 sách bài tập Toán 9 Tập 1: Để tổ chức tham quan khu di tích Bến Nhà Rồng (Thành phố Hồ Chí Minh) cho 195 người gồm học sinh khối lớp 9 và giáo viên phụ trách, nhà trường đã thuê 5 chiếc xe gồm hai loại: loại 45 chỗ và loại 30 chỗ. Hỏi nhà trường cần thuê bao nhiêu xe mỗi loại để chở hết số người đó? (Biết rằng trường mong muốn các xe không còn chỗ trống.)

Bài giải chi tiết: 

Gọi x (xe) và y (xe) lần lượt là số xe loại 45 chỗ và 30 chỗ (x ∈ ℕ*, y ∈ ℕ*).

Do nhà trường đã thuê 5 chiếc xe gồm hai loại 45 chỗ và 30 chỗ nên ta có:

x + y = 5. (1)

Số người ngồi trên các xe 45 chỗ là: 45x (người).

Số người ngồi trên các xe 30 chỗ là: 30y (người).

Do có tất cả 195 người chia vào tất cả các xe nên ta có: 45x + 30y = 195. (2)

Từ (1) và (2), ta có hệ phương trình: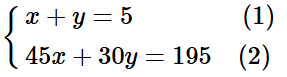

Nhân hai vế của phương trình (1) với ‒45, ta được: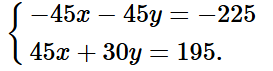

Cộng từng vế hai phương trình của hệ, ta được: ‒15y = ‒30, suy ra y = 2.

Thay y = 2 vào phương trình (1), ta được: x + 2 = 5, do đó x = 3.

Ta thấy x = 3 và y = 2 thoả mãn điều kiện.

Vậy nhà trường cần thuê 3 xe loại 45 chỗ và 2 xe loại 30 chỗ.

Bài tập 8 trang 14 sách bài tập Toán 9 Tập 1: Một vật là hợp kim của đồng và kẽm có khối lượng 124 g và thể tích 15 cm³. Tính xem trong đó có bao nhiêu gam đồng và bao nhiêu gam kẽm, biết rằng cứ 89 g đồng thì có thể tích là 10 cm³ và 7 g kẽm có thể tích là 1 cm³.

Bài giải chi tiết: 

Gọi x (g) và y (g) lần lượt là số gam đồng và kẽm có trong vật đó (0 < x, y < 124).

Vì khối lượng của vật là 124 g nên ta có phương trình x + y = 124. (1)

Thể tích của x (g) đồng là

Thể tích của y (g) kẽm là

Vì thể tích của vật là 15 cm³ nên ta có phương trình +

Từ (1) và (2) ta có hệ phương trình: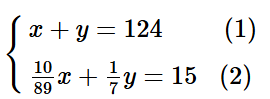

Nhân hai vế của phương trình (2) với 7, ta được: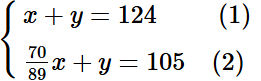

Trừ từng vế phương trình (1) và phương trình (2) của hệ, ta được:

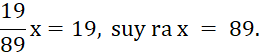
Thay x = 89 vào phương trình (1), ta được: 89 + y = 124, do đó y = 35.

Ta thấy x = 89, y = 35 thoả mãn điều kiện.

Vậy vật đó có 89 g đồng và 35 g kẽm.