CHƯƠNG 1: PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH

BÀI TẬP CUỐI CHƯƠNG 1

Bài tập 1 trang 15 sách bài tập Toán 9 Tập 1: Nghiệm của phương trình 

(x + 5)(2x – 10) = 0 là

A. x = –5 hoặc x = 5.

B. x = 5.

C. x = –5.

D. x ≠ 5.

Bài giải chi tiết: 

Đáp án đúng là: A

Ta có:

(x + 5)(2x – 10) = 0

x + 5 = 0 hoặc 2x ‒ 10 = 0

x = ‒5 hoặc x = 5.

Vậy phương trình đã cho có hai nghiệm là x = –5 và x = 5.

Bài tập 2 trang 15 sách bài tập Toán 9 Tập 1: Điều kiện xác định của phương trình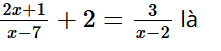

A. x ≠ 7.

B. x ≠ 2.

C. x ≠ 7 và x ≠ 2.

D. x = 7 và x = 2.

Bài giải chi tiết: 

Đáp án đúng là: C

Điều kiện xác định của phương trình là x ‒ 7 ≠ 0 và x ‒ 2 ≠ 0, hay x ≠ 7 và x ≠ 2.

Bài tập 3 trang 15 sách bài tập Toán 9 Tập 1: Nghiệm của phương trình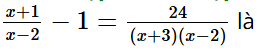

A. x = 2.

B. x = 5.

C. x = –3.

D. x = –5.

Bài giải chi tiết: 

Điều kiện xác định của phương trình là: x + 3 ≠ 0 và x ‒ 2 ≠ 0, hay x ≠ 2

và x ≠ ‒3.

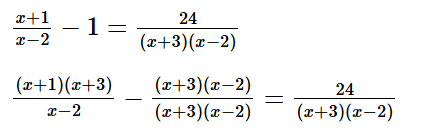
(x + 1)(x + 3) – (x + 3)(x – 2) = 24

x² + 3x + x + 3 ‒ x² + 2x ‒ 3x + 6 = 24

3x = 15

x = 5 (thỏa mãn điều kiện).

Vậy phương trình có nghiệm x = 5.

Bài tập 4 trang 15 sách bài tập Toán 9 Tập 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn?

A. 2x² + 2 = 0.

B. 3y – 1 = 5(y – 2).

C. 2x + = 0.

D. 3+ = 0.

Bài giải chi tiết: 

Đáp án đúng là: C

Phương trình bậc nhất hai ẩn x và y là hệ thức có dạng ax + by = c, trong đó a, b, c là các số đã biết (gọi là hệ số), a và b không đồng thời bằng 0.

Ta viết phương trình 2x + thành 2x + nên phương trình này là phương trình bậc nhất hai ẩn x và y với các hệ số a = 2; b = ; c = 1.

Bài tập 5 trang 15 sách bài tập Toán 9 Tập 1: Đường thẳng biểu diễn tất cả các nghiệm của phương trình 2x – y = 1 có đặc điểm nào sau đây?

A. Vuông góc với trục hoành.

B. Vuông góc với trục tung.

C. Đi qua gốc toạ độ.

D. Đi qua điểm A(1; 1).

Bài giải chi tiết: 

Đáp án đúng là: D

Ta viết phương trình 2x – y = 1 thành y = 2x ‒ 1. Do đó đường thẳng biểu diễn các nghiệm của phương trình không vuông góc với trục hoành, không vuông góc với trục tung.

Xét điểm A(1; 1): thay x = 1 vào phương trình y = 2x ‒ 1 ta được:

y = 2.1 ‒ 1 = 1.

Do đó đường thẳng biểu diễn tất cả các nghiệm của phương trình 2x – y = 1 đi qua A(1; 1).

Vậy ta chọn phương án D.

Bài tập 6 trang 15 sách bài tập Toán 9 Tập 1: Cặp số (3; –1) là nghiệm của hệ phương trình nào sau đây?

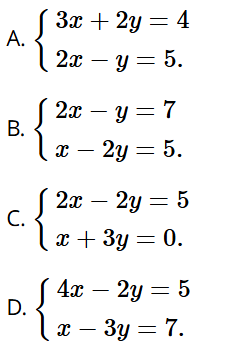
Bài giải chi tiết: 

Đáp án đúng là: B

Cặp số (3; –1) là nghiệm của hệ phương trình vì 

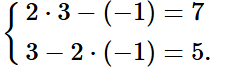
Bài tập 7 trang 16 sách bài tập Toán 9 Tập 1: Cho phương trình 2x + y = 3.

a) Cặp số (3; –3) là một nghiệm của phương trình đã cho.

b) Phương trình đã cho chỉ có một nghiệm.

c) Phương trình đã cho có vô số nghiệm.

d) Tất cả nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng y = –2x + 3.

Bài giải chi tiết: 

– Cặp số (3; –3) là một nghiệm của phương trình đã cho vì 2.3 + (‒3) = 3.

Do đó ý a) là đúng.

– Phương trình 2x + y = 3 viết lại thành y = – 2x + 3.

⦁ Với mỗi giá trị của x, ta sẽ có một giá trị y tương ứng. Do đó phương trình đã cho có vô số nghiệm. Khi đó, ý b) là sai và ý c) là đúng.

⦁ Tất cả nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng y = –2x + 3.

Do đó ý d) là đúng.

Vậy: a) Đúng.

b) Sai.

c) Đúng.

d) Đúng.

Bài tập 8 trang 16 sách bài tập Toán 9 Tập 1: Cho phương trình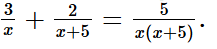

 a) Điều kiện xác định của phương trình đã cho là x ≠ 0 hoặc x ≠ –5.

b) Điều kiện xác định của phương trình đã cho là x ≠ 0 và x ≠ –5.

c) Nghiệm của phương trình đã cho là x = –2.

d) Nghiệm của phương trình đã cho là x = 2.

Bài giải chi tiết: 

Xét phương trình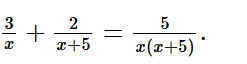

⦁ Điều kiện xác định của phương trình đã cho là x ≠ 0 và x + 5 ≠ 0, hay x ≠ 0 và x ≠ ‒5.

Do đó ý a) sai và ý b) đúng.

⦁ Giải phương trình:

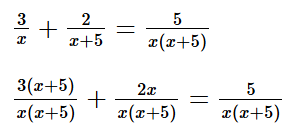
3(x + 5) + 2x = 5

3x + 15 + 2x = 5

5x = ‒10

x = ‒2.

Như vậy, nghiệm của phương trình đã cho là x = –2.

Do đó ý c) đúng và ý d) sai.

Vậy: a) Sai.

b) Đúng.

c) Đúng.

d) Sai.

Bài tập 9 trang 16 sách bài tập Toán 9 Tập 1: Cho hệ phương trình: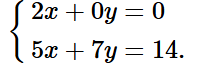

a) Hệ phương trình đã cho không phải là hệ phương trình bậc nhất hai ẩn.

b) Hệ phương trình đã cho có vô số nghiệm.

c) Hệ phương trình đã cho vô nghiệm.

d) Hệ phương trình đã cho có nghiệm duy nhất là (0; 2).

Bài giải chi tiết: 

⦁ Xét phương trình 2x + 0y = 0 và phương trình 5x + 7y = 14: đều là phương trình bậc nhất hai ẩn x và y nên hệ phương trình đã cho là hệ phương trình bậc nhất hai ẩn.

Do đó ý a) đúng.

⦁ Giải hệ phương trình:

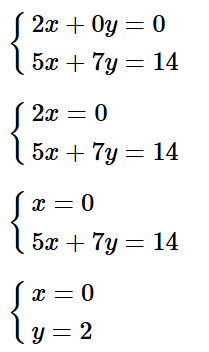
Như vậy, hệ phương trình đã cho có nghiệm duy nhất là (0; 2).

Do đó, ý d) đúng và ý b), c) sai.

Vậy: a) Đúng.

b) Sai.

c) Sai.

d) Đúng.

Bài tập 10 trang 16 sách bài tập Toán 9 Tập 1: Giải các phương trình:

a) (3x + 2)(2x – 5) = 0;

b) (x+2)(−x - )=0;

c) y² – 7y + 2(y – 7) = 0;

d) 4x² – 1 = (2x – 1)(3x + 7).

Bài giải chi tiết: 

a) (3x + 2)(2x – 5) = 0

3x + 2 = 0 hoặc 2x ‒ 5 = 0

x = -  và x =

Vậy phương trình có hai nghiệm là x = -  và x =

b) (x+2)(−x - )=0;

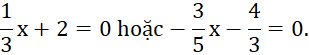
Trường hợp 1:

                           x = ‒6.

⦁ Trường hợp 2: -

                           x =−

Vậy phương trình có hai nghiệm là x = – 6 và  x = −

c) y² – 7y + 2(y – 7) = 0

y(y ‒ 7) + 2(y ‒ 7) = 0

(y – 7)(y + 2) = 0

y ‒ 7 = 0 hoặc y + 2 = 0

y = 7 hoặc y = –2.

Vậy phương trình có hai nghiệm là y = 7 và y = –2.

d) 4x² – 1 = (2x – 1)(3x + 7)

(2x)² – 1² = (2x – 1)(3x + 7)

(2x + 1)(2x – 1) – (2x – 1)(3x + 7) = 0

(2x ‒ 1)(2x + 1 ‒ 3x ‒ 7) = 0

(2x – 1)(– x – 6) = 0

2x ‒ 1 = 0 hoặc ‒ x ‒ 6 = 0

x= hoặc x = –6.

Vậy phương trình có hai nghiệm là x = và x = –6.

Bài tập 11 trang 16 sách bài tập Toán 9 Tập 1: Giải các phương trình:

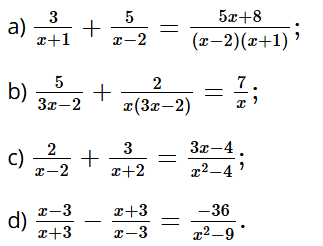
Bài giải chi tiết: 

a) Điều kiện xác định: x + 1 ≠ 0 và x ‒ 2 ≠ 0, hay x ≠ –1 và x ≠ 2.

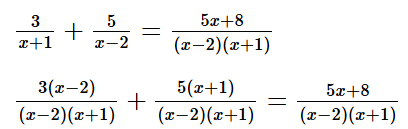
3(x – 2) + 5(x + 1) = 5x + 8

3x ‒ 6 + 5x + 5 = 5x + 8

3x = 9

x = 3 (thoả mãn điều kiện).

Vậy nghiệm của phương trình là x = 3.

b) Điều kiện xác định: x ≠ 0 và 3x ‒ 2 ≠ 0, hay x ≠ 0 và x ≠

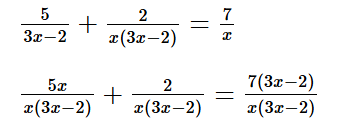
5x + 2 = 7(3x – 2)

5x + 2 = 21x – 14

–16x = –16

x = 1 (thoả mãn điều kiện).

Vậy nghiệm của phương trình là x = 1.

c) Ta có: x² ‒ 4 = (x ‒ 2)(x + 2).

Điều kiện xác định: x ‒ 2 ≠ 0 và x + 2 ≠ 0 hay x ≠ 2 và x ≠ –2.

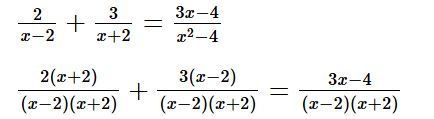
2(x + 2) + 3(x – 2) = 3x – 4

2x + 4 + 3x ‒ 6 = 3x ‒ 4

2x = –2

x = –1 (thoả mãn điều kiện).

Vậy nghiệm của phương trình là x = –1.

d) Ta có: x² ‒ 9 = (x ‒ 3)(x + 3).

Điều kiện xác định: x + 3 ≠ 0 và x ‒ 3 ≠ 0, hay x ≠ –3 và x ≠ 3.

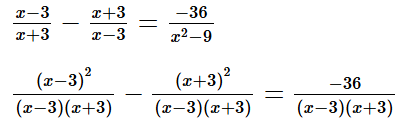
(x – 3)² – (x + 3)² = –36

x² ‒ 6x + 9 ‒ (x² + 6x + 9) = ‒36

‒12x = ‒36

x = 3 (không thoả mãn điều kiện).

Vậy phương trình vô nghiệm.

Bài tập 12 trang 16 sách bài tập Toán 9 Tập 1: Giải các hệ phương trình:

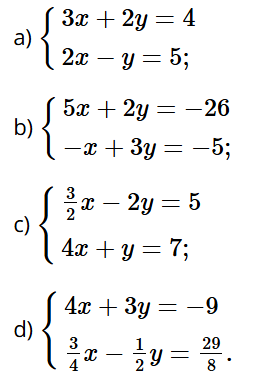
Bài giải chi tiết: 

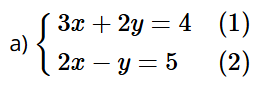
Nhân hai vế của phương trình (2) với 2, ta được: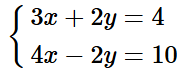

Cộng từng vế hai phương trình của hệ, ta được:

7x = 14, suy ra x = 2.

Thay x = 2 vào phương trình (2), ta được:

2.2 – y = 5, hay 4 – y = 5, do đó y = –1.

Vậy hệ phương trình đã cho có nghiệm duy nhất là (2; ‒1).

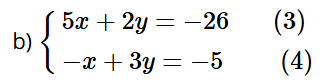
Nhân hai vế của phương trình (4) với 5, ta được:

Cộng từng vế hai phương trình của hệ, ta được:

17y = –51, suy ra y = –3.

Thay y = –3 vào phương trình (4), ta được:

–x + 3.(–3) = –5, hay –x – 9 = –5, do đó x = –4.

Vậy hệ phương trình đã cho có nghiệm duy nhất là (‒4; ‒3).

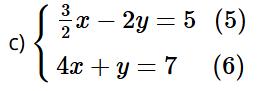
Nhân hai vế của phương trình (6) với 2, ta được: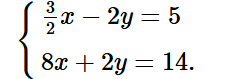

Cộng từng vế hai phương trình của hệ, ta được:

 x = 19 , suy ra x = 2.

Thay x = 2 vào phương trình (6), ta được:

4.2 + y = 7, hay 8 + y = 7, do đó y = –1.

Vậy hệ phương trình đã cho có nghiệm duy nhất là (2; ‒1).

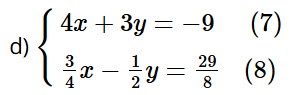
Nhân hai vế của phương trình (8) với 6, ta được: 

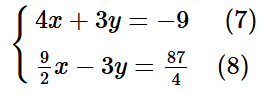
Cộng từng vế hai phương trình của hệ, ta được:

Bài tập 13 trang 17 sách bài tập Toán 9 Tập 1: Giải các hệ phương trình:

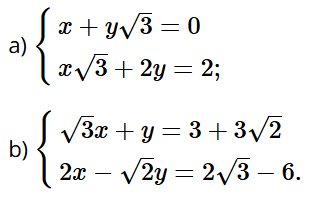
Bài giải chi tiết: 

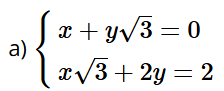
Bài tập 14 trang 17 sách bài tập Toán 9 Tập 1: Một người mua 36 bông hoa hồng và hoa cẩm chướng hết tất cả 174 000 đồng. Giá mỗi bông hoa hồng là 5 500 đồng, giá mỗi bông hoa cẩm chướng là 4 000 đồng. Hỏi người đó đã mua bao nhiêu bông hoa mỗi loại?

Bài giải chi tiết: 

Gọi x (bông) và y (bông) lần lượt là số bông hoa hồng và số bông hoa cẩm chướng người đó mua (x ∈ ℕ*, y ∈ ℕ*).

Do người đó mua 36 bông hoa hồng và hoa cẩm chướng nên ta có phương trình:

x + y = 36. (1)

Số tiền mua hoa hồng là: 5 500x (đồng).

Số tiền mua hoa cẩm chướng là: 4 000y (đồng).

Do mua hết tất cả 174 000 đồng nên ta có phương trình:

5 500x + 4 000y = 174 000 hay 11x + 8y = 348. (2)

Từ (1) và (2) ta có hệ phương trình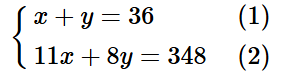

Nhân hai vế của phương trình (1) với 8, ta được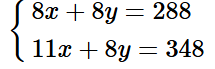

Trừ từng vế của phương trình thứ hai và phương trình thứ nhất, ta được:

3x = 60, suy ra x = 20.

Thay x = 20 vào phương trình (1), ta được:

20 + y = 36, do đó y = 16.

Ta thấy x = 20, y = 16 thoả mãn điều kiện.

Vậy người đó đã mua 20 bông hoa hồng và 16 bông hoa cẩm chướng.

Bài tập 15 trang 17 sách bài tập Toán 9 Tập 1: Một xe tải dự định di chuyển từ A đến B với tốc độ không đổi trong một thời gian nhất định. Nếu tốc độ của xe giảm 10 km/h thì đến B chậm hơn dự định 45 phút. Nếu tốc độ của xe nhanh hơn tốc độ dự định 10 km/h thì sẽ đến B sớm hơn dự định 30 phút. Tính tốc độ và thời gian dự định của xe tải đó.

Bài giải chi tiết: 

Đổi 45 phút = 0,75 giờ; 30 phút = 0,5 giờ.

Gọi x (km/h) là tốc độ dự định, y (giờ) là thời gian dự định của xe tải đó (x > 10; y > 0,5).

Chiều dài quãng đường là: xy (km).

Nếu tốc độ của xe giảm 10 km/h thì đến B chậm hơn dự định 45 phút thì vận tốc xe khi đó là x ‒ 10 (km/h) và thời gian đi là: y + 0,75 (giờ).

Lúc này, chiều dài quãng đường là (x – 10)(y + 0,75) (km).

Ta có phương trình: (x – 10)(y + 0,75) = xy

xy + 0,75x – 10y – 7,5 = xy

0,75x – 10y = 7,5. (1)

Nếu tốc độ của xe nhanh hơn tốc độ dự định 10 km/h thì sẽ đến B sớm hơn dự định 30 phút thì vận tốc xe khi đó là x + 10 (km/h) và thời gian đi là y – 0,5 (giờ).

Lúc này, chiều dài quãng đường là (x + 10)(y – 0,5) (km).

Ta có phương trình: (x + 10)(y – 0,5) = xy

xy – 0,5x + 10y – 5 = xy

0,5x – 10y = –5. (2)

Từ (1) và (2), ta có hệ phương trình: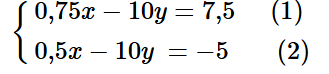

Trừ từng vế hai phương trình (1) và phương trình (2) của hệ, ta được:

0,25x = 12,5, suy ra x = 50.

Thay x = 50 vào phương trình (2), ta được:

0,5 . 50 – 10y = –5, hay 25 – 10y = –5, do đó y = 3.

Ta thấy x = 50 và y = 3 thoả mãn điều kiện.

Vậy tốc độ dự định của x là 50 km/h, thời gian dự định di chuyển từ A đến B là 3 giờ.

Bài tập 16 trang 17 sách bài tập Toán 9 Tập 1: Một gia đình có bốn người lớn và ba trẻ em mua vé xem xiếc hết 370 000 đồng. Một gia đình khác có hai người lớn và hai trẻ em cũng mua vé xem xiếc tại rạp đó hết 200 000 đồng. Hỏi giá bán của mỗi loại vé cho người lớn và trẻ em là bao nhiêu? Biết rằng rạp đó bán hai hạng vé: người lớn và trẻ em, mỗi người vào xem phải mua một vé đúng hạng.

Bài giải chi tiết: 

Gọi x (đồng) là giá một vé người lớn, y (đồng) là giá một vé trẻ em (x > 0, y > 0).

Số tiền trả cho 4 vé người lớn là: 4x (đồng).

Số tiền trả cho 3 vé trẻ em là: 3y (đồng).

Một gia đình có bốn người lớn và ba trẻ em mua vé xem xiếc hết 370 000 đồng nên ta có phương trình: 4x + 3y = 370 000. (1)

Số tiền trả cho 2 vé người lớn là: 2x (đồng).

Số tiền trả cho 2 vé trẻ em là: 2y (đồng).

Một gia đình khác có hai người lớn và hai trẻ em cũng mua vé xem xiếc tại rạp đó hết 200000 đồng nên ta có phương trình 2x + 2y = 200 000. (2)

Từ (1) và (2) ta có hệ phương trình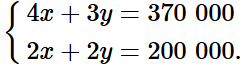

Nhân hai vế của phương trình (2) với ‒2, ta được: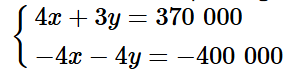

Cộng từng vế hai phương trình của hệ, ta có:

‒y = ‒30 000, do đó y = 30 000.

Thay y = 30 000 vào phương trình (1), ta được:

4x + 3.30 000 = 370 000, hay 4x + 90 000 = 370 000, do đó x = 70 000.

Ta thấy x = 70 000, y = 30 000 thoả mãn điều kiện.

Vậy giá một vé người lớn là 70 000 đồng, giá một vé trẻ em là 30 000 đồng.

Bài tập 17 trang 17 sách bài tập Toán 9 Tập 1: Một trường tuyển được 85 học sinh vào hai lớp năng khiếu bóng rổ và bóng chuyền. Nếu chuyển 25 học sinh từ lớp bóng rổ sang lớp bóng chuyền thì số học sinh của lớp bóng chuyền bằng số học sinh của lớp bóng rổ. Hãy tính xem mỗi lớp có bao nhiêu học sinh.

Bài giải chi tiết: 

Gọi x, y lần lượt là số học sinh của lớp bóng rổ và lớp bóng chuyền (x ∈ ℕ*, y ∈ ℕ*, x < 85, y < 85).

Do trường có 85 học sinh nên ta có: x + y = 85. (1)

Số học sinh lớp bóng chuyền sau khi chuyển 25 học sinh từ lớp bóng rổ sang là: y + 25 (học sinh).

Lúc này, số học sinh lớp bóng rổ còn lại là: x ‒ 25 (học sinh).

Theo bài, sau khi chuyển 25 học sinh từ lớp bóng rổ sang lớp bóng chuyền thì số học sinh của lớp bóng chuyền bằng số học sinh của lớp bóng rổ nên ta có phương trình:

y+25 = (x−25)

5(y + 25) = 12(x – 25)

5y + 125 = 12x – 300

12x – 5y = 425. (2)

Từ (1) và (2) ta có hệ phương trình: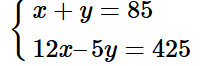

Nhân hai vế phương trình (1) với 5, ta được: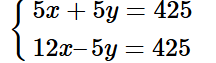

Cộng từng vế hai phương trình của hệ, ta được:

17x = 850, suy ra x = 50.

Thay x = 50 vào phương trình (1), ta được:

50 + y = 85, do đó y = 35.

Ta thấy x = 50, y = 35 thoả mãn điều kiện.

Vậy lớp bóng rổ có 50 học sinh và lớp bóng chuyền có 35 học sinh.

Bài tập 18 trang 17 sách bài tập Toán 9 Tập 1: Hai khối hợp kim có tỉ lệ đồng và kẽm khác nhau: Khối thứ nhất có tỉ lệ đồng và kẽm là 8 : 2 và khối thứ hai có tỉ lệ đồng và kẽm là 3 : 7, được đưa vào lò để luyện ra khối hợp kim có khối lượng 250 kg và có tỉ lệ đồng và kẽm là 5 : 5. Tính khối lượng mỗi khối hợp kim. (Biết rằng, khối lượng hao hụt và khối lượng các tạp chất không đáng kể.)

Bài giải chi tiết: 

Gọi x (kg) và y (kg) lần lượt là khối lượng khối hợp kim thứ nhất và khối hợp kim thứ hai (0 < x < 250, 0 < y < 250).

Do khối hợp kim có khối lượng 250 kg nên ta có x + y = 250. (1)

Do khối thứ nhất có tỉ lệ đồng và kẽm là 8 : 2 nên khối lượng đồng chiếm khối lượng khối hợp kim thứ nhất.

Như vậy, khối lượng đồng trong khối kim loại thứ nhất là:

Do khối thứ hai có tỉ lệ đồng và kẽm là 3 : 7 nên khối lượng đồng chiếm khối lượng khối hợp kim thứ hai.

Như vậy, khối lượng đồng trong khối kim loại thứ hai là:

Do trong khối hợp kim mới có tỉ lệ đồng và kẽm là 5 : 5 nên khối lượng đồng chiếm
Như vậy, khối lượng đồng trong khối hợp kim mới là: =125 (kg)

Khi đó, ta có phương trình: 

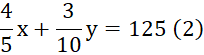
Từ (1) và (2) ta có hệ phương trình: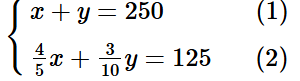
Nhân hai vế của phương trình (1) với 3 và nhân hai vế của phương trình (2) với 10, ta được: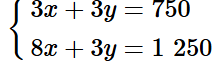

Trừ từng vế phương trình thứ hai và phương trình thứ nhất, ta được:

5x = 500, suy ra x = 100.

Thay x = 100 vào phương trình (1), ta được:

100 + y = 250, do đó y = 150.

Ta thấy x = 100, y = 150 thoả mãn điều kiện.

Vậy khối hợp kim thứ nhất có khối lượng 100 kg và khối hợp kim thứ hai có khối lượng 150 kg.