CHƯƠNG 7

BÀI TẬP CUỐI CHƯƠNG 7

TRẮC NGHIỆM :

Bài tập 1 (trang 46):

Một công ty chuyển phát nhanh thống kê thời gian từ lúc nhận đến lúc giao của 120 đơn hàng trong khu vực nội thành Thành phố Hồ Chí Minh ở biểu đồ sau (đơn vị: phát).

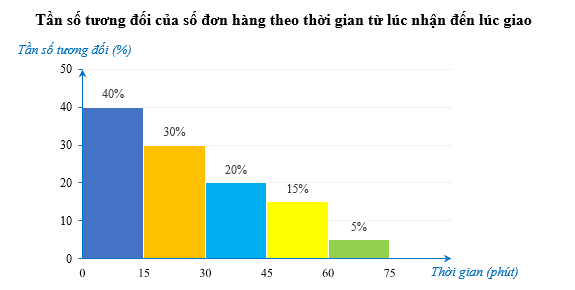
a) Tần số tương đối của các đơn hàng có thời gian từ lúc nhận đến lúc giao dưới 30 phút là

A. 30%.

B. 40%.

C. 60%.

D. 70%.

b) Thời gian từ lúc nhận đến lúc giao hàng phổ biến nhất là khoảng

A. [0; 15).

B. [15; 30).

C. [30; 45).

D. [45; 60).

c) Tần số của các đơn hàng có thời gian từ lúc nhận đến lúc giao từ 60 phút trở lên là

A. 5.

B. 6.

C. 7.

D. 15.

d) Đúng 15% số đơn hàng có thời gian từ lúc nhận đến lúc giao

A. dưới 15 phút.

B. trên 45 phút.

C. từ 15 đến 30 phút.

D. từ 30 đến 60 phút.

Bài giải chi tiết: 

a) Đáp án đúng là: D

Tần số tương đối của các đơn hàng có thời gian từ lúc nhận đến lúc giao dưới 30 phút là: 40% + 30% = 70%.

b) Đáp án đúng là: A

Thời gian từ lúc nhận đến lúc giao hàng phổ biến nhất là khoảng [0; 15).

c) Đáp án đúng là: B

Tần số của các đơn hàng có thời gian từ lúc nhận đến lúc giao từ 60 phút trở lên là:

120 . 5% = 6.

d) Đáp án đúng là: B

Đúng 15% số đơn hàng có thời gian từ lúc nhận đến lúc giao từ 30 đến 45 phút hoặc trên 45 phút.

Do đó ta chọn phương án B.

Bài tập 2 (trang 47):

Chị Hằng thống kê lại thời gian chạy cự li 800 m của mình ở một số lần luyện tập trong năm 2016 và 2017 như sau:

a) Tần số tương đối của các lần chị Hằng chạy hết ít hơn 124 giây trong mẫu số liệu năm 2016 là

A. 35%.

B. 46%.

C. 60%.

D. 65%.

b) Tần số tương đối của các lần chị Hằng chạy hết nhiều hơn 125 giây trong mẫu số liệu năm 2017 là

A. 0%.

B. 8%.

C. 10%.

D. 17,5%.

c) So với số liệu năm 2016, trong số liệu năm 2017, tần số tương đối của các lần chị Hằng chạy hết ít hơn 123 giây tăng thêm

A. 155%.

B. 17%.

C. 19%.

D. 28,5%.

d) Một lần chạy được gọi là đạt thành tích thấp nếu thời gian chạy không đạt dưới 124 giây. So với số liệu năm 2016, trong số liệu năm 2017, tần số tương đối của các lần chị Hằng đạt thành tích thấp giảm

A. 27%.

B. 22,8%.

C. 28,6%.

D. 11%.

Bài giải chi tiết: 

Tổng số lần chị Hằng chạy năm 2016 là: 11 + 15 + 7 + 5 + 2 = 40.

Tổng số lần chị Hằng chạy năm 2017 là: 28 + 18 + 4 + 0 + 0 = 50.

a) Đáp án đúng là: D

Tần số chị Hằng chạy hết ít hơn 124 giây trong mẫu số liệu năm 2016 là: 11 + 15 = 26.

Tần số tương đối của các lần chị Hằng chạy hết ít hơn 124 giây trong mẫu số liệu năm 2016 là  . 100% = 65 % 
b) Đáp án đúng là: A

Tần số chị Hằng chạy hết nhiều hơn 125 giây trong mẫu số liệu năm 2017 là: 0 + 0 = 0.

Tần số tương đối của các lần chị Hằng chạy hết nhiều hơn 125 giây trong mẫu số liệu năm 2017 là:  . 100% = 0 %

c) Đáp án đúng là: D

⦁ Tần số chị Hằng chạy ít hơn 123 giây trong mẫu số liệu năm 2016 là: 11.

Tần số tương đối của các lần chị Hằng chạy hết ít hơn 123 giây trong mẫu số liệu năm 2016 là:  . 100% = 27,5 %

⦁ Tần số chị Hằng chạy ít hơn 123 giây trong mẫu số liệu năm 2017 là: 28.

Tần số tương đối của các lần chị Hằng chạy hết ít hơn 123 giây trong mẫu số liệu năm 2017 là:   . 100% = 56 %

Như vậy, so với số liệu năm 2016, trong số liệu năm 2017, tần số tương đối của các lần chị Hằng chạy hết ít hơn 123 giây tăng thêm 56% – 27,5% = 28,5%.

d) Đáp án đúng là: A

⦁ Tần số chị Hằng chạy đạt thành tích thấp (thời gian chạy không đạt dưới 124 giây) giây trong mẫu số liệu năm 2016 là: 7 + 5 + 2 = 14.

Tần số tương đối của các lần chị Hằng chạy đạt thành tích thấp (thời gian chạy không đạt dưới 124 giây) giây trong mẫu số liệu năm 2016 là: 35%.

⦁ Tần số chị Hằng chạy đạt thành tích thấp (thời gian chạy không đạt dưới 124 giây) giây trong mẫu số liệu năm 2017 là: 4 + 0 + 0 = 4.

Tần số tương đối của các lần chị Hằng chạy đạt thành tích thấp (thời gian chạy không đạt dưới 124 giây) giây trong mẫu số liệu năm 2017 là: 8%.

Như vậy, so với số liệu năm 2016, trong số liệu năm 2017, tần số tương đối của các lần chị Hằng đạt thành tích thấp giảm 35% – 8% = 27%.

Bài tập 3 (trang 48):

Chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Một công ty mua các tấm gốm nhỏ để sản xuất thiết bị điện tử. Các tấm gốm được kiểm tra bằng mắt trước khi đưa vào sản xuất. Tấm gốm bị lỗi sẽ làm ảnh hưởng đến hiệu suất của thiết bị. Số liệu sau đây thể hiện số lỗi tìm thấy trên 30 tấm gốm được lựa chọn ngẫu nhiên.

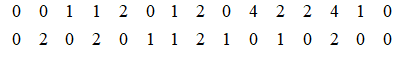
a) Số lỗi trên 30 tấm gốm trên nhận 4 giá trị khác nhau.

b) Tần số của tấm gốm có trên 3 lỗi là 2.

c) Có trên 50% các tấm gốm không bị lỗi.

d) Giá trị 8 có tần số là 2.

Bài giải chi tiết: 

Trong các số liệu đã cho, có 4 giá trị khác nhau là: 0; 1; 2; 4. Do đó ý a) là đúng.

Tần số của tấm gốm có 0; 1; 2; 4 lỗi lần lượt là: 12; 8; 8; 2.

Do đó tần số của tấm gốm có trên 3 lỗi (hay trong trường hợp này chính là tần số của tấm gốm có 4 lỗi) là: 2. Nên ý b) là đúng.

Tần số tương đối của các tấm gốm không bị lỗi là: . 100% = 40 %. Do đó ý c) là sai.

Trong các số liệu đã cho, không có giá trị 8. Do đó ý d) là sai.

Vậy:

a) Đ;

b) Đ;

c) S;

d) S.

Bài tập 4 (trang 48):

Chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Bảng sau ghi lại nhiệt độ lúc 12 giờ hằng ngày tại một trạm quan trắc vào tháng 11/2023.

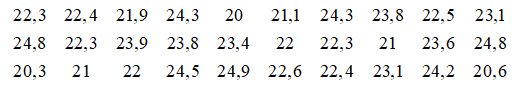
Chia dữ liệu trên thành các nhóm có độ dài bằng nhau với nhóm thứ nhất là [20; 21).

a) Số nhóm dữ liệu là 6.

b) Độ rộng của các nhóm dữ liệu đều bằng 1.

c) Tần số của nhóm [20; 21) là 3.

d) Nhóm có tần số tương đối cao nhất là nhóm [23; 24).

Bài giải chi tiết: 

⦁ Độ rộng của nhóm [20; 21) là: 21 – 20 = 1. Do đó ý b) là đúng.

⦁ Các nhóm dữ liệu là: [20; 21); [21; 22); [22; 23); [23; 24); [24; 25). Có 5 nhóm dữ liệu. Do đó ý a) là sai.

⦁ Các giá trị của nhóm dữ liệu [20; 21) là: 20; 23,3; 20,6. Do đó tần số của nhóm [20; 21) là 3. Do đó ý c) là sai.

⦁ Tần số của các nhóm [20; 21); [21; 22); [22; 23); [23; 24); [24; 25) lần lượt là: 3; 4; 9; 7; 7. Nhóm có tần số cao nhất là nhóm [22; 23). Do đó ý d) là sai.

Vậy:

a) S;

b) Đ;

c) Đ;

d) S.

BÀI TẬP TỰ LUẬN: 

Bài tập 5 (trang 48):

Cô Lan ghi lại số cuộc gọi điện thoại cô thực hiện mỗi ngày trong tháng 9/2023 ở bảng sau:

a) Trong bảng số liệu trên, có bao nhiêu giá trị khác nhau? Tìm tần số của các giá trị đó.

b) Lập bảng tần số cho mẫu số liệu trên.

c) Vẽ biểu đồ cột biểu diễn số liệu ở bảng tần số trên.

Bài giải chi tiết: 

a) Trong các số liệu trên, có 6 giá trị khác nhau là: 0; 1; 2; 3; 4; 5.

Tần số của các giá trị 0; 1; 2; 3; 4; 5 lần lượt là: 2; 6; 6; 9; 3; 4.

b) Bảng tần số:

c) Biểu đồ cột:

Bài tập 6 (trang 49):

Bảng sau ghi lại số bàn thắng mà câu lạc bộ bóng đá ABC đã ghi được trong mỗi trận đấu sau một mùa giải.

a) Trong mùa giải nói trên, câu lạc bộ ABC đã thi đấu bao nhiêu trận?

b) Số bàn thắng câu lạc bộ ABC ghi được trong mỗi trận đấu nhận những giá trị nào? Xác định tần số của mỗi giá trị đó.

c) Lập bảng tần số tương đối và vẽ biểu đồ hình quạt biểu diễn mẫu số liệu trên (kết quả làm tròn đến hàng phần mười).

Bài giải chi tiết: 

a) Trong mùa giải nói trên, câu lạc bộ ABC đã thi đấu 26 trận.

b) Số bàn thắng câu lạc bộ ABC ghi được trong mỗi trận đấu nhận các giá trị: 0; 1; 2; 3; 4. Tần số của các giá trị này lần lượt là: 6; 9; 7; 3; 1.

c) Gọi f₁, f₂, f₃, f₄, f₅ lần lượt là tần số tương đối của các giá trị: 0; 1; 2; 3; 4.

Ta có: 

f₁ = . 100% ≈ 23,1%

f₂ = . 100% ≈ 34,6%

f₃ = . 100% ≈ 26,9%

f₄ = . 100% ≈ 11,5 %

f₅ ≈ 100% - 23,1% - 34,6% - 26,9% - 11,5% ≈ 3,9%

Bảng tần số tương đối:

Số đo cung tròn tương ứng với các hình quạt tròn biểu diễn tần số tương đối của các giá trị như sau:

Biểu đồ tần số tương đối hình quạt tròn:

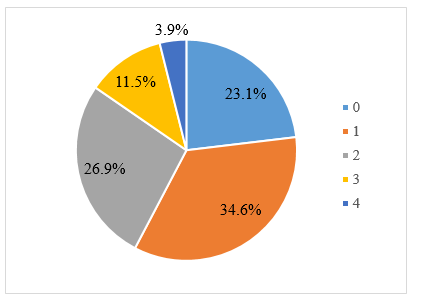
Bài tập 7 (trang 49):

Người ta nghiên cứu về độ bền của hai loại ti vi màn hình phẳng 43 inch của hai hãng sản xuất A và B. Thời gian sử dụng của một số chiếc ti vi từ khi mua về đến khi gặp sự cố hỏng hóc đầu tiên được ghi lại ở bảng tần số sau:

a) Hãy tính tần số tương đối của ti vi mỗi hãng theo thời gian sử dụng.

b) Một chiếc ti vi được gọi là bền nếu nó có thời gian sử dụng từ 6 năm trở lên. Hãy so sánh tần số tương đối của ti vi bền của hai hãng A và B.

Bài giải chi tiết: 

a) * Ti vi hãng A:

Cỡ mẫu N = 6 + 39 + 54 + 30 + 21 = 150.

Tần số của các nhóm [3; 4); [4; 5); [5; 6); [6; 7); [7; 8) lần lượt là m₁ = 6; m₂ = 39; m₃ = 54; m₄ = 30; m₅ = 21.

Gọi f₁, f₂, f₃, f₄, f₅ lần lượt là tần số tương đối của các nhóm [3; 4); [4; 5); [5; 6); [6; 7); [7; 8).

Ta có: 

f₁ = . 100% = 4 %

f₂ = . 100% = 26%

f₃ = . 100% = 36 %

f₄ = . 100% = 20 %

f₅ = . 100% = 14 %

* Ti vi hãng B:

Cỡ mẫu N = 15 + 75 + 90 + 40 + 30 = 250.

Tần số của các nhóm [3; 4); [4; 5); [5; 6); [6; 7); [7; 8) lần lượt là m’₁ = 15; m’₂ = 75; m’₃ = 90; m’₄ = 40; m’₅ = 30.

Gọi f’₁, f’₂, f’₃, f’₄, f’₅ lần lượt là tần số tương đối của các nhóm [3; 4); [4; 5); [5; 6); [6; 7); [7; 8).

Ta có: 

f’₁ = . 100% = 6 %

f’₂ = . 100% = 30 %

f’₃ = . 100% = 36 %

f’₄ = . 100% = 16 %

f’₅ = . 100% = 12 %

Vậy bảng tần số tương đối của ti vi mỗi hãng theo thời gian sử dụng như sau:

b) Tần số tương đối của ti vi bền (có thời gian sử dụng từ 6 năm trở lên) của hãng A là 20% + 14% = 34%.

Tần số tương đối của ti vi bền (có thời gian sử dụng từ 6 năm trở lên) của hãng B là 16% + 12% = 28%.

Ta thấy 34% > 28% nên tần số tương đối của ti vi bền do hãng A sản xuất cao hơn hãng B.

Bài tập 8 (trang 49):

Vào đầu năm học, người ta lựa chọn ngẫu nhiên một số học sinh lớp 9 ở khu vực A và khu vực B để kiểm tra tình trạng cân nặng. Kết quả khảo sát được ghi lại ở bảng sau:

a) Hãy tính tần số tương đối của học sinh ở mỗi khu vực theo tình trạng cân nặng.

b) Hãy lựa chọn, vẽ biểu đồ phù hợp và so sánh tình trạng cân nặng của học sinh ở hai khu vực.

Bài giải chi tiết: 

a) * Khu vực A:

Cỡ mẫu N = 16 + 40 + 16 + 8 = 80.

Tần số của các nhóm thiếu cân, bình thường, thừa cân, béo phì lần lượt là m₁ = 16; m₂ = 40; m₃ = 16; m₄ = 8.

Gọi f₁, f₂, f₃, f₄, f₅ lần lượt là tần số tương đối của các nhóm thiếu cân, bình thường, thừa cân, béo phì.

Ta có: 

f₁ = . 100% = 20 %

f₂ = . 100% = 50 %

f₃ = . 100% = 20 %

f₄ = . 100% = 10 %

* Khu vực B:

Cỡ mẫu N = 6 + 34 + 5 + 5 = 50.

Tần số của các nhóm thiếu cân, bình thường, thừa cân, béo phì lần lượt là m’₁ = 6; m’₂ = 34; m’₃ = 5; m’₄ = 5.

Gọi f’₁, f’₂, f’₃, f’₄, f’₅ lần lượt là tần số tương đối của các nhóm thiếu cân, bình thường, thừa cân, béo phì.

f’₁ = . 100% = 12 %

f’₂ = . 100% = 68 %

f’₃ = . 100% = 10 %

f’₄ = . 100% = 10 %

Vậy bảng tần số tương đối của học sinh ở mỗi khu vực theo tình trạng cân nặng:

b) Để so sánh tình trạng cân nặng của học sinh ở hai khu vực, ta sử dụng biểu đồ tần số tương đối dạng cột kép.

Biểu đồ cột kép để so sánh tình trạng cân nặng của học sinh ở hai khu vực như sau:

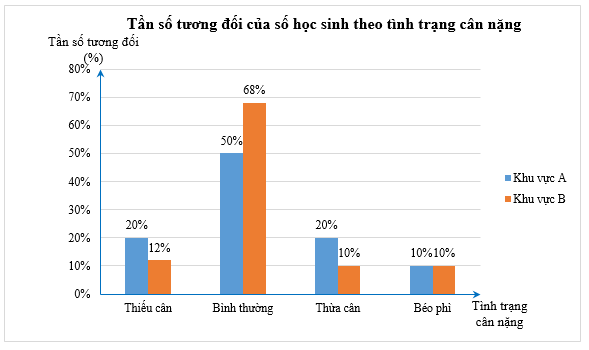
Từ biểu đồ, ta thấy:

⦁ Tần số tương đối của học sinh thiếu cân và thừa cân ở khu vực A cao hơn khu vực B.

⦁ Tần số tương đối của số học sinh có cân nặng bình thường ở khu vực A thấp hơn khu vực B.

⦁ Tần số tương đối của số học sinh béo phì ở hai khu vực là như nhau.

Bài tập 9 (trang 49):

Trong bảng số liệu sau có một số liệu không chính xác. Hãy tìm số liệu đó và sửa lại cho đúng.

Bài giải chi tiết: 

Tổng các tần số tương đối là 15% + 25% + 35% + 25% = 100%, nên nếu có số liệu về tần số tương đối sai thì phải có ít nhất hai số liệu sai.

Mà chỉ có một số liệu sai trong bảng nên các giá trị tần số tương đối đều chính xác.

Ta có ≠ = do đó số liệu tần số 10 là sai. 

Theo tính chất tỉ lệ thức, ta có giá trị đúng là

Vậy bảng số liệu đúng như sau: