CHƯƠNG 6

BÀI TẬP CUỐI CHƯƠNG 6

TRẮC NGHIỆM:

Bài tập 1 (trang 16):

Điểm nào sau đây thuộc đồ thị của hàm số y = -  x² 
A. (3; 8).

B. (–3; 6).

C. (–3; –6).

D. (3; –8).

Bài giải chi tiết: 

Đáp án đúng là C 

Thay x = 3 vào hàm số y = -  x² , ta được : -   . 3²= -6 

Do đó điểm (3; 8) và (3; –8) không thuộc đồ thị hàm số y = -  x²

Thay x = ‒3 vào hàm số y = -  x²

Ta được -   . (-3)² = -6

Do đó điểm (–3; 6) không thuộc đồ thị hàm số y = -  x² , điểm (–3; –6) thuộc đồ thị hàm số.

Bài tập 2 (trang 16):

Cho hàm số y = x². Khi y = 4 thì

A. x = –2.

B. x = –2 hoặc x = 2.

C. x = –4 hoặc x = 4.

D. x = 2.

Bài giải chi tiết: 

Đáp án đúng là: B

Khi y = 4, thay vào hàm số y = x², ta được:

x² = 4, suy ra x = 2 hoặc x = ‒2.

Bài tập 3 (trang 16):

Đồ thị của hàm số y = ax² (a ≠ 0) đi qua điểm A(1; – 2). Giá trị của a bằng

A. 2.

B. –2.

C.

D. -

Bài giải chi tiết: 

Đáp án đúng là: B

Do đồ thị của hàm số y = ax² (a ≠ 0) đi qua điểm A(1; – 2) nên thay x = 1 và y = ‒2 vào hàm số y = ax², ta được

a.1² = ‒2 hay a = ‒2.

Bài tập 4 (trang 16):

Cho phương trình ax² + bx + c = 0 (a ≠ 0) có ∆ = b² – 4ac = 0. Khi đó, phương trình có hai nghiệm là

A.  =  = -

B.  =  = - 
C.  =  =    

D.  =  =

Bài giải chi tiết: 

Đáp án đúng là: A

Phương trình đã cho có ∆ = 0 nên nó có nghiệm kép  =  = -

Bài tập 5 (trang 16):

Nghiệm của phương trình x² – 15x – 16 = 0 là :

A.  =  = 16

B.  =  = - 16
C.  =  = - 16

D.  =  = 16

Bài giải chi tiết: 

Đáp án đúng là: A

Phương trình x² – 15x – 16 = 0 có a ‒ b + c = 1 ‒ (‒15) ‒16 = 1 + 15 ‒16 = 0.

Do đó, phương trình có hai nghiệm là  =  = 16

Bài tập 6 (trang 16):

Phương trình nào dưới đây không là phương trình bậc hai một ẩn?

A.

B. 
C.

D.

Bài giải chi tiết: 

Đáp án đúng là: D

Phương trình là phương trình bậc nhất một ẩn, không phải phương trình bậc hai một ẩn.

Bài tập 7 (trang 16):

Gọi S và P lần lượt là tổng và tích hai nghiệm của phương trình x² + 3x – 70 = 0. Khi đó, giá trị của S và P là

A. S = 3; P = 70.

B. S = –3; P = 70.

C. S = –3; P = –70.

D. S = 3; P = –70.

Bài giải chi tiết: 

Xét phương trình x² + 3x – 70 = 0.

Ta có: ∆ = 3² – 4.1.(–70) = 9 + 280 = 289 > 0.

Do đó phương trình đã cho có hai nghiệm phân biệt.

Theo định lí Viète, ta có:

S =  + =

P = -70 

Bài tập 8 (trang 16):

ho phương trình x² + 6x – 91 = 0. Gọi x₁, x₂ là hai nghiệm của phương trình. Khi đó, giá trị của biểu thức ² + ²  - 2  - 2là 

A. 127.

B. 230.

C. –230.

D. –127.

Bài giải chi tiết: 

Đáp án đúng là: B

Xét phương trình x² + 6x – 91 = 0.

Ta có: ∆’ = 3² – 1.1(–91) = 9 + 91 = 100 > 0.

Do đó phương trình đã cho có hai nghiệm phân biệt.

Theo định lí Viète, ta có:  + = -91 

Thay x₁ + x₂ = ‒ 6 và x₁x₂ = ‒91 vào biểu thức trên, ta được:

(‒6)² ‒ 2.(‒91) ‒ 2.(‒6) = 36 + 182 + 12 = 230.

Bài tập 9 (trang 17):

Cho hàm số y = ax² (a ≠ 0).

a) Giá trị a để đồ thị của hàm số đi qua điểm (2; 2) là a = 2.

b) Nếu a > 0 thì đồ thị của hàm số nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.

c) Nếu a < 0 thì đồ thị của hàm số nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.

d) Đồ thị của hàm số là một đường cong parabol đỉnh O, nhận trục tung làm trục đối xứng.

Bài giải chi tiết: 

Thay x = 2, y = 2 vào hàm số y = ax², ta được:

2 = 2².a hay 4a = 2, suy ra a =

Do đó ý a) là sai.

Nếu a > 0 thì đồ thị của hàm số y = ax² (a ≠ 0) nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị. Do đó ý b) là đúng.

Nếu a < 0 thì đồ thị của hàm số y = ax² (a ≠ 0) nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị. Do đó ý c) là đúng.

Đồ thị của hàm số y = ax² (a ≠ 0) là một đường cong parabol đỉnh O, nhận trục tung làm trục đối xứng. Do đó ý d) là đúng.

Vậy:

a) S.

b) Ð.

c) Ð.

d) Đ.

Bài tập 10 (trang 17):

Cho phương trình 5x² – 7x + 2 = 0.

a) Phương trình có a – b + c = 0 nên có hai nghiệm là

b) Phương trình có a + b + c = 0 nên có hai nghiệm là

c) Gọi x₁, x₂ là hai nghiệm của phương trình. Khi đó ² + ² =

d) Gọi x₁, x₂ là hai nghiệm của phương trình. Khi đó ² + ² = 
Bài giải chi tiết: 

a) S.

b) Đ.

c) S.

d) Đ.

Bài tập 11 (trang 17):

Cho phương trình ax² + bx + c = 0 (a ≠ 0).

a) Khi ∆ = 0, phương trình có nghiệm kép

b) Khi ∆ = 0, phương trình có nghiệm kép

c) Khi ∆ > 0, phương trình có nghiệm kép

d) Khi b = 2b’, ∆’ = b’ – ac > 0, phương trình có hai nghiệm phân biệt

Bài giải chi tiết: 

Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có ∆ = 0 thì phương trình đó có nghiệm kép . Do đó ý a) là sai, ý b) là đúng.

Vậy:

a) S.

b) Ð.

c) Ð.

d) S.

TỰ LUẬN :

Bài tập 12 (trang 17):

Cho hai hàm số y =  x²  và y =  x²

a) Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ.

b) Nhận xét về tính đối xứng của hai đồ thị qua trục Ox.

c) Xác định m để đường thẳng d: y = (3m – 2)x + 5 cắt parabol (P): y =  x²  tại điểm E có hoành độ bằng -2

Bài giải chi tiết: 

Ta có bảng giá trị của hai hàm số:

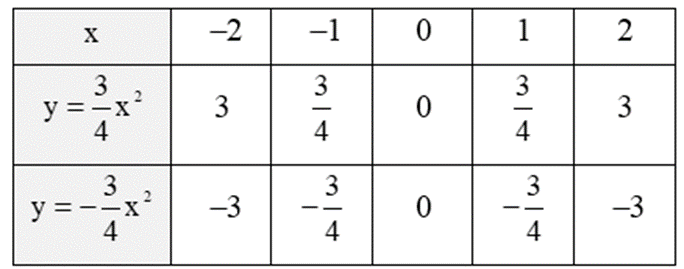
• Trên mặt phẳng Oxy, lấy điểm A(‒2; 3); B (-1; O(0; 0); C(1; D(2;3);

• Đồ thị của hàm số y =  x²  là một đường parabol đỉnh O, đi qua 5 điểm A, B, O, C, D và có dạng như hình vẽ.

Đồ thị của hàm số y =  x² là một đường parabol đỉnh O, đi qua 5 điểm A’, B’, O, C’, D’ và có dạng như hình vẽ.

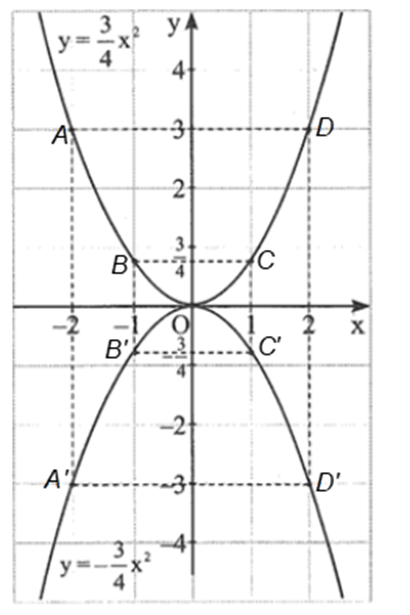
b) Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.

c) Đường thẳng d cắt parabol (P) tại điểm E có hoành độ –2, nên thay x = –2 vào y =  x²   ta được y = e. Do đó ta có điểm E (-2;3) 

Điểm E(–2; 3) thuộc đường thẳng d, nên thay x = –2 và y = 3 vào hàm số y = (3m – 2)x + 5, ta được:

3 = (3m – 2).(–2) + 5

‒6m + 4 + 5 ‒ 3 = 0

‒6m = ‒6

m = 1.

Vậy m = 1.

Bài tập 13 (trang 17):

Trên mặt phẳng toa độ Oxy, cho parabol (P): y = ax² (a ≠ 0) đi qua điểm M(2; –2).

a) Tìm hệ số a, vẽ (P) với a vừa tìm được.

b) Tìm tung độ của điểm thuộc parabol có hoành độ x = –3.

c) Tìm các điểm thuộc parabol có tung độ y = –4,5.

Bài giải chi tiết: 

a) Đồ thị hàm số (P): y = ax² đi qua điểm M(2; –2) nên thay x = 2; y = –2 vào hàm số y = ax², ta được

‒2 = a.2² hay 4a = ‒2, suy ra a =
Vậy (P): y = x²

Ta có bảng giá trị của hàm số:

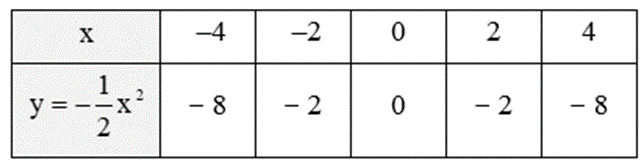
• Trên mặt phẳng tọa độ Oxy, lấy các điểm A(‒4; ‒8); B (‒2; ‒2); O(0; 0); C(2; ‒2); D(4; ‒8).

• Đồ thị của hàm số y = x² là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như hình vẽ.

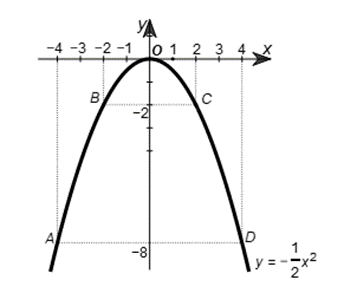
b) Thay x = –3 vào hàm số y =  x², ta được y =

Vậy tung độ của điểm thuộc parabol có hoành độ x = –3 là bằng

c) Thay  y = –4,5 vào hàm số y =  x², ta được: x = 3 hoặc x = -3

Vậy các điểm (–3; –4,5) và (3; –4,5) thuộc parabol có tung độ y = –4,5.

Bài tập 14 (trang 18):

a) Vẽ đồ thị (P) của hàm số y =  x² và đường thẳng d: y =  x+1 trên cùng một mặt phẳng toạ độ Oxy.

b) Tìm tọa độ giao điểm của (P) và d bằng phép tính.

Bài giải chi tiết: 

a) Vẽ hai đồ thị hàm số y = x² và đường thẳng d: y = x+1 ta có:

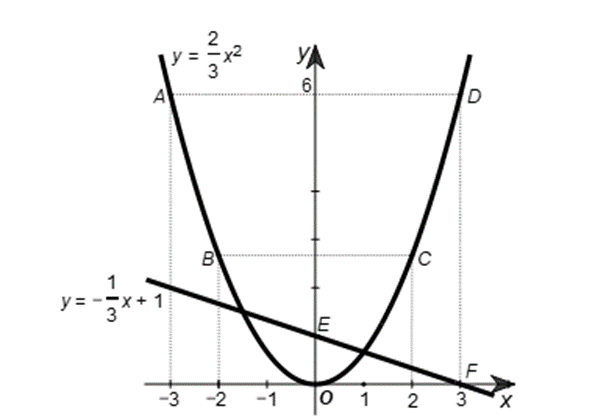
b) Gọi ( là tọa độ giao điểm của (P) và d. 

Khi đó, ta có  =  ² và  =   + 1

Suy ra phương trình : 2 ² + - 3 = 0 

Phương trình trên a + b + c = 2 + 1 ‒ 3 = 0 nên phương trình có hai nghiệm phân biệt là =

Thay  vào hàm số y =  x² ta được  =

Thay = hàm số y =  x² ta được  =

Vậy toạ độ giao điểm của (P) và d là (1 ; (
Bài tập 15 (trang 18):

Giải các phương trình:

a) 7 x²+ 14x = 0

b) 5x² – 3 = 0;

c) 7x² – 5x = 10 – 2x;

d) (x + 7)² = 81.

Bài giải chi tiết: 

a) 7 x²+ 14x = 0

x (7x + 14) = 0

x = 0 hoặc 7x + 14= 0

x = 0 hoặc x = −2.

Vậy phương trình có hai nghiệm x = 0; x = −2.

b) 5x² – 3 = 0

5x² = 3

x² =

x = hoặc x = -

x = hoặc x = -

Vậy phương trình có hai nghiệm là x = ; x = -

c) 7x² – 5x = 10 – 2x

7x² ‒ 3x ‒ 10 = 0

Phương trình trên có a ‒ b + c = 7 ‒ (‒3) + (‒10) = 0.

Vậy phương trình có hai nghiệm là ;

d) (x + 7)² = 81.

x + 7 = 9 hoặc x + 7 = ‒9

x = 2 hoặc x = ‒16

Vậy phương trình có hai nghiệm là x = 2; x = ‒16.

Bài tập 16 (trang 18):

Giải các phương trình:

a) 3x² + 23x – 36 = 0;

b) x² + x = 1

c) 7x² – 2x + 1 = 0

d) x(2x + 5) = x² – 9.

Bài giải chi tiết: 

a) Xét phương trình 3x² + 23x – 36 = 0

Ta có: a = 3; b = 23, c = ‒36, ∆ = 23² ‒ 4.3.(‒36) = 529 + 432 = 961 > 0.

Do đó phương trình có hai nghiệm phân biệt là

- 9

Vậy phương trình có hai nghiệm phân biệt là  _; - 9

b) x² + x = 1

x² + x – 1 = 0

3x² + 8x – 3 = 0 

Ta có: a = 3; b’ = 4, c = ‒3, ∆’ = 4² ‒ 3.(‒3) = 16 + 9 = 25 > 0.

Do đó phương trình có hai nghiệm phân biệt là

- 3

Vậy phương trình có hai nghiệm phân biệt là   _; - 3

c) Xét phương trình 7x² – 2x + 1 = 0 

Ta có: a = 7; b′ = – ; c = 1; ∆’ = (– )² - 7 . 1 = 7 – 7 = 0 

Do đó phương trình có nghiệm kép là  =

d) x(2x + 5) = x² – 9.

2x² + 5x – x² + 9 = 0

x² + 5x + 9 = 0

Ta có: a = 1, b = 5, c = 9, ∆ = 5² – 4.1.9 = 25 – 36 = ‒11 < 0.

Do đó phương trình đã cho vô nghiệm.

Bài tập 17 (trang 18):

Giải các phương trình:

a) x² – (3 +

b) (2x – 5)(3x + 2) = (5x + 1)(3x + 2);

c) x² + x = (x + 1) 

Bài giải chi tiết: 

a) Xét phương trình x² – (3 +

có = = 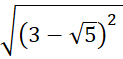| 3 -  | =

Khi đó phương trình có hai nghiệm phân biệt là 

3

b) (2x – 5)(3x + 2) = (5x + 1)(3x + 2)

(2x – 5)(3x + 2) ‒ (5x + 1)(3x + 2) = 0

(3x + 2)(2x ‒ 5 ‒ 5x ‒ 1) = 0

(3x + 2)(‒3x ‒ 6) = 0

3x + 2 = 0 hoặc ‒3x ‒ 6 = 0

x =  hoặc x = -2

Vậy phương trình có hai nghiệm là x =  hoặc x = -2

c) x² + x = (x + 1)

x (x + 1) - (x + 1) = 0 

(x + 1) (x - ) = 0 

x + 1 = 0 hoặc x -  = 0 

x = -1 hoặc x =

Vậy phương trình có hai nghiệm x = -1 hoặc x =

Bài tập 18 (trang 18):

Tìm hai số u và v (nếu có) trong mỗi trường hợp sau:

a) u + v = –2, uv = –35;

b) u + v = 8, uv = 105;

c) u + v = –1; u² + v² = 25.

Bài giải chi tiết: 

a) u và v là hai nghiệm của phương trình x² + 2x – 35 = 0.

Phương trình trên có a = 1, b’ = 1, c = ‒25, ∆ = 1² ‒ 1.(‒35) = 1 + 35 = 36 > 0.

Do đó, phương trình có hai nghiệm phân biệt là

5

-7 

Vậy u = 5; v = –7 hoặc u = –7; v = 5.

b) Ta có S = 8, P = 105 nên S² – 4P = 8² – 4.105 = 64 – 420 = ‒356 < 0.

Do đó không có hai số u và v thoả mãn điều kiện đã cho.

c) Ta có (u + v)² = u² + 2uv + v² = (u² + v²) + 2uv.

Suy ra (–1)² = 25 + 2uv

Hay 2uv = –24

Do đó uv  = –12.

Với u + v = –1, uv = –12 ta có u và v là hai nghiệm của phương trình x² + x ‒ 12 = 0.

Phương trình trên có a = 1, b = 1, c = ‒12, ∆ = 1² ‒ 4.1.(‒12) = 1 + 48 = 49 > 0.

Do đó, phương trình có hai nghiệm phân biệt là

3

- 4 

Vậy u = 3; v = – 4 hoặc u = – 4; v = 3.

Bài tập 19 (trang 18):

Cho phương trình 2x² – 9x – 5 = 0. Gọi x₁, x₂ là hai nghiệm của phương trình. Không giải phương trình, hãy tính giá trị của các biểu thức sau:

a) A = ^2 2 - 2 ² - 2 ²

b) B =  +

Bài giải chi tiết: 

Xét phương trình 2x² – 9x – 5 = 0.

Phương trình trên có a = 2, b = –9, c = –5 và ∆ = (–9)² – 4.2.( –5) = 81 + 40 = 121 > 0.

Do đó phương trình đã cho có hai nghiệm phân biệt.

Theo định lí Viète, ta có: 

S =  =  ₌   

P =  =

a) A =  ^2 2 - 2 ² - 2 ²

= ² – 2 [ ² - 2]

Thay ₌   và = = vào biểu thức trên, ta được: 

A =

b) B =  +

=

Thay ₌   và = = vào biểu thức trên, ta được: 

B =

Bài tập 20 (trang 18):

Cho phương trình 5x² – 7x + 1 = 0. Gọi x₁, x₂ là hai nghiệm của phương trình. Không giải phương trình, hãy tính giá trị của biểu thức

A =  ² 

Bài giải chi tiết: 

Xét phương trình 5x² – 7x + 1 = 0 có ∆ = (–7)² – 4.5.1 = 49 – 20 = 29 > 0.

Do đó phương trình đã cho có hai nghiệm phân biệt.

Theo định lí Viète, ta có:

=  =

=

Thay vào phương trình A ta được A =

Bài tập 21 (trang 18):

Một công nhân theo kế hoạch phải làm 120 sản phẩm trong một thời gian nhất định. Do cải tiến kĩ thuật nên thực tế mỗi ngày người đó đã làm được nhiều hơn 3 sản phẩm so với kế hoạch. Vì thế người đó đã hoàn thành công việc sớm hơn dự định 2 ngày. Hỏi theo kế hoạch, mỗi ngày công nhân đó phải làm bao nhiêu sản phẩm?

Bài giải chi tiết: 

Gọi x là số sản phẩm mà người công nhân phải làm theo kế hoạch mỗi ngày (x ∈ ℕ^*, x < 120).

Số sản phẩm mỗi ngày mà người đó đã làm theo thực tế là x + 3 (sản phẩm).

Thời gian mà người đó phải hoàn thành theo kế hoạch là  (ngày) 

Thời gian mà người đó phải hoàn thành theo kế hoạch là (ngày)

Theo bài, người đó đã hoàn thành công việc sớm hơn dự định 2 ngày nên ta có phương trình:

Giải phương trình: 

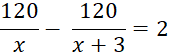
60(x + 3) – 60x = x(x + 3)

60x + 180 – 60x = x² + 3x

x² + 3x ‒180 = 0

Phương trình trên có a = 1, b = 3, c = ‒180, ∆ = 3² ‒ 4.1.(‒180) = 9 + 720 = 729 > 0.

Do đó, phương trình có hai nghiệm phân biệt là x = 12 và x = -15 

Ta thấy chỉ có giá trị x₁ = 12 thoả mãn điều kiện.

Vậy theo kế hoạch, mỗi ngày công nhân đó phải làm 12 sản phẩm.

Bài tập 22 (trang 18):

Một mảnh vườn hình chữ nhật có diện tích 1 000 m². Nếu tăng chiều dài thêm 10 m, giảm chiều rộng đi 5 m thì diện tích mảnh vườn không thay đổi. Tính các kích thước của mảnh vườn.

Bài giải chi tiết: 

Gọi x (m) là chiều dài của mảnh vườn (x > 0).

Do mảnh vườn hình chữ nhật có diện tích 1 000 m² nên chiều rộng của mảnh vườn là (m)

Nếu tăng chiều dài thêm 10 m thì chiều dài của mảnh vườn lúc sau là x + 10 (m). 

Nếu giảm chiều rộng đi 5 m thì chiều rộng của mảnh vườn lúc sau là  – 5 (m)

Diện tích của mảnh vườn khi đó là:

 (x + 10) ( – 5) 

Theo bài, sau khi thay đổi kích thước thì diện tích mảnh vườn không thay đổi, nên ta có phương trình: (x + 10) ( – 5) = 1000

Giải phương trình ta được: 

(x + 10) ( – 5) = 1000

‒x² + 2 000 ‒ 10x = 0

x² + 10x ‒ 2 000 = 0

Phương trình trên có a = 1, b’ = 5, c = ‒2 000, ∆’ = 5² – 1.(‒2 000) = 2 025 > 0.

Do đó phương trình có hai nghiệm phân biệt là x = 40 hoặc x = -50 

Ta thấy chỉ có giá trị x₁ = 40 thoả mãn điều kiện.

Vậy chiều dài của mảnh vườn là 40 m, chiều rộng của mảnh vườn 25 m. 

Bài tập 23 (trang 19):

Một ô tô dự định đi từ tỉnh A đến tỉnh B cách nhau 180 km trong một thời gian nhất định. Sau khi đi được 1 giờ, ô tô bị hỏng nên phải dừng lại 20 phút để sửa. Để đến tỉnh B đúng giờ đã định thì trên quãng đường còn lại ô tô phải tăng tốc độ thêm mỗi giờ 12 km. Tính tốc độ lúc đầu của ô tô.

Bài giải chi tiết: 

Gọi x (km/h) là tốc độ lúc đầu của ô tô (x > 0).

Thời gian dự định đi từ A đến B là (giờ)

Quãng đường ô tô đi được sau 1 giờ là: x (km).

Quãng đường còn lại sau khi đi được 1 giờ là 180 – x (km).

Vận tốc ô tô đi quãng đường còn lại là: x + 12 (km/h).

Thời gian đi quãng đường lúc sau là  (giờ)

Theo bài, ô tô dừng lại 20 phút = giờ để sửa chữa và vẫn đến tỉnh B đúng giờ đã định nên ta có phương trình: 

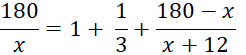
Giải phương trình ta có: 

180.3(x + 12) – (180 – x).3x = 4x(x + 12)

540x + 6 480 – 540x + 3x² = 4x² + 48x

x² + 48x ‒ 6 480 = 0

Phương trình trên có a = 1, b’ = 24, c = ‒ 6 480, ∆’ = 24² – 1.(‒6 480) = 7 056 > 0.

Do đó phương trình có hai nghiệm phân biệt là x = 60 hoặc x = -180 

Ta thấy chỉ có giá trị x₁ = 60 thỏa mãn điều kiện.

Vậy tốc độ ban đầu của ô tô là 60 km/h.

Bài tập 24 (trang 19):

Một phòng họp có 420 cái ghế được chia thành các dãy có số ghế bằng nhau. Nếu thêm cho mỗi dãy 7 cái ghế và bớt đi 5 dãy thì số ghế trong phòng họp không thay đổi. Hỏi lúc đầu trong phòng họp có bao nhiêu dãy ghế?

Bài giải chi tiết: 

Gọi số dãy ghế của phòng họp lúc đầu là x (dãy) (x ∈ ℕ*).

Số ghế ở mỗi dãy lúc đầu là (cái)

Nếu bớt đi 5 dãy thì số dãy ghế lúc sau là: x – 5 (dãy).

Do số ghế trong phòng họp không thay đổi nên số ghế ở mỗi dãy lúc sau là (cái)

Do lúc sau đã thêm cho mỗi dãy 7 cái ghế so với ban đầu nên ta có phương trình: 

+ 7

Giải phương trình ta có: 

60x – 60(x – 5) = x(x – 5)

60x ‒ 60x + 300 = x² ‒ 5x

x² ‒ 5x ‒ 300 = 0

Phương trình trên có a = 1, b = ‒5, c = ‒300, ∆ = (‒5)² – 4.1.(‒300) = 1 225 > 0.

Do đó phương trình có hai nghiệm phân biệt là: x = 20 hoặc x = -15 

Ta thấy chỉ có giá trị x₁ = 20 thỏa mãn điều kiện.

Vậy lúc đầu trong phòng họp có 20 dãy ghế.

Bài tập 25 (trang 19):

Người ta trộn 8 g chất lỏng A với 6 g chất lỏng B để được hỗn hợp có khối lượng riêng là 0,7 g/cm³. Biết khối lượng riêng của chất lỏng A lớn hơn khối lượng riêng chất lỏng B là 0,2 g/cm³. Tìm khối lượng riêng của mỗi chất lỏng.

Bài giải chi tiết: 

Gọi x (g/cm³) là khối lượng riêng của chất lỏng B (x > 0,0).

Khối lượng riêng của chất lỏng A là x + 0,2 (g/cm³).

Thể tích của chất lỏng B là  

Thể tích của chất lỏng A là  

Khối lượng của hỗn hợp chất lỏng sau khi trộn là: 8 + 6 = 14 (g).

Thể tích của hỗn hợp chất lỏng sau khi trộn là:  

Khi đó, ta có phương trình:  

Giải phương trình ta được 

8x + 6(x + 0,2) = 20x(x + 0,2)

8x + 6x + 1,2 = 20x² + 4x

20x² – 10x – 1,2 = 0.

Phương trình trên có a = 20, b’ = ‒5, c = –1,2; ∆ = (‒5)² ‒ 20.(–1,2) = 25 + 24 = 49 > 0.

Do đó, phương trình có hai nghiệm phân biệt là x = 0,6 hoặc x = -0,1 

Ta thấy chỉ có giá trị x₁ = 0,6 thoả mãn điều kiện,

Vậy khối lượng riêng của chất lỏng B là 0,6 g/cm³; của chất lỏng A là 0,8 g/cm³.