CHƯƠNG 2: BẤT ĐẲNG THỨC. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN.

BÀI TẬP CUỐI CHƯƠNG 2

Bài tập 1 trang 33 sách bài tập Toán 9 Tập 1: Cho a, b, c là ba số thỏa mãn a > b và b > c. Khẳng định nào sau đây đúng?

A. a > c.

B. c > a.

C. a ≤ c.

D. c ≥ a.

Bài giải chi tiết: 

Đáp án đúng là: A

Từ a > b, b > c ta có a > c.

Bài tập 2 trang 33 sách bài tập Toán 9 Tập 1: Cho số thực x thoả mãn x2 < 9. Khẳng định nào sau đây đúng?

A. x < 3 hoặc x > –3.

B. x < –3 hoặc x > 3.

C. x < 3 và x > –3.

D. x < –3 và x > 3.

Bài giải chi tiết: 

Đáp án đúng là: C

Ta có:

x² < 9

x² – 9 < 0

(x – 3)(x + 3) < 0

Do đó x – 3 và x + 3 trái dấu nhau.

Lại có x – 3 < x + 3 nên x – 3 < 0 và x + 3 > 0

Suy ra x < 3 và x > –3.

Bài tập 3 trang 33 sách bài tập Toán 9 Tập 1: Nếu a < b và c < 0 thì khẳng định nào sau đây đúng?

A. ac < bc.

B. ac² > bc².

C. ac³ < bc³.

D. ac > bc.

Bài giải chi tiết: 

Đáp án đúng là: D

Nếu a < b và c < 0 thì ac > bc.

Bài tập 4 trang 34 sách bài tập Toán 9 Tập 1: Trong các giá trị sau của y, giá trị nào nhỏ nhất thỏa mãn bất đẳng thức 2y + 10 ≥ 25?

A. 5.

B. 7.

C. 8.

D. 10.

Bài giải chi tiết: 

Đáp án đúng là: C

Ta có:

2y + 10 ≥ 25

2y ≥ 25 ‒10

2y ≥ 15

y ≥ 7,5.

Vậy giá trị nhỏ nhất thỏa mãn bất đẳng thức 2y + 10 ≥ 25 là 8.

Bài tập 5 trang 34 sách bài tập Toán 9 Tập 1: Trong các giá trị sau của z, giá trị nào lớn nhất thỏa mãn bất đẳng thức
A. 2.

B. 4.

C. 5.

D. 6.

Bài giải chi tiết: 

Đáp án đúng là: B

Ta có:

 3z ‒ 5 < 8

 3z < 13

z <

Vậy giá trị lớn nhất thỏa mãn bất đẳng thức là 4.

Bài tập 6 trang 34 sách bài tập Toán 9 Tập 1: Trong các giá trị sau của w, giá trị nào nhỏ nhất thỏa mãn bất đẳng thức

A. 8.

B. 10.

C. 12.

D. 14.

Bài giải chi tiết:

Đáp án đúng là: A

Ta có:

3w + 1 > 15

3w > 14

w >

Vậy giá trị nhỏ nhất trong các phương án và thỏa mãn bất đẳng thức

Bài tập 7 trang 34 sách bài tập Toán 9 Tập 1: Cho ba số a, b, c. Nếu a ≥ b thì:

a) a – c ≥ b – c.

b) ac ≥ bc với c < 0.

c) ac ≥ bc với c > 0.

d) a² ≥ b².

Bài giải chi tiết:

a) Cộng cả hai vế với ‒c ta được:

a ≥ b

a ‒ c ≥ b ‒ c

Vậy ý a) đúng.

b) Do c < 0, nên khi nhân cả hai vế của bất đẳng thức a ≥ b với c, ta được:

ac ≤ bc.

Vậy ý b) sai.

c) Do c > 0, nên khi nhân cả hai vế của bất đẳng thức a ≥ b với c, ta được:

ac ≥ bc.

Vậy ý c) đúng.

d) Ý d) là sai. Chẳng hạn ta có 1 > –2 nhưng 1² < (–2)².

Bài tập 8 trang 34 sách bài tập Toán 9 Tập 1: Cho bất đẳng thức –3x ‒ 1 < 0. (1)

a) Cộng hai vế của (1) với 3, ta được x – 1 < 0.

b) Nhân hai vế của (1) với ta được x –

c) Cộng hai vế của (1) với 1 rồi nhân hai vế của bất đẳng thức nhận được với ta được: x <
d) Cộng hai vế của (1) với 1 rồi nhân hai vế của bất đẳng thức nhận được với -

ta được: x >
Bài giải chi tiết:

Ta có:

⦁ –3x ‒ 1 < 0

–3x ‒ 1 + 3 < 0 + 3 (cộng hai vế của (1) với 3)

‒3x < 1

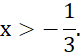
Vậy ý a) sai.

⦁ –3x ‒ 1 < 0

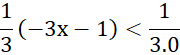
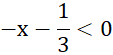
Vậy ý b) sai.

⦁ –3x ‒ 1 < 0

–3x ‒ 1 + 1 < 0 + 1 (cộng hai vế của (1) với 1)

‒3x < 1             

−3x⋅

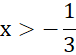
Vậy ý c) sai và ý d) đúng.

Bài tập 9 trang 34 sách bài tập Toán 9 Tập 1: Cho a là số thực dương. Chứng minh rằng nếu a > 1, thì a² > a.

Bài giải chi tiết:

Với a > 1 ta có a > 0.

Nhân hai vế của a > 1 với a > 0, ta được a² > a.

Bài tập 10 trang 34 sách bài tập Toán 9 Tập 1: Cho a, b và c là các số thực sao cho a > 0 và b > c. Chứng minh rằng a(b – c) > 0.
Bài giải chi tiết:

Nhân hai vế của b > c với a > 0, ta được ab > ac.

Trừ hai vế của ab > ac cho ac, ta được ab – ac > 0 hay a(b – c) > 0.

Bài tập 11 trang 34 sách bài tập Toán 9 Tập 1: Chứng minh rằng nếu a > 1 và b > 1 thì a + b > 2.
Bài giải chi tiết:

Cộng hai vế của a > 1 với b, ta được a + b > 1 + b. (1)

Cộng hai vế của b > 1 với 1, ta được 1 + b > 2. (2)

Từ (1) và (2), ta được a + b > 2.

Bài tập 12 trang 34 sách bài tập Toán 9 Tập 1: Cho a, b là hai số thực dương sao cho a > b. Chứng minh rằng

Bài giải chi tiết:

Vì a > 0 và b > 0 nên ab > 0, do đó

Nhân hai vế của a > b với , ta được:

Bài tập 13 trang 34 sách bài tập Toán 9 Tập 1: Bình xăng của một chiếc xe ô tô đang chứa 40 l xăng. Biết rằng nếu xe đi 15 km thì tiêu thụ hết 1 l xăng. Hỏi xe có thể đi được quãng đường tối đa là bao nhiêu kilômét với lượng xăng đó?

Bài giải chi tiết:

Gọi S (km) là quãng đường tối đa mà xe ô tô đi được (S > 0).

Do xe đi 15 km thì tiêu thụ hết 1 l xăng, bình xăng chứa 40 l xăng nên ta có bất phương trình:

S ≤ 15.40

S ≤ 600.

Vậy quãng đường tối đa mà ô tô đi được là 600 km.

Bài tập 14 trang 34 sách bài tập Toán 9 Tập 1: Bạn Mai đi học ở Singapore, bạn ấy đã đạt điểm số của hai môn là 67 và 74 điểm. Muốn có phần thưởng bạn Mai phải đạt môn thứ ba bao nhiêu điểm? Biết rằng muốn đoạt giải thưởng thì điểm trung bình tối thiểu của ba môn phải là 75.

Bài giải chi tiết:

Gọi x là điểm số môn thứ ba bạn Mai phải đạt được (0 < x < 100).

Tổng điểm 3 môn của bạn Mai là: 67 + 74 + x.

Trung bình điểm 3 môn bạn Mai đạt được là:

Do điểm trung bình tối thiểu của ba môn phải là 75 nên ta có bất phương trình:

67 + 74 + x ≥ 75.3

 x ≥ 225 – 67 – 74

x ≥ 84.

Vậy bạn Mai phải đạt tối thiểu 84 điểm ở môn thứ ba để đoạt giải thưởng.

Bài tập 15 trang 35 sách bài tập Toán 9 Tập 1: Bạn Hà định mời 12 bạn thân đi ăn nhân dịp bạn ấy được học bổng. Mỗi bạn có thể chọn một tô mì hay một đĩa gà rán. Một tô mì có giá 36 nghìn đồng, một đĩa gà rán có giá 45 nghìn đồng.

a) Hỏi số tiền nhiều nhất và số tiền ít nhất mà bạn Hà phải chi là bao nhiêu?

b) Nếu bạn Hà có ý định chi không quá 400 nghìn đồng cho bữa tiệc thì số đĩa gà rán nhiều nhất mà các bạn có thể chọn là bao nhiêu? Biết rằng có hai bạn chắc chắn chọn món mì.

Bài giải chi tiết:

a) Gọi x (nghìn đồng) là số tiền bạn Hà phải chi.

Một đĩa gà rán có giá 45 nghìn đồng, vì vậy 12 đĩa gà rán có giá là 12.45 = 540.

Hà phải chi nhiều nhất khi cả 12 bạn đều chọn gà rán, tức là số tiền nhiều nhất Hà phải chi là 540 nghìn đồng.

Một tô mì có giá 36 nghìn đồng, vì vậy 12 tô mì có giá là 12.36 = 432.

Hà chi ít nhất khi cả 12 bạn đều chọn mì, tức là số tiền ít nhất Hà phải chi là 432 nghìn đồng.

b) Gọi x là số đĩa gà rán các bạn chọn thêm.

Có hai bạn chắc chắn chọn món mì nên số tiền chi cho 2 tô mì đó là: 36.2 = 72 (nghìn).

Do số tiền chi ra không quá 400 nghìn, nên số tiền còn lại để bạn Hà chi cho các suất ăn còn lại là: 400 – 72 = 328 (nghìn đồng).

Tức là: x.45 ≤ 328 hay

Vậy số đĩa gà rán được gọi thêm nhiều nhất là 7 đĩa.