CHƯƠNG 5: ĐƯỜNG TRÒN

BÀI 1: ĐƯỜNG TRÒN

Bài tập 1 trang 84 sách bài tập Toán 9 Tập 1: Chứng minh bốn đỉnh của hình vuông ABCD có cạnh bằng 16 cm đều nằm trên một đường tròn. Tính bán kính của đường tròn này.

Bài giải chi tiết: 

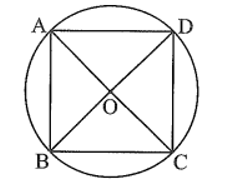
Gọi O là giao điểm của hai đường chéo của hình vuông ABCD, khi đó O là trung điểm của AC và BD, nên OA = OB = OC = OD =

Áp dụng định lí Pythagore cho tam giác ABD vuông tại A ta có:

Do đó OA= OB = OC = OD =

Suy ra bốn đỉnh của hình vuông ABCD đều nằm trên đường tròn (O;8√2 cm).

Bài tập 2 trang 84 sách bài tập Toán 9 Tập 1: Cho tam giác ABC có AB = AC = 13 cm, BC = 10 cm và có BH, CK là hai đường cao.

Chứng minh:

a) Bốn điểm B, C, H, K cùng nằm trên đường tròn (O; R).

b) Điểm A nằm ngoài đường tròn (O; R).

Bài giải chi tiết: 

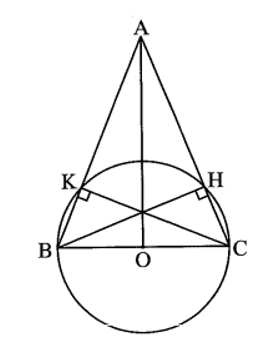
a) Gọi O là trung điểm của BC. Khi đó, OB=OC=

Do BH và CK là đường cao tam giác ABC nên BH ⊥ AC tại H; CK ⊥ AB tại K

Suy ra tam giác BHC vuông tại H; tam giác BKC vuông tại K

Xét tam giác BKC vuông tại H có KO là đường trung tuyến ứng với cạnh huyền BC nên

Chứng minh tương tự đối với ∆BKC vuông tại K, ta có HO=

Suy ra KO=OH=OB=OC=BC=12⋅10=5(cm).

Tứ giác BKHC có: OB = OK = OH = OC = 5 cm nên bốn điểm B, C, H, K cùng nằm trên đường tròn (O; R) với R = 5 cm.

b) Xét ∆ABC cân tại A (do AB = AC) có AO là đường trung tuyến nên đồng thời là đường cao, suy ra ∆ABO vuông tại O.

Áp dụng định lí Pythagore cho tam giác AOB vuông tại O, ta có:

Vì 12 > 5 nên OA > R, suy ra điểm A nằm ngoài đường tròn (O; R).

Bài tập 3 trang 85 sách bài tập Toán 9 Tập 1: Xác định vị trí tương đối của hai đường tròn (O; R) và (O’; R’) trong mỗi trường hợp sau:

a) OO’ = 7, R = 29, R’ = 4;

b) OO’ = 21, R = 44, R’ = 23;

c) OO’ = 15, R = 7, R’ = 8;

d) OO’ = 6, R = 24, R’ = 20.

Bài giải chi tiết: 

a) Ta có: 7 < 29 – 4 nên OO’ < R – R’, suy ra đường tròn (O; R) đựng đường tròn (O’; R’).

b) Ta có: 21 = 44 – 23 nên OO’ = R – R’, suy ra hai đường tròn (O; R) và (O’; R’) tiếp xúc trong.

c) Ta có: 15 = 7 + 8 nên OO’ = R + R’, suy ra hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài.

d) Ta có: 24 – 20 < 6 < 24 + 20 nên R – R’ < OO’ < R + R’, suy ra hai đường tròn (O; R) và (O’; R’) cắt nhau.

Bài tập 4 trang 85 sách bài tập Toán 9 Tập 1: Cho đường tròn (O; 8 cm) và hai điểm A, B nằm trên đường tròn thoả mãn AB = 6 cm. Vẽ đường kính MN sao cho hai đoạn thẳng MN và AB không có điểm chung. Gọi A’, B’ lần lượt là hai điểm đối xứng với A, B qua MN. Chứng minh:

a) ABB’A’ là hình thang cân.

b) Bốn điểm A, B, B’, A’ cùng nằm trên đường tròn (O; 8 cm).

Bài giải chi tiết: 

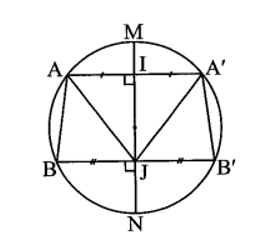
a) Gọi I, J lần lượt là giao điểm của MN với AA’, BB’.

Do A’, B’ lần lượt là hai điểm đối xứng với A, B qua MN nên AA’ ⊥ MN tại I, IA = IA’ và BB’ ⊥ MN tại J, JB = JB’.

Xét ∆AIJ và ∆A’IJ, có:

ˆAIJ=ˆA′IJ=90°,AIJ^=A'IJ^=90°, IA = IA’, cạnh IJ chung

Do đó ∆AIJ  = ∆A’IJ (hai cạnh góc vuông)

Suy ra AJ = A’J và ˆAJI=ˆA′JIAJI^=A'JI^ (các cặp cạnh và góc tương ứng).

Ta có: ˆAJI+ˆBJA=90°;ˆA′JI+ˆA′JB′=90°AJI^+BJA^=90°;  A'JI^+A'JB'^=90° và ˆAJI=ˆA′JIAJI^=A'JI^  nên ˆBJA=ˆA′JB′.BJA^=A'JB'^.

Xét ∆ABJ và ∆A’B’J, có:

JB = JB’,ˆBJA=ˆA′JB′,BJA^=A'JB'^,  AJ = A’J

Do đó ∆ABJ = ∆A’B’J (c.g.c), suy ra ˆB=ˆB′.B^=B'^.

Ta có AA’ // BB’ (cùng vuông góc với MN) nên ABB’A’ là hình thang, lại có ˆB=ˆB′B^=B'^ nên ABB’A’ là hình thang cân.

b) Ta có MN là trục đối xứng của đường tròn (O; 8 cm), A, B đã thuộc đường tròn (O; 8 cm) suy ra A’, B’ là hai điểm đối xứng với A, B qua MN nên cũng thuộc đường tròn (O; 8 cm), suy ra bốn điểm A, B, B’, A’ cùng nằm trên đường tròn (O; 8 cm).

Bài tập 5 trang 85 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) đường kính AB, vẽ dây CD vuông góc với AB tại M. Cho biết AM = 1 cm, CD=2√3 cm. Tính:

a) Bán kính đường tròn (O).

b) Số đo ˆCAB.

Bài giải chi tiết: 

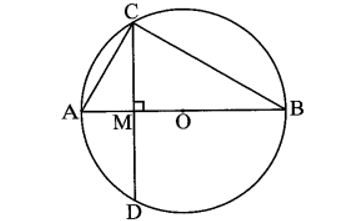
a) Ta có đường kính AB là trục đối xứng của đường tròn (O)

Suy ra MC=MD=

Tam giác ABC có CO là đường trung tuyến và CO=, suy ra ABC là tam giác vuông tại C.
Do ˆCAM+ˆCBM=90°;ˆCAM+ˆACM=90° nên ˆCBM=ˆACM

Xét ∆CMB và ∆AMC có:

ˆAMC=ˆCMB=90° và ˆCBM=ˆACM

Do đó ∆CMB ᔕ ∆AMC (g.g).

Suy ra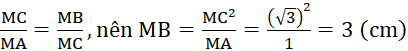

Gọi R là bán kính đường tròn đường kính AB, khi đó AB = 2R.

Ta có AB = MA + MB = 1 + 3 = 4 = 2R, suy ra R = 2 cm.

b) Xét tam giác AMC vuông tại M, ta có:

suy ra ˆCAB≈60°.

Bài tập 6 trang 85 sách bài tập Toán 9 Tập 1: Cho hai điểm A, B trên đường tròn (O; R). Cho biết AB = 9 cm và khoảng cách từ O đến đường thẳng AB là OH

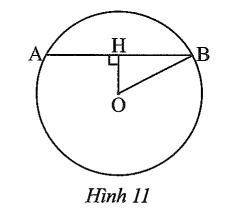
Tính:

a) Số đo ˆOBH.

b) Bán kính R của đường tròn.

Bài giải chi tiết: 

a) Xét tam giác OHB vuông tại H, ta có:

sinˆOBH=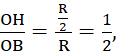  suy ra ˆOBH=30°.

b) Xét tam giác AOB cân tại O (do OB = OA = R) có OH là đường cao nên đồng thời là đường trung tuyến, suy ra HB=HA=

Xét tam giác OHB vuông tại H, ta có:

cosˆOBH = suy ra OB=

Suy ra R=OB=3√3cm. 

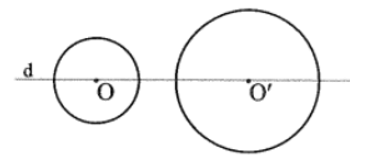
Bài tập 7 trang 85 sách bài tập Toán 9 Tập 1: Tìm trục đối xứng của hình tạo bởi hai đường tròn (O) và (O’) trong Hình 12.

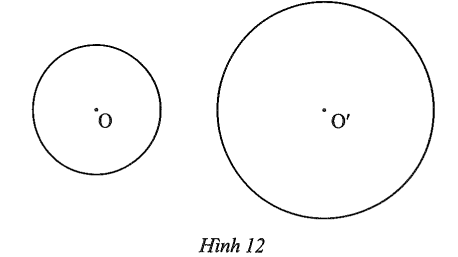
Bài giải chi tiết: 

Vẽ đường thẳng d đi qua tâm O và O’ của hai đường tròn, ta có d là trục đối xứng của (O) và (O’), suy ra d là trục đối xứng của hình tạo bởi hai đường tròn (O) và (O’).

Bài tập 8 trang 85 sách bài tập Toán 9 Tập 1: Cho hình vuông ABCD có cạnh bằng 4 cm.

a) Vẽ các đường tròn tâm A, B, C, D bán kính 2 cm.

b) Nêu nhận xét về vị trí giữa các cặp đường tròn (A; 2 cm) và (B; 2 cm), (A; 2 cm) và (C; 2 cm).

Bài giải chi tiết:

a)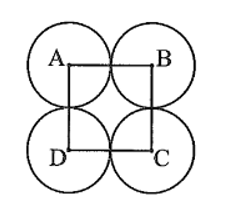

b) Ta có AB = 4 = 2 + 2, suy ra cặp đường tròn (A; 2 cm) và (B; 2 cm) tiếp xúc ngoài.

Do ABCD là hình vuông nên AD = DC = 4 cm và ˆADC=90°,  áp dụng định lí Pythagore cho ∆ADC vuông tại D, ta có:

Mà AC = 4√2 > 2 + 2, suy ra cặp đường tròn (A; 2 cm) và (C; 2 cm) ở ngoài nhau.