CHƯƠNG 9

BÀI TẬP CUỐI CHƯƠNG 9

Bài tập 1 (trang 87):

Cho tam giác vuông ABC có độ dài hai cạnh góc vuông là 5 cm, 12 cm. Bán kính R của đường tròn ngoại tiếp tam giác ABC có độ dài là

A. 13 cm.

B. 10 cm.

C. 5 cm.

D. 6,5 cm.

Bài giải chi tiết: 

Đáp án đúng là: D

Do ∆ABC vuông có hai cạnh góc vuông là 5 cm, 12 cm nên áp dụng định lí Pythagore, ta có độ dài cạnh huyền bằng: = = 13 (cm)

Bán kính của đường tròn ngoại tiếp tam giác ABC có độ dài là  = 6,5(cm)

Câu 2 (trang 87):

Tam giác đều cạnh bằng 8a có bán kính đường tròn nội tiếp là

A. 4a.

B. 2a.

C. 4a

D. 2a

Bài giải chi tiết: 

Đáp án đúng là: A

Bán kính đường tròn nội tiếp tam giác đều cạnh 8a là = =4a.

Câu 3 (trang 87):

Cho tứ giác MNPQ nội tiếp đường tròn (O; R) và =63°=. Số đo của là

A. 63°.

B. 117°.

C. 63°.

D. 126°

Bài giải chi tiết: 

Đáp án đúng là: B

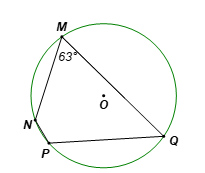
Do tứ giác MNPQ nội tiếp đường tròn (O; R) nên tổng hai góc đối bằng 180°

Suy ra  + =180

Do đó =180°−=180°−63°=117°.

Câu 4 (trang 87):

Cho tứ giác ABCD nội tiếp đường tròn (O; R). Biết  =90°, BD = 12 cm. Độ dài của bán kính R là

A. 12 cm.

B. 24 cm.

C. 6 cm.

D. 6cm.

Bài giải chi tiết: 

Đáp án đúng là: C

Tam giác ABD có = 90°  nên ∆ABD vuông tại A, do đó AD là đường kính của đường tròn ngoại tiếp ∆ABD hay chính là đường tròn (O; R).

Suy ra bán kính của đường tròn (O; R) là R= .BD = . 12 =6 (cm).

Vậy độ dài của bán kính R của đường tròn (O; R) là 6 cm.

Câu 6 (trang 88):

Cho tứ giác ABCD nội tiếp đường tròn (E). Số đo của các cung được cho trong Hình 2. Số đo của  là

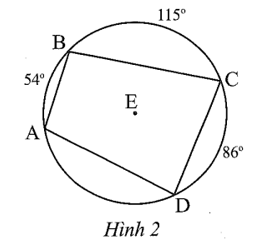
A. 201°.

B. 100,5°.

C. 159°.

D. 79,5°.

Bài giải chi tiết: 

Đáp án đúng là: D

Từ Hình 2, ta có: sđ  = 54°, sđ  = 115°, sđ = 86°

Mà ,   lần lượt là góc nội tiếp của các cung ,  nên =  =⋅115°=57,5°, =  =⋅ 86° = 43°.

Suy ra  =  +  =57,5°+43°=100,5°.

Do tứ giác ABCD nội tiếp đường tròn (E) nên hai góc đối nhau của tứ giác bằng 180°, hay  +  =180°.

Suy ra =180° − =180°−100,5°=79,5°.

Câu 7 (trang 88):

Số đo của  trong Hình 3 là

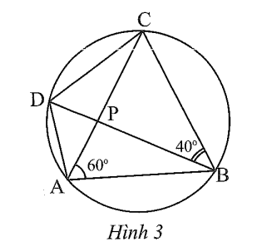
A. 100°.

B. 160°.

C. 80°.

D. 120°.

Bài giải chi tiết: 

Đáp án đúng là: C

Ta có  ,   là hai góc nội tiếp cùng chắn cung CD của đường tròn trong Hình 3, nên   =   = 40°.>

Suy ra    +  =40°+60°=100°

Tứ giác ABCD nội tiếp đường tròn nên hai góc đối nhau của tứ giác bằng 180°, hay  + = 180

Suy ra  = 180°-  = 180°-100° = 80°

Câu 8 (trang 88):

Gọi A, B, C là ba đỉnh liên tiếp của một đa giác đều có 10 cạnh. Số đo của  là

A. 144°.

B. 36°.

C. 72°.

D. 152°.

Bài giải chi tiết: 

Đáp án đúng là: A

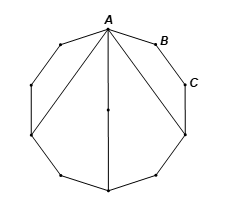
Ta có đa giác đều 10 cạnh là đa giác có 10 góc bằng nhau.

Tổng các góc của đa giác đều này bằng tổng các góc của 4 tứ giác và bằng: 4.360° = 1 440°.

Khi đó số đo mỗi góc của đa giác đều 10 cạnh là:  =144°.

Do A, B, C là ba đỉnh liên tiếp của đa giác đều 10 cạnh nên    là một góc của đa giác đều đó, suy ra   =144°.

Câu 9 (trang 88):

Cho hình vuông ABCD có O là giao điểm của hai đường chéo. Phép quay tâm O biến hình vuông ABCD thành chính nó có góc quay là

A. 45°.

B. 90°.

C. 135°.

D. 210°.

Bài giải chi tiết: 

Đáp án đúng là: B

Vì ABCD là hình vuông có O là giao điểm của hai đường chéo nên O là tâm của hình vuông.

Do đó các phép quay biến hình vuông ABCD thành chính nó là các phép quay 90°, 180°, 270°, 360° tâm O cùng chiều hoặc ngược chiều kim đồng hồ.

Vậy ta chọn phương án B.

Câu 10 (trang 88):

Cho tam giác ABC ngoại tiếp đường tròn (I; r); D, E, F lần lượt là các tiếp điểm của cạnh AB, BC, AC với đường tròn (I; r) (Hình 4).

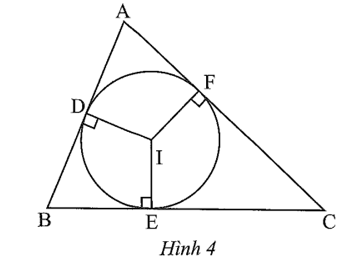
a) Ba đường trung trực của tam giác ABC cắt nhau tại I.

b) AD = AF

c) BD + CF = BC.

d) IE = r.

Bài giải chi tiết: 

⦁ Do tam giác ABC ngoại tiếp đường tròn (I; r) hay đường tròn (I; r) nội tiếp ∆ABC, nên ba đường phân giác của các góc A, B, C cắt nhau tại I. Do đó ý a) là sai.

⦁ Ta có D, F lần lượt là các tiếp điểm của cạnh AB, AC với đường tròn (I; r) nên AD, AF là hai tiếp tuyến của đường tròn (I; r). Suy ra AD = AF (tính chất hai tiếp tuyến cắt nhau). Do đó ý b) là đúng.

⦁ Tương tự ta cũng chứng minh được: BD = BE và CE = CF.

Suy ra BD + CF = BE + CE = BC. Do đó ý c) là đúng.

⦁ Vì D, E, F lần lượt là các tiếp điểm của cạnh AB, BC, AC với đường tròn (I; r) nên ID = IE = IF = r.

Vậy:

a) S;

b) Ð;

c) Đ;

d) Ð.

Câu 11 (trang 88):

Cho tứ giác ABCD nội tiếp đường tròn (O) có =80° và =52° (Hình 5).

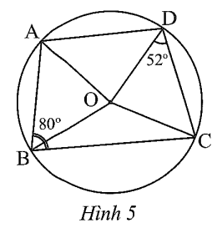
a) 160°.

b) =160°.

c)  =84°.

d)  =86°.

Bài giải chi tiết: 

⦁ Vì tứ giác ABCD nội tiếp đường tròn (O) nên +   =180°

Suy ra =180°−=180°−80°=100°.

Do đó ý a) là sai.

⦁ Xét đường tròn (O) có ,  lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung AC, suy ra = 2⋅80°=160°. Do đó ý b) là đúng.

⦁ Ta có = - =100°−52°=48°.

Xét ∆OAD cân tại O (do OA = OD) nên = =48°

Suy ra = 180°−−=180°−48°−48°=84°.

Do đó ý c) là đúng.

⦁ Tương tự như trên ta cũng có ∆OCD cân tại O nên

=180°−2=180°−2⋅52°=76°.

Do đó ý d) là sai.

Vậy:

a) S;

b) Đ;

c) Ð;

d) S.

Câu 12 (trang 89):

Cho bát giác đều có tâm O và AB là một cạnh, OH là đoạn vuông góc kẻ từ O đến AB.

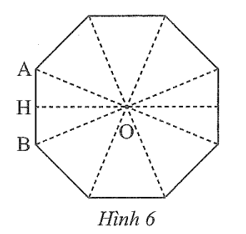
a) =50°

b) OH = OA.sin 45°.

c) Phép quay 90° tâm O biến bát giác đều thành chính nó.

d) AB = 2OA.sin 22,5°.

Bài giải chi tiết: 

⦁ Ta có bát giác đều nội tiếp đường tròn (O; OA) và chia đường tròn này thành 8 cung có số đo bằng nhau, suy ra  =45°.

Do đó ý a) là sai.

⦁ Ta có ∆OAB cân tại O (do OA = OB) nên = = =  =67,5°.

Xét ∆OAH vuông tại H, ta có:

OH=OA⋅sin = OA ⋅  sin67,5°

Do đó ý b) là sai.

⦁ Các phép quay biến bát giác đều thành chính nó là các phép quay 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360° tâm O cùng chiều và ngược chiều kim đồng hồ.

Do đó ý c) là đúng.

⦁ Xét ∆OAB cân tại O có OH là đường cao nên đồng thời là đường phân giác và đường trung tuyến của tam giác.

Suy ra ==  ⋅ 45° = 22,5° và H là trung điểm của AB nên AB = 2AH.

∆OAH vuông tại H, ta có:

AH=OA⋅sin = OA⋅sin22,5°.

Suy ra AB = 2OA.sin22,5°. Do đó ý d) là đúng.

Vậy:

a) S;

b) S;

c) Đ;

d) Đ.

Bài tập 13 (trang 89):

Cho tam giác ABC có (O) là đường tròn ngoại tiếp. Vẽ đường cao AH của tam giác ABC và đường kính AD của đường tròn (O). Biết AB = 8 cm; AC = 15 cm và AH = 5 cm.

a) Chứng minh ∆AHB ᔕ ∆ACD.

b) Tính độ dài bán kính của đường tròn.

Bài giải chi tiết: 

⦁ Từ A, B lần lượt kẻ AH, BK vuông góc với CD (H, K ∈ CD).

Ta có AH ⊥ CD, AB // CD nên AH ⊥ AB.

Xét ∆AHD và ∆BKC có:

==90°, AD = BC và    (do ABCD là hình thang cân)

Do đó ∆ADH = ∆BCK (cạnh huyền – góc nhọn)

Suy ra DH = CK (hai cạnh tương ứng).

⦁ Xét tứ giác ABKH có:  = = =90° nên ABKH là hình chữ nhật.

Gọi E, F lần lượt là trung điểm của AB và HK.

Suy ra EF là đường trung trực của AB và HK.

Ta có DH = CK và HF = KF nên DF = CF, do đó F là trung điểm của DC.

Suy ra EF cũng là đường trung trực của CD.

⦁ Gọi M là trung điểm của AD. Vẽ đường trung trực MO của AD, MO cắt EF tại O.

Khi đó, O nằm trên đường trung trực của AB, AD, DC nên OA = OB, OA = OD, OD = OC

Suy ra OA = OB = OC = OD hay A, B, C, D cùng thuộc đường tròn (O; OA).

Vậy hình thang cân ABCD nội tiếp đường tròn (O; OA).

Bài tập 14 (trang 89):

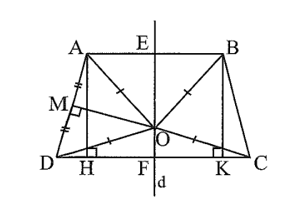
⦁ Từ A, B lần lượt kẻ AH, BK vuông góc với CD (H, K ∈ CD).

Ta có AH ⊥ CD, AB // CD nên AH ⊥ AB.

Xét ∆AHD và ∆BKC có:

==90°, AD = BC và    (do ABCD là hình thang cân)

Do đó ∆ADH = ∆BCK (cạnh huyền – góc nhọn)

Suy ra DH = CK (hai cạnh tương ứng).

⦁ Xét tứ giác ABKH có:  = = =90° nên ABKH là hình chữ nhật.

Gọi E, F lần lượt là trung điểm của AB và HK.

Suy ra EF là đường trung trực của AB và HK.

Ta có DH = CK và HF = KF nên DF = CF, do đó F là trung điểm của DC.

Suy ra EF cũng là đường trung trực của CD.

⦁ Gọi M là trung điểm của AD. Vẽ đường trung trực MO của AD, MO cắt EF tại O.

Khi đó, O nằm trên đường trung trực của AB, AD, DC nên OA = OB, OA = OD, OD = OC

Suy ra OA = OB = OC = OD hay A, B, C, D cùng thuộc đường tròn (O; OA).

Vậy hình thang cân ABCD nội tiếp đường tròn (O; OA).

Bài tập 15 (trang 89):

Cho tam giác nhọn ABC(AB < AC) có hai đường cao BD và CE.

a) Chứng minh bốn điểm B, C, D, E cùng thuộc một đường tròn.

b) Vẽ đường tròn (B; BD). Chứng minh AC là tiếp tuyến của đường tròn (B; BD).

c) Đường tròn (B; BD) cắt CE tại K(K nằm giữa E và C). Qua D vẽ đường thẳng vuông góc với BC tại H và cắt đường thẳng AB tại M. Chứng minh =

Bài giải chi tiết: 

a) Ta có BD ⊥ AC, CE ⊥ AB nên tam giác BEC vuông tại E và tam giác BDC vuông tại D.

∆BEC vuông tại E nên nội tiếp đường tròn đường kính BC. (1)

∆BDC vuông tại D nên nội tiếp đường tròn đường kính BC. (2)

Từ (1) và (2) suy ra bốn điểm B, C, D, E cùng thuộc đường tròn đường kính BC.

b) Ta có BD là bán kính đường tròn (B; BD) và BD ⊥ AC nên AC là tiếp tuyến của đường tròn (B; BD).

c) Xét ∆BHD và ∆BDC có:

Góc B chung; = =90°

Do đó ∆BHD ᔕ ∆BDC (g.g)

Suy ra   =  hay BD² = BH.BC.

Ta lại có BD = BK (bán kính đường tròn (B; BD)) nên BK² = BH.BC.

Suy ra   =

Xét ∆BHK và ∆BKC có:

Góc B chung;  =

Do đó ∆BHK ᔕ ∆BKC (c.g.c)

Suy ra = (hai góc tương ứng).

Mà = (cùng phụ với ˆABC)ABC^)  nên =

Bài tập 16 (trang 89):

Cho đường tròn tâm O, đường kính AB. Gọi C là điểm chính giữa của cung AB. Trên đoạn thẳng AB lấy điểm E sao cho BE = AC. Tia AC và tia BD cắt nhau tại M. Vẽ EH vuông góc với AC tại H. Tia phân giác của góc ˆBACBAC^ cắt EH tại K và cắt đường tròn (O) tại D. Tia CK cắt AB tại I và cắt đường tròn (O) tại F.

a) Chứng minh EH // BC.

b) Tính số đo của

c) Chứng minh =

d) Chứng minh I là trung điểm của đoạn thẳng AE.

Bài giải chi tiết: 

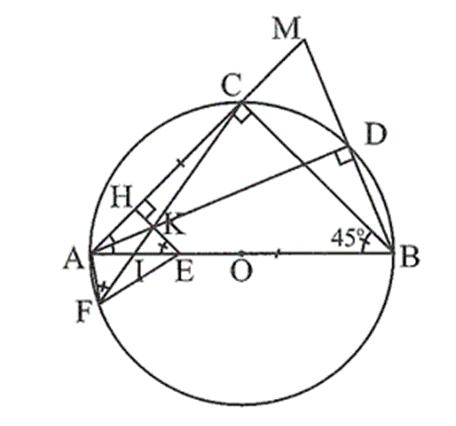
a) Ta có  = 90° (góc nội tiếp chắn nửa đường tròn (O) đường kính AB), suy ra BC ⊥ AC.

Mà EH ⊥ AC (giả thiết), suy ra EH // BC.

b) Vì C là điểm chính giữa của cung AB và AB là đường kính của đường tròn (O), suy ra sđ  =  sđ   = sđ  =  ⋅ 180°=90°.

Vì AD là tia phân giác của ˆBACBAC^ (giả thiết) nên = =  , suy ra sđ  =  sđ   = sđ  =  ⋅ 90° = 45°.

Xét đường tròn (O) có:

⦁   là góc nội tiếp chắn cung CB nên  = sđ  =  ⋅ 90° = 45°;

⦁   là góc nội tiếp chắn cung CA nên  = sđ  =  ⋅ 90° = 45°;

⦁  là góc nội tiếp chắn cung CD nên  = sđ  =  ⋅ 45° = 22,5°;

Suy ra  = 45°; = + =22,5°+45°=67,5°.

Xét ∆MAB có: +  +   = 180°

Suy ra  =180°−  −   =180°−45°−67,5°=67,5°.

c) Vì EH // BC nên = (hai góc đồng vị).

Mà  = (góc nội tiếp cùng chắn cung AC của đường tròn (O)).

Suy ra =

d) Tam giác AIC có AK là tia phân giác của , suy ra =    

Tam giác CIB có EK // CB, suy ra  =  (định lí Thalès)

Từ (1) và (2) suy ra =

Mà AC = BE (giả thiết) nên  AI = IE.

Vậy I là trung điểm của đoạn thẳng AE.

Bài tập 17 (trang 89):

 Một công viên hình tam giác được bao quanh bởi ba con đường ML, LN, NM với kích thước (tính theo mét) được ghi trên bản vẽ trong Hình 7. Người ta muốn dựng một trụ đèn tại một điểm cách đều ba con đường. Xác định vị trí điểm cần tìm và tính khoảng cách từ điểm đó đến ba con đường.

Bài giải chi tiết: 

Điểm O là điểm cần tìm để dựng trụ đèn và là tâm của đường tròn nội tiếp tam giác MNL.

Khoảng cách r từ O đến ba con đường là bán kính của đường tròn nội tiếp tam giác MNL.

Áp dụng định lí Pythagore vào tam giác OLH vuông tại H, ta có:

OL² = OH² + HL²

Suy ra r=  OH =  =  =  =5 (m).