CHƯƠNG 8

 BÀI 2. XÁC XUẤT CỦA BIẾN CỐ

Bài tập 1 (trang 65): 

Bác Mạnh rút ngẫu nhiên 1 lá bài từ bộ bài tây 52 lá. Tính xác suất của mỗi biến cố sau:

A: “Bác Mạnh rút được lá bài Át”;

B: “Bác Mạnh rút được lá bài chất cơ”.

Bài giải chi tiết: 

Do bộ bài có 52 lá nên số các kết quả có thể xảy ra là n(Ω) = 52.

Do các lá bài giống nhau nên các kết quả của phép thử có cùng khả năng xảy ra.

a) Do có 4 lá Át trong bộ bài nên số kết quả thuận lợi cho biến cố A là n(A) = 4.

Xác suất của biến cố A là P(A)=  =  =  

b) Do có 13 lá bài chất cơ trong bộ bài nên số các kết quả thuận lợi cho biến cố B là n(B) = 13.

Xác suất của biến cố B là P(B)=  =  = 0,25

Bài tập 2 (trang 65):  Bạn Khuê viết ngẫu nhiên một số tự nhiên chẵn có 4 chữ số lên bảng

a) Có tất cả bao nhiêu kết quả có thể xảy ra của phép thử trên?

b) Tính xác suất của mỗi biến cố sau:

A: “Số được viết có 4 chữ số giống nhau”;

B: “Số được viết lớn hơn hoặc bằng 5 000”.

Bài giải chi tiết: 

Các số tự nhiên chẵn có 4 chữ số là: 1 000; 1 002; 1 004; …; 9 998.

a) Số các số tự nhiên chẵn có 4 chữ số là (9 998 ‒ 1 000) : 2 + 1 = 4 500.

Do đó số kết quả có thể xảy ra của phép thử trên là n(Ω) = 4 500.

b) ⦁ Có 4 số tự nhiên chẵn có 4 chữ số giống nhau là: 2 222; 4 444; 6 666; 8 888.

Số kết quả thuận lợi cho biến cố A là n(A) = 4.

Xác suất của biến cố A là P(A)=   =  =

⦁ Các số tự nhiên chẵn có 4 chữ số và lớn hơn hoặc bằng 5 000 là: 5 000; 5 002; …; 9 998.

Số các số chẵn có 4 chữ số và lớn hơn hoặc bằng 5 000 là:

(9 998 ‒ 5 000) : 2 + 1 = 2 500.

Số kết quả thuận lợi cho biến cố B là n(B) = 2 500.

Xác suất của biến cố B là P(B)=   =  = .

Bài giải chi tiết: 

Cô giáo thống kê điểm kiểm tra môn Tin học của các học sinh lớp 9A ở bảng sau:

Chọn ngẫu nhiên 1 học sinh lớp 9A. Biết rằng có 4 học sinh lớp 9A được 10 điểm.

a) Xác định số kết quả có thể xảy ra của phép thử.

b) Tính xác suất của biến cố A: “Học sinh được chọn đạt trên 8 điểm”.

   Bài giải chi tiết: 

a) Số học sinh của lớp 9A là: 4 : 10% = 40 (học sinh).

Số kết quả có thể xảy ra của phép thử là n(Ω) = 40.

b) Tần số tương đối của các học sinh được chọn đạt trên 8 điểm là: 30% + 10% = 40%.

Số học sinh đạt trên 8 điểm là: 40 . 40% = 16 (học sinh).

Số kết quả thuận lợi cho biến cố A là n(A) = 16.

Xác suất của biến cố A là P(A)=  = 0,4

Bài tập 4 (trang 66):  

Ở một trường Trung học cơ sở, tỉ lệ học sinh khối 6, 7, 8, 9 lần lượt là 28%, 25%, 25% và 22%. Chọn ngẫu nhiên 1 học sinh của trường. Tính xác suất của mỗi biến cố sau:

A: “Học sinh được chọn thuộc khối 6”;

B: “Học sinh được chọn thuộc khối 7”.

Bài giải chi tiết: 

Gọi N là tổng số học sinh của trường.

Số học sinh khối 6 của trường là: N . 28% = 0,28N (học sinh).

Số học sinh khối 7 của trường là N . 25% = 0,25N (học sinh).

Khi thực hiện phép thử chọn ngẫu nhiên 1 học sinh của trường, số kết quả có thể xảy ra là n(Ω) = N.

⦁ Số kết quả thuận lợi cho biến cố A là n(A) = 0,28N.

Xác suất của biến cố A là P(A)=   =  = 0.28

⦁ Số kết quả thuận lợi cho biến cố B là n(B) = 0,25N.

Xác suất của biến cố B là P(B)=   = =  0,25.

Bài tập 5 (trang 66): 

Bảng sau ghi lại điểm thi môn Tiếng Anh của 10 học sinh Tổ 1.

Chọn ngẫu nhiên một học sinh của Tổ 1. Tính xác suất của mỗi biến cố sau:

A: “Học sinh được chọn được 9 điểm”;

B: “Học sinh được chọn được trên 7 điểm”.

Bài giải chi tiết: 

Số kết quả có thể xảy ra là n(Ω) = 10.

⦁ Có 3 học sinh được điểm 9 nên số kết quả thuận lợi cho biến cố A là n(A) = 3.

Xác suất của biến cố A là P(A) =   = =  0,3.

⦁ Có 7 học sinh được trên 7 điểm nên số các kết quả thuận lợi cho biến cố B là n(B) = 7.

Xác suất của biến cố B là P(B)=   = =  0,7.

Bài tập 6 (trang 66): 

Kết quả kiểm tra tình trạng cân nặng của các bạn học sinh lớp 9B được thống kê lại ở bảng sau:

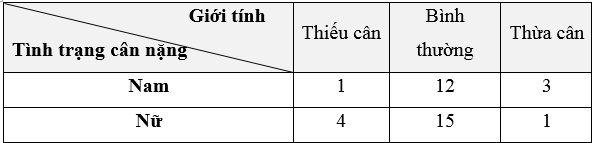
Chọn ngẫu nhiên 1 học sinh của lớp 9B. Tính xác suất của mỗi biến cố sau:

A: “Học sinh được chọn là học sinh nữ và có cân nặng bình thường”;

B: “Học sinh được chọn bị thừa cân”;

C: “Học sinh được chọn là học sinh nam”.

Bài giải chi tiết: 

Tổng số học sinh là: 1 + 12 + 3 + 4 + 15 + 1 = 36 (học sinh).

Số các kết quả có thể xảy ra là n(Ω) = 36.

⦁ Số học sinh nữ có cân nặng bình thường là 15 nên số kết quả thuận lợi cho biến cố A là n(A) = 15.

Xác suất của biến cố A là P(A)=   =  =

⦁ Số học sinh bị thừa cân là: 3 + 1 = 4 (học sinh).

Số kết quả thuận lợi cho biến cố B là n(B) = 4.

Xác suất của biến cố B là P(B)=   =   =

⦁ Số học sinh nam là 1 + 12 + 3 = 16 (học sinh).

Số kết quả thuận lợi cho biến cố C là n(C) = 16.

Xác suất của biến cố C là P(C)=   =  =

Bài tập 7 (trang 66): 

Bạn Bách có 10 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 10. Bách chọn ngẫu nhiên một tấm thẻ, xem số trên thẻ và thay số đó vào vị trí của dấu ? trong phương trình sau:

x² + 4x + ? = 0 (*)

Tính xác suất của biến cố A: “Phương trình (*) có nghiệm”.

Bài giải chi tiết: 

Số kết quả có thể xảy ra là n(Ω) = 10. Do các thẻ cùng loại nên các kết quả có cùng khả năng xảy ra.

Gọi số được viết vào vị trí dấu ? là m.

Khi đó phương trình (*) trở thành: x² + 4x + m = 0.

Phương trình này có ∆’ = 2² – 1.m = 4 – m.

Phương trình (*) có nghiệm khi ∆’ ≥ 0, tức là 4 – m ≥ 0 hay m ≤ 4.

Do đó khi thay dấu ? bằng các giá trị từ 1 đến 10 ta thấy chỉ có các giá trị 1, 2, 3, 4 làm cho phương trình (*) có nghiệm.

Vậy số kết quả thuận lợi cho biến cố A là n(A) = 4.

Xác suất của biến cố A là P(A)=   =  = 0,4

Bài tập 8 (trang 67): 

Bác Dũng có một cái khoá số như hình bên. Bác Dũng chọn ngẫu nhiên một dãy gồm 4 chữ số để đặt làm mã số mở khoá.

Tính xác suất của các biến cố:

A: “4 chữ số được chọn giống nhau”;

B: “4 chữ số được chọn lập thành một số có 4 chữ số”;

C: “4 chữ số được chọn có tổng bằng 35”.

Bài giải chi tiết: 

Dãy số dùng để đặt mã số là các số từ 0000 đến 9999.

Số kết quả có thể xảy ra là n(Ω) = 10 000 kết quả.

⦁ Các kết quả thuận lợi cho biến cố A là 0000, 1111, ..., 9999.

Số kết quả thuận lợi cho biến cố A là n(A) = 10.

Xác suất của biến cố A là P(A)=  = 0, 001

⦁ Các kết quả thuận lợi cho biến cố B là 1000, 1001, …, 9999.

Số kết quả thuận lợi cho biến cố B là n(B) = 9 000.

Xác suất của biến cố B là P(B)=  = 0,9

⦁ Tổng của 4 chữ số bằng 35 khi trong 4 chữ số đó có 3 chữ số 9 và 1 chữ số 8.

Các kết quả thuận lợi cho biến cố C là 8999, 9899, 9989, 9998.

Số kết quả thuận lợi cho biến cố C là n(C) = 4.

Xác suất của biến cố C là P(C)=   = 0, 0004