CHƯƠNG 1: PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH

BÀI 1: PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN

Bài tập 1 trang 7 sách bài tập Toán 9 Tập 1: Giải các phương trình:

a) 7x(2x – 5) = 0

b) (3x – 6)(4x + 9) = 0

c) (x−2)(x+3) = 0

d) (1,5t – 6)(0,3t + 9) = 0

Bài giải chi tiết: 

a) 7x(2x – 5) = 0

7x = 0 hoặc 2x ‒ 5 = 0

x = 0 hoặc x =

Vậy phương trình đã cho có hai nghiệm là x = 0 và x =

b) (3x – 6)(4x + 9) = 0

3x ‒ 6 = 0 hoặc 4x + 9 = 0

x = 2 hoặc x =

Vậy phương trình đã cho có hai nghiệm là x = 2 và x =

c) (x−2)(x+3) = 0

x−2 = 0 hoặc x +3 = 0

x = 2 hoặc x = -3

x =  hoặc x = –12

Vậy phương trình đã cho có hai nghiệm là x =   và x = –12.

d) (1,5t – 6)(0,3t + 9) = 0

1,5t ‒ 6 = 0 hoặc 0,3t + 9 = 0

t = 4 hoặc t = –30.

Vậy phương trình đã cho có hai nghiệm là t = 4 và t = –30.

Bài tập 2 trang 7 sách bài tập Toán 9 Tập 1: Giải các phương trình:

a) 5x(x – 3) + 2(x – 3) = 0;

b) 7x(x + 4) – 3x – 12 = 0;

c) x² – 2x – (5x – 10) = 0;

d) (5x – 2)² – (x + 8)² = 0.

Bài giải chi tiết: 

a) 5x(x – 3) + 2(x – 3) = 0

(x – 3)(5x + 2) = 0

x – 3 = 0 hoặc 5x + 2 = 0

x = 3 hoặc x =

Vậy phương trình đã cho có hai nghiệm là x = 3 và x =

b) 7x(x + 4) –3x – 12 = 0 

7x(x + 4) – 3(x + 4) = 0

(x + 4)(7x – 3) = 0

x + 4 = 0 hoặc 7x – 3 = 0

x = –4 hoặc x =

Vậy phương trình đã cho có hai nghiệm là x = –4  và x =

c)  x² – 2x – (5x – 10) = 0

x(x – 2) – 5(x – 2) = 0

(x – 2)(x – 5) = 0

x – 2 = 0 hoặc x – 5 = 0

x = 2 hoặc x = 5.

Vậy phương trình đã cho có hai nghiệm là x = 2 hoặc x = 5.

d) (5x – 2)² – (x + 8)² = 0

(5x – 2 + x + 8)(5x – 2 – x – 8) = 0

(6x + 6)(4x – 10) = 0

6x + 6 = 0 hoặc 4x – 10 = 0

x = –1 hoặc x =

Vậy phương trình đã cho có hai nghiệm là x = –1 hoặc x =

Bài tập 3 trang 8 sách bài tập Toán 9 Tập 1: Giải các phương trình:

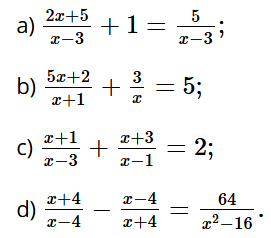
Bài giải chi tiết: 

Bài tập 4 trang 8 sách bài tập Toán 9 Tập 1: Một phân số có tử số bé hơn mẫu số 9 đơn vị. Nếu thêm tử số 1 đơn vị và thêm mẫu số 2 đơn vị thì được phân số mới bằng . Tìm phân số đã cho.

Bài giải chi tiết: 

Gọi x là tử số của phân số đã cho (x ∈ ℤ).

Mẫu số của phân số là x + 9.

Khi đó ta có phân số đã cho là . Để phân số này có nghĩa thì x + 9 ≠ 0, tức là x ≠ –9.

Nếu thêm tử số 1 đơn vị thì ta được tử số của phân số mới là x + 1.

Nếu thêm mẫu số 2 đơn vị ta được mẫu số của phân số mới là x + 9 + 2 = x + 11.

Lúc này, ta có phân số mới là .

Theo bài, phân số mới bằng  nên ta có phương trình: =

Giải phương trình:

x = 4 (thoả mãn điều kiện x ∈ ℤ và x ≠ –9).

Do đó phân số đã cho có tử số là 4, mẫu số là 4 + 9 = 13. 

Vậy phân số phải tìm là

Bài tập 5 trang 8 sách bài tập Toán 9 Tập 1: Một vòi nước chảy vào một bể không có nước. Cùng lúc đó một vòi khác chảy từ bể ra mỗi giờ lượng nước chảy ra bằng lượng nước chảy vào. Sau 5 giờ nước trong bể đạt dung tích bể. Hỏi nếu bể không có nước mà chỉ mở vòi chảy vào thì sau bao lâu đầy bể?

Bài giải chi tiết: 

Gọi x (giờ) là thời gian vòi chảy vào đầy bể (x > 0).

Trong 1 giờ vòi chảy nước vào được bể.

Lượng nước chảy ra trong 1 giờ là

Như vậy, sau 1 giờ thì lượng nước có trong bể là:

Sau 5 giờ, lượng nước có trong bể là: 5( (bể).

heo bài, Sau 5 giờ nước trong bể đạt dung tích bể nên ta có phương trình:

5( =

x = 8 (thoả mãn điều kiện).

Vậy nếu bể không có nước mà chỉ mở vòi chảy vào thì sẽ đầy bể trong 8 giờ.

Bài tập 6 trang 8 sách bài tập Toán 9 Tập 1: Một nhóm thợ đóng giày dự định hoàn thành kế hoạch trong 26 ngày. Nhưng do cải tiến kĩ thuật nên mỗi ngày đã vượt mức 6 đôi giày, do đó chẳng những nhóm thợ đã hoàn thành kế hoạch đã định trong 24 ngày mà còn vượt mức 104 đôi giày. Tính số đôi giày nhóm thợ phải làm theo kế hoạch.

Bài giải chi tiết: 

Gọi x là số đôi giày mà nhóm thợ đóng được mỗi ngày theo kế hoạch (x ∈ ℕ*).

Số đôi giày đóng được theo kế hoạch trong 26 ngày là 26x (đôi giày).

Số đôi giày mỗi ngày đóng được thực tế là x + 6 (đôi giày).

Tổng số đôi giày đóng được thực tế là 26x + 104 (đôi giày).

Thời gian nhóm thợ đã hoàn thành theo thực tế là: (ngày).

Vì nhóm thợ hoàn thành công việc trong 24 ngày nên ta có phương trình:

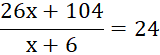
Giải phương trình: 

26x + 104 = 24(x + 6)

26x + 104 = 24x + 144

2x = 40

x = 20 (thoả mãn điều kiện).

Vậy số đôi giày phải làm theo kế hoạch là 26.20 = 520 (đôi giày).

Bài tập 7 trang 8 sách bài tập Toán 9 Tập 1: Một người dự định đi bằng ô tô trên quãng đường AB dài 120 km trong một thời gian nhất định. Nửa quãng đường đầu xe đi vào đường cao tốc với tốc độ hơn dự định 15 km/h. Sau khi ra khỏi đường cao tốc, trên nửa quãng đường còn lại, xe đi với tốc độ chậm hơn dự định 10 km/h. Biết ô tô đến đúng giờ dự định. Tính thời gian dự định đi quãng đường AB của người đó.

Bài giải chi tiết: 

Gọi x (km/h) là tốc độ ô tô dự định đi quãng đường AB (x > 0).

Xe đi nửa quãng đường đầu với tốc độ là x + 15 (km/h).

Xe đi nửa quãng đường sau với tốc độ là x – 10 (km/h).

Thời gian ô tô dự định đi là:

Nửa quãng đường AB là: 120 : 2 = 60 (km).

Thời gian ô tô đi nửa quãng đường đầu là: (giờ).

Thời gian ô tô đi nửa quãng đường sau là: (giờ).

Do ô tô đến đúng giờ dự định nên ta có phương trình: 

Giải phương trình:

2(x + 15)(x – 10) = x(x – 10) + x(x + 15)

2(x² – 10x + 15x – 150) = x² – 10x + x² + 15x

2x² + 10x – 300 = 2x² + 5x

5x = 300

x = 60 (thoả mãn điều kiện).

Vậy thời gian ô tô dự định đi quãng đường AB là = 2 (giờ).