BÀI 2. XÁC SUẤT CỦA BIẾN CỐ

KHỞI ĐỘNG

Bạn Dương xoay tấm bìa hình tròn như hình bên và quan sát xem khi tấm bìa dừng lại, mũi tên chỉ vào hình quạt tròn ghi số nào. Kết quả 20 lần quay được ghi ở bảng

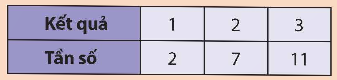
Các kết quả 1; 2; 3 có cùng khả năng xảy ra không? Tại sao?

Giải rút gọn:

Các kết quả 1; 2; 3 không cùng khả năng xảy ra. 

Vì diện tích các phần là không bằng nhau.

1. KẾT QUẢ ĐỒNG KHẢ NĂNG

Hoạt động 1 (trang 57):

Các kết quả của một phép thử sau có cùng khả năng xảy ra không? Tại sao?

a) Gieo một đồng xu cân đối và đồng chất.

b) Lấy ngẫu nhiên 1 viên bi từ một hộp có 10 viên bi giống nhau được đánh số từ 1 đến 10.

c) Lấy ngẫu nhiên 1 tấm thẻ từ một hộp chứa 2 tấm thẻ ghi số 5 và 5 tấm thẻ ghi số 2 và xem số của nó

Giải rút gọn:

a) Các kết quả của phép thử có cùng khả năng xảy ra vì khả năng gieo ra mặt sấp và ngửa là như nhau.

b) Các kết quả của phép thử không cùng khả năng xảy ra vì các viên bi giống nhau và có số thứ tự không lặp lại

c) Các kết quả của phép thử không cùng khả năng xảy ra vì số tấm thẻ ghi số 2 và số 5 là khác nhau

Thực hành 1 (trang 58):

Kết quả của mỗi phép thử sau có đồng khả năng không? Tại sao?

a) Rút ngẫu nhiên 1 tấm thẻ từ 10 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 10.

b) Chọn ngẫu nhiên 1 học sinh từ danh sách lớp.

c) Lấy ra ngẫu nhiên 1 viên bi từ một hộp chứa 1 viên bi xanh, 1 viên bi đỏ và 8 viên bi trắng rồi quan sát màu của nó, biết rằng các viên bi có cùng kích thước và khối lượng.

Giải rút gọn:

a) Do các tấm thẻ là cùng loại và số thứ tự không lặp lại nên có cùng khả năng được chọn. 

Các kết quả của phép thử là đồng khả năng.

b) Do mỗi học sinh có những điều kiện trạng thái khác nhau nên các kết quả của phép thử là không đồng khả năng.

c) Do trong hộp có 3 màu bi, mỗi màu có số lượng khác nhau nên không khả năng được chọn. 

Các kết quả của phép thử không đồng khả năng.

Vận dụng 1 (trang 58):

Kết quả của mỗi phép thử sau có đồng khả năng không? Tại sao?

a) Gặp ngẫu nhiên 1 người ở Đồng Tháp và hỏi xem người đó sinh ở huyện/ thành phố nào. 

b) Rút ngẫu nhiên 1 lá bài từ bộ bài tây 52 lá.

Giải rút gọn:

a) Do mỗi người có quê quán ở những nơi khác nhau nên không có cùng khả năng được chọn. 

Các kết quả của phép thử không đồng khả năng.

b) Do các lá bài đến từ cùng một bộ bài nên có cùng khả năng được chọn.

 Các kết quả của phép thử là đồng khả năng.

2. XÁC SUẤT CỦA BIẾN CỐ

Hoạt động 2 (trang 58):

Bạn An gieo một con xúc xắc cân đối và đồng chất. Bạn Trung tung một đồng xu cân đối và đồng chất. So sánh khả năng xảy ra của các biến cố sau:

A: “An gieo được mặt có chẵn chấm”;

B: “An gieo được mặt có 2 chấm”;

C: “Trung tung được mặt sấp”.

Giải rút gọn:

- Số kết quả có thể xảy ra với phép thử của An: 6 

- Số kết quả có thể xảy ra với phép thử của Trung: 2 

- 3 kết quả thuận lợi cho biến cố A là: 2 chấm; 4 chấm; 6 chấm.

Khả năng xảy ra của biến cố A là: .100% = 50%.

- 1 kết quả thuận lợi cho biến cố B là: 2 chấm.

Khả năng xảy ra của biến cố B là: .100% = 16,67%.

- 1 kết quả thuận lợi cho biến cố C là: mặt sấp.

Khả năng xảy ra của biến cố C là: .100% = 50%.

Vậy khả năng xảy ra của biến cố A và C là bằng nhau và lớn hơn khả năng xảy ra của biến cố B.

Thực hành 2 (trang 60):

Một hộp chứa 4 tấm thẻ cùng loại được đánh số 1; 4; 7; 9. Bạn Khuê và bạn Hương lần lượt mỗi người lấy ra 1 tấm thẻ từ hộp. Tính xác suất của mỗi biến cố sau:

A: “Tích các số ghi trên 2 tấm thẻ là số lẻ”;

B: “Tổng các số ghi trên 2 tấm thẻ là số lẻ”;

C: “Số ghi trên tấm thẻ của bạn Khuê nhỏ hơn số ghi trên tấm thẻ của bạn Hương”.

Giải rút gọn:

Do 4 tấm thẻ là cùng loại nên các thẻ có cùng khả năng được chọn. 

= {(1; 4), (1; 7), (1; 9), (4;1), (4; 7), (4; 9), (7; 1), (7; 4), (7; 9), (9; 1), (9; 4); (9; 7)} 

n() = 12.

- 6 kết quả thuận lợi cho biến cố A là: (1; 7), (1; 9), (7; 1), (9; 1), (7; 9), (9; 7).

n(A) = 6

P(A) = = 0,5.

- 6 kết quả thuận lợi cho biến cố B là: (1; 4), (4; 1), (7; 9), (9; 7), (4; 9), (9; 4).

n(B) = 6

P(B) = = 0,5.

- 6 kết quả thuận lợi cho biến cố C là: (7; 1), (7; 4), (4; 1), (9; 1), (9; 4), (9; 7)

n(C) = 6

P(C) = = 0,5.

Vận dụng 2 (trang 60):

Bạn Thắng có n tấm thẻ cùng loại được đánh số từ 1 đến n. Bạn Thắng rút ngẫu nhiên 1 tấm thẻ. Biết rằng xác suất của biến cố “Lấy được tấm thẻ ghi số có một chữ số là 0,18. Hỏi bạn Thắng có bao nhiêu tấm thẻ?

Giải rút gọn:

n() = n.

Có 9 kết quả thuận lợi cho biến cố là: 1; 2; 3; 4; 5; 6; 7; 8; 9. 

P = = 0,18 n = 50 (tấm thẻ).

3. GIẢI BÀI TẬP CUỐI SÁCH

Bài 1 (trang 60):

Gieo hai con xúc xắc cân đối và đồng chất. Xét hai biến cố sau:

A: “Xuất hiện hai mặt có cùng số chấm”;

B: “Tổng số chấm trên hai con xúc xắc lớn hơn 8”.

Biến cố nào có khả năng xảy ra cao hơn?

Giải rút gọn:

= {(i; j) | 1 i 6, 1 j 6, i; j N}.

n() = 36

Vì xúc xắc cân đối và đồng chất nên nó cùng khả năng xảy ra.

- Có 6 kết quả thuận lợi cho biến cố A là: (1;1), (2;2), (3;3), (4;4), (5;5), (6;6)

n(B) = 6

P(A) = .

- Có 10 kết quả thuận lợi cho biến cố B là: (3;6), (4;5), (4;6), (5;4), (5;5), (5;6), (6;3), (6;4), (6;5), (6;6)

n(B) = 10

P(B) = .

Do nên biến cố B có khả năng xảy ra cao hơn.

Bài 2 (trang 60):

Một chiếc hộp có chứa 5 tấm thẻ cùng loại, được đánh số lần lượt là 3; 5; 6; 7; 9.

Lấy ngẫu nhiên đồng thời 2 tấm thẻ từ hộp.

a) Xác định không gian mẫu và số kết quả có thể xảy ra của phép thử.

b) Tính xác suất của mỗi biến cố sau:

A: “Tích các số ghi trên 2 tấm thẻ chia hết cho 3”;

B: “Tổng các số ghi trên 2 tấm thẻ lớn hơn 13”;

Giải rút gọn:

a) = {(3; 5), (3; 6), (3; 7), (3;9), (5; 6), (5; 7), (5; 9), (6; 7), (6; 9), (7; 9)}. 

n() = 10

b) Do 5 tấm thẻ là cùng loại nên các thẻ có cùng khả năng xảy ra.

- Có 9 kết quả thuận lợi cho biến cố A là: (3; 5), (3; 6), (3; 7), (3;9), (5; 6), (5; 9), (6; 7), (6; 9), (7; 9). 

n() = 9

P(A) = = 0,9.

- Có 3 kết quả thuận lợi cho biến cố B là: (5; 9), (6; 9), (7; 9). 

n() = 3

P(B) = = 0,3.

Bài 3 (trang 61):

Một chiếc hộp chứa 1 viên bi xanh, 1 viên bi đỏ và 1 viên bi trắng. Các viên bi có cùng kích thước và khối lượng. Dung lần lượt lấy ra ngẫu nhiên từng viên bi từ trong hộp cho đến khi hết bi.

a) Xác định không gian mẫu của phép thử.

b) Tính xác suất của mỗi biến cố sau:

A: “Viên bi màu xanh được lấy ra cuối cùng”;

B: “Viên bi màu trắng được lấy ra trước viên bi màu đỏ”;

C: “Viên bi lấy ra đầu tiên không phải là bi màu trắng”;

Giải rút gọn:

a) = {(xanh; đỏ; trắng), (xanh; trắng; đỏ), (trắng; xanh; đỏ), (trắng; đỏ; xanh), (đỏ; xanh; trắng), (đỏ; trắng; xanh)} 

n() = 6 

b) Do 3 viên bi có cùng kích thước và khối lượng nên chúng có cùng khả năng xảy ra.

- Có 2 kết quả thuận lợi cho biến cố A là: (trắng; đỏ; xanh), (đỏ; trắng; xanh).

n() = 2

P(A) = .

- Có 3 kết quả thuận lợi cho biến cố B là: (xanh; trắng; đỏ), (trắng; xanh; đỏ), (trắng; đỏ; xanh).

n(B) = 3

P(B) = = 0,5.

- Có 4 kết quả thuận lợi cho biến cố C là: (xanh; đỏ; trắng), (xanh; trắng; đỏ), (đỏ; xanh; trắng), (đỏ; trắng; xanh).

n() = 4

P(C) = .

Bài 4 (trang 61):

Một túi chứa 3 viên bi màu xanh và một số viên bi màu đỏ có cùng kích thước và khối lượng. Bạn Luân lấy ra ngẫu nhiên 1 viên bi. Biết rằng xác suất của biến cố “Lấy được viên bi màu xanh” là 0,6. Hỏi trong túi có tổng bao nhiêu viên bi?

Giải rút gọn:

Có 3 kết quả thuận lợi cho biến cố : “Lấy được viên bi màu xanh” là: viên bi xanh 1; viên bi xanh 2; viên bi xanh 3. 

n() = 3

P = = 0,6 n = 5 (viên bi).