BÀI 1. ĐƯỜNG TRÒN

1. KHÁI NIỆM ĐƯỜNG TRÒN

Hoạt động 1 (trang 75): Mở một chiếc compa sao cho hai đầu compa cách nhau một khoảng R cho trước. Tì đầu nhọn của compa lên một điểm O cố định trên tờ giấy, xoay compa để đầu bút M của compa vạch trên giấy một đường cong. Nêu nhận xét về các khoảng cách từ một điểm M tuỳ ý trên đường cong vừa vẽ đến điểm O.

Giải rút gọn:

Nhận xét: Khoảng cách từ một điểm M tuỳ ý trên đường cong vừa vẽ đến điểm O là không đổi và bằng R.

2. TÍNH ĐỐI XỨNG CỦA ĐƯỜNG TRÒN

Hoạt động 2 (trang 76):

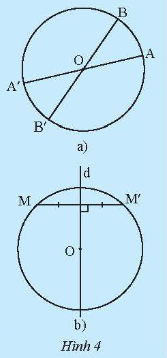
a) Cho đường tròn (O; R).

i) Lấy điểm A nằm trên đường tròn. Vẽ đường thẳng AO cắt đường tròn tại điểm A' khác A. Giải thích tại sao O là trung điểm của đoạn thẳng AA'.

ii) Lấy điểm B khác A thuộc đường tròn (O; R). Tìm điểm B' sao cho O là trung điểm của đoạn thẳng BB'. Điểm B' có thuộc đường tròn (O; R) không? Giải thích.

b) Cho đường tròn (O; R), d là đường thẳng đi qua tâm O. Lấy điểm M nằm trên đường tròn. Vẽ điểm M' sao cho d là đường trung trực của đoạn thăng MM' (khi M thuộc d thì lấy M' trùng với M). Điểm M' có thuộc đường tròn (O; R) không? Giải thích.

Giải rút gọn:

a)

i) Vì A và A' nằm trên đường tròn (O; R), nên OA = OA' = R

=> O là trung điểm của đoạn thẳng AA', 

ii) Vì O là trung điểm của đoạn thẳng BB', nên OB = OB' = R

=> B' thuộc đường tròn (O; R).

b) Vì d là đường trung trực của đoạn thẳng MM', nên OM’ = OM = R

=> M' thuộc đường tròn (O; R).

Thực hành 1 (trang 77): Xác định tâm đối xứng và trục đối xứng của bánh xe trong Hình 7. Giải thích cách làm.

Giải rút gọn:

Tâm đối xứng của đường tròn là tâm của đường tròn

 => Tâm đối xứng của bánh xe chính là điểm O

Trục đối xứng của đường tròn là đường kính của đường tròn 

=> Trục đối xứng là  một đường thẳng bất kì đi qua tâm

Vận dụng 1 (trang 77): Nêu cách chia một cái bánh có dạng hình tròn tâm O (Hình 8) thành hai phần bằng nhau.

Giải rút gọn:

Kẻ một đường thẳng đi qua tâm O của chiếc bánh sẽ được 2 phần bằng nhau

3. ĐƯỜNG KÍNH VÀ DÂY CUNG CỦA ĐƯỜNG TRÒN

Hoạt động 3 (trang 77): Trên đường tròn (O; R), lấy bốn điểm A, B, M, N sao cho AB đi qua O và MN không đi qua O (Hình 9).

a) Tính độ dài đoạn thẳng AB theo R. 

b) So sánh độ dài của MN và OM + ON. Từ đó, so sánh độ dài của MN và AB.

Giải rút gọn:

a) AB = OA + OB = R + R = 2R

b) OM + ON = R + R = 2R

Xét tam giác OMN: MN < OM + ON

=> MN < 2R 

=> MN < AB

Thực hành 2 (trang 78): Cho đường tròn (I) có các dây cung AB, CD, EF. Cho biết AB và CD đi qua tâm I, EF không đi qua I (hình 11). Hãy so sánh độ dài AB, CD, EF

Giải rút gọn:

AB = AI + BI = R + R = 2R

CD = CI + ID = R + R = 2R

IE + EF = 2R

Xét tam giác EIF: EF < IE + IF 

=> AB = CD = 2R > EF

Vận dụng 2 (trang 78): Bạn Mai căng ba đoạn chỉ AB, CD, EF có độ dài lần lượt là 16 cm, 14 cm và 20 cm trên một khung thêu hình tròn bán kính 10 cm (Hình 12). Trong ba dây trên, dây nào đi qua tâm của đường tròn? Giải thích?

Giải rút gọn:

Dây EF đi qua tâm của đường tròn vì EF = 20 = 2.10 = 2R

4. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN

Hoạt động 4 (trang 78): Tìm số điểm chung của hai đường tròn (O) và (O’) trong mỗi trường hợp sau(Hình 13)

Giải rút gọn:

Số điểm chung của hai đường tròn (O) và (O’) là:

a) 0

b) 0

c) 1, điểm chung là M

d) 2, điểm chung là M và N

Hoạt động 5 (trang 79): Cho 2 đường tròn phân biệt (O; R) và (O’; R) với R R’

So sánh OO’ với R+ R’ và R – R’ trong mỗi trường hợp sau đây: (Hình 15 ;Hình 16 và Hình 17)

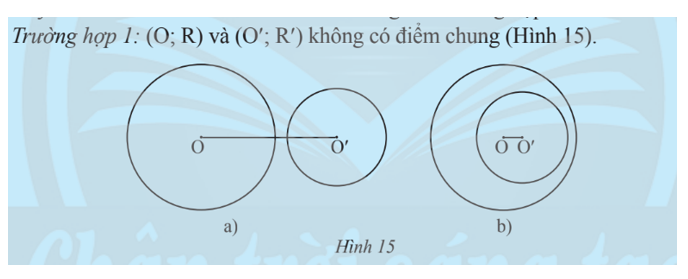
Giải rút gọn:

Trường hợp 1:

a) OO’ > R + R’; OO’ > R – R’

b) OO’ < R + R’; OO’ < R – R’

Trường hợp 2:

a) OO’ = R + R’; OO’ > R – R’

b) OO’ < R + R’; OO’ = R – R’

Trường hợp 3:

OO’ < R + R’; OO’ > R – R’

Thực hành 3 (trang 79): Xác định vị trí tương đối giữa hai đường tròn (I; R) và (J;R’) trong mỗi trường hợp sau :

a) IJ = 5; R = 3; R’ = 2

b) IJ = 4; R = 11; R’ = 7

c) IJ = 6; R = 9; R’ = 4

d) IJ = 10; R = 4; R’ = 1

Giải rút gọn:

a)R + R' = 3 + 2 = 5 = IJ, nên hai đường tròn này tiếp xúc ngoài.

b) R - R' = 11 - 7 = 4 = IJ, nên hai đường tròn này tiếp xúc trong.

c) R + R' = 9 + 4 = 13

R - R' = 9 - 4 = 5

R - R’ < IJ < R + R’ (5 < 6 < 13), nên hai đường tròn này cắt nhau.

d) R + R' = 4 + 1 = 5

R - R' = 4 - 1 = 3

IJ > R + R’ (10 > 5), nên hai đường tròn này không cắt nhau.

Vận dụng 3 (trang 80): Mô tả vị trí tương đối giữa mỗi cặp đường tròn trong hình chụp bộ cồng chiêng Tây Nguyên trong Hình 18.

Giải rút gọn:

a) Hai đường tròn không cắt nhau

b) Hai đường tròn cắt nhau tại 1 điểm (tiếp xúc ngoài)

c) Hai đường tròn cắt nhau tại 2 điểm

5. GIẢI BÀI TẬP CUỐI SÁCH

Bài 1 (trang 81): Cho đường tròn (O), bán kính 5 cm và bốn điểm A, B, C, D thoả mãn OA = 3 cm, OB = 4 cm, OC = 7 cm, OD = 5 cm. Hãy cho biết mỗi điểm A, B, C, D nằm trong, nằm trên hay nằm ngoài đường tròn (O).       

Giải rút gọn:

OA < R (3 < 5), nên điểm A nằm trong đường tròn (O).

OB < R (4 < 5), nên điểm B nằm trong đường tròn (O).

OC > R (7 > 5), nên điểm C nằm ngoài đường tròn (O).

OD = R = 5 cm, nên điểm D nằm trên đường tròn (O).

Bài 2 (trang 80): Cho hình chữ nhật ABCD có AD = 18cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Giải rút gọn:

Gọi O là giao điểm của 2 đường chéo AC và BD

Do ABCD là hình chữ nhật nên:

+ AC = BD

+ O là trung điểm của AC và BD

=> OA = OC = OB = OD (đpcm)

Bán kính đường tròn là: = = 3 cm

Bài 3 (trang 80): Cho tam giác ABC có hai đường cao BB' và CC’. Gọi O là trung điểm của BC.

a) Chứng minh đường tròn tâm O bán kính OB' đi qua B, C, C';

b) So sánh độ dài hai đoạn thẳng BC và B'C'.

Giải rút gọn:

a)Tam giác BB’C vuông tại B’, O là trung điểm của BC nên OB = OC = OB’

Tam giác BC’C vuông tại C’, O là trung điểm của BC nên OB = OC = OC' 

=> OB = OC = OB’= OC’

Do đó, đường tròn tâm O bán kính OB' đi qua B, C, và C'

b) Vì O là trung điểm của BC nên BC = 2 OB = 2R

Xét tam giác OB’C’: B’C’ < OB’ + OC’ = 2R

Do đó, B’C’ < BC

Bài 4 (trang 80): Cho tứ giác ABCD có B = D = 90°.

a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.

b) So sánh độ dài của AC và BD.

Giải rút gọn:

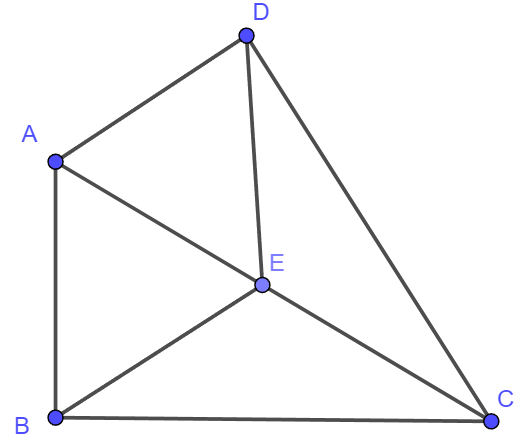
a) Gọi E là trung điểm của AC

Tam giác ADC vuông tại D, E là trung điểm của AC nên EA = EC = ED

Tam giác ABC vuông tại B, E là trung điểm của AC nên EA = OC = EB

=> EA = EC = ED = EB

Do đó 4 điểm A, B, C, D thuộc đường tròn tâm E, đường kính AC

b) Xét đường tròn tâm E:

AC là đường kính

BD là dây cung

=> AC > BD

Bài 5 (trang 80): Cho hai đường tròn (O; 2 cm) và (A; 2 cm) cắt nhau tại C, D, điểm A nằm trên đường tròn tâm O (Hình 20).

a) Vẽ đường tròn (C; 2 cm).

b) Đường tròn (C; 2 cm) có đi qua hai điểm O và A không? Vì sao?

Giải rút gọn:

a)

b) Điểm C nằm trên 2 đường tròn tâm O và tâm A nên: OC = 2cm và AC = 2cm

Bán kính của đường tròn (C; 2cm) là 2 cm nên đường tròn đi qua 2 điểm O và A

Bài 6 (trang 80): Cho hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D, AB = 8 cm. Gọi K, I lần lượt là giao điểm của hai đường tròn đã cho với đoạn thẳng AB (Hình 21).

a) Tính độ dài của các đoạn thẳng CA, CB, DA và DB.

b) Điểm I có phải là trung điểm của đoạn thẳng AB không?

c) Tính độ dài của đoạn thẳng IK.

Giải rút gọn:

a) CA = DA = 6 cm

CB = DB = 4 cm

b) AB = 8; BI = 4 cm 

=> I là trung điểm của đoạn thẳng AB

c) IK = AK - AI = AK - (AB - BI) = 6 - (8 - 4) = 2 cm

Bài 7 (trang 80): Xác định vị trí tương đối của (O; R) và (O'; R') trong mỗi trường hợp sau:

a) OO' = 18; R = 10; R' = 6;

b) OO' = 2; R = 9; R' = 3;

c) OO' = 13; R = 8; R' = 5;

d) OO' = 17; R = 15; R' = 4.

Giải rút gọn:

a) R + R' = 10 + 6 = 16

OO' > R + R’ (18 > 16), nên hai đường tròn này không giao nhau.

b) R - R' = 9 - 3 = 6

OO' < R - R’(2 < 6), nên đường tròn (O;R) đựng đường tròn (O;R’)

c) R + R' = 8 + 5 = 13

OO' = R + R; (13 = 13), nên hai đường tròn này tiếp xúc ngoài.

d) R + R' = 15 + 4 = 19

R - R' = 15 - 4 = 11

R - R’ < OO' < R + R’, nên hai đường tròn này cắt nhau.