BÀI 1. TỌA ĐỘ CỦA VECTƠ

I. TOẠ ĐỘ CỦA MỘT ĐIỂM

II. TOẠ ĐỘ CỦA MỘT VECTƠ 

Bài 1: Tìm tọa độ của các vecto và trong hình 11

Giải nhanh: 

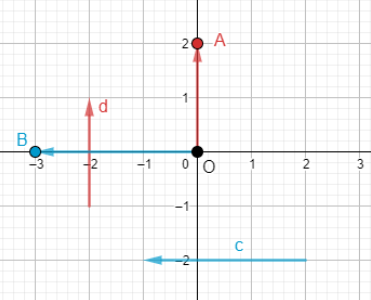
= (2 ; 2); = (- 3 ; 0)

Bài 2: Trong mặt phẳng tọa độ Oxy, cho điểm B(-1,0) và vectơ

a. Biểu diễn vectơ qua hai vectơ và

b. Biểu diễn vectơ qua hai vectơ và

Giải nhanh:

a. .

b. .

III. LIÊN HỆ GIỮA TỌA ĐỘ CỦA ĐIỂM VÀ TỌA ĐỘ VECTƠ

Bài tập 3: Trong mặt phẳng tọa độ Oxy, cho các điểm: A(1,3); B(5,-1); C(2,-2); D(-2,2). Chứng minh

Giải nhanh:

Vậy

BÀI TẬP CUỐI SGK

Bài tập 1: Tìm tọa độ của các vectơ trong Hình 16 và biểu diễn mỗi vectơ đó qua hai vectơ

Giải nhanh:

+ Vẽ

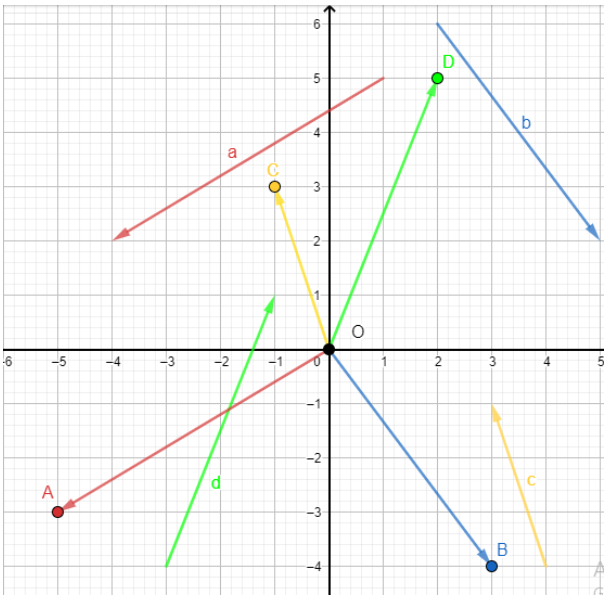
=> Tọa độ của A (-5; -3), B (3; -4), C (-1; 3), D (2; 5)

Vì nên

nên

nên

nên

Bài tập 2: Tìm tọa độ của các vectơ sau:

.

b.

c. - 4

d. 0,5 +

Giải nhanh:

.

b.

c.

d.

Bài tập 3: Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:

a.

b.

Giải nhanh:

a. thì

b. thì  

Bài tập 4: Trong mặt phẳng toạ độ Oxy cho ba điểm A(2,3); B(-1,1); C(3,-1)

a. Tìm tọa độ điểm M sao cho

b. Tìm toạ độ trung điểm N của đoạn thẳng AC. Chứng minh

Giải nhanh:

a. Gọi M (a ; b)

Để thì M (6 ; 1)

b. Gọi N (x ; y) và

Do N là trung điểm AC nên

N

Ta có: và  

Vậy

Bài tập 5: Trong mặt phẳng toạ độ Oxy, cho điểm M(−1;3)

a. Tìm toạ độ điểm A đối xứng với điểm M qua gốc O

b. Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox

c. Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy

Giải nhanh:

a. A (1; -3). 

b. B (-1; -3)

c. C (1 ; 3)

Bài tập 6: Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(−3;1),B(−1;3), I(4;2). Tìm toạ độ của hai điểm C,D sao cho tứ giác ABCD là hình bình hành nhận I làm tâm đối xứng.

Giải nhanh:

Gọi C (a; b), D (c; d) và  

Do I là trung điểm AC và BD và

Ta có: và

Do

Bài tập 7: Trong mặt phẳng toạ độ Oxy, cho tam giác ABC. Các điểm M(1;−2),N(4;−1) và P(6;2) lần lượt là trung điểm của các cạnh BC,CA,AB. Tìm tọa độ của các điểm A,B,C

Giải nhanh:

Theo tính chất đường trung bình trong một tam giác ta có:

và

Gọi A (a₁ ; a₂), B (b₁ ; b₂), C (c₁ ; c₂)

Ta có : , , .