BÀI 4. VỊ TRÍ TƯƠNG ĐỐI VÀ GÓC GIỮA HAI ĐƯỜNG THẲNG. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG

I. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG

Bài 1: Xét vị trí tương đối của hai đường thẳng

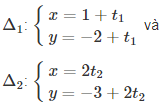
Giải nhanh:

.2 đường thẳng và trùng nhau

Bài 2: Xét vị trí tương đối của hai đường thẳng d: x + 2y -2 = 0 với mỗi đường thẳng sau

Δ1: 3x-2y + 6 =0

Δ2: x + 2y + 2 = 0

Δ3: 2x + 4y - 4 = 0

Giải nhanh:

d và cắt nhau tại một điểm duy nhất

d và song song với nhau

d và trùng nhau

II. GÓC GIỮA HAI ĐƯỜNG THẲNG

Bài 1: Tính số đo góc giữa hai đường thẳng trong mỗi trường hợp sau:

: x = -3 + t và y = 2 + 3t

: y - 2 = 0

b. : 2x - y = 0 và : -x + 3y - 5 = 0

Giải nhanh:

a. Đường thẳng lần lượt có vectơ chỉ phương = (3; 3);

cos( =

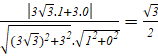
Vậy (

b. Đường thẳng lần lượt có vectơ pháp tuyến = (2; -1);

cos( =

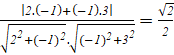
Vậy (

III. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG

Bài 1: a. Tính khoảng cách từ điểm O(0;0) đến đường thẳng

b. Tính khoảng cách giữa hai đường thẳng song song:

: x - y + 1 = 0

: x - y + 1 = 0

Giải nhanh:

a. Ta có:

D (O; ) =

b. Lấy M(0; 1)

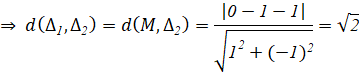
BÀI TẬP CUỐI SGK 

Bài tập 1: Xét vị trí tương đối của mỗi cặp đường thẳng sau:

a. d1:

b.

c. d5: 4x + 2y -3 = 0 và d6: x = và y =

Giải nhanh:

a. Toạ độ giao điểm của hai đường thẳng d₁, d₂ là nghiệm của hệ phương trình:

Hệ phương trình có nghiệm duy nhất nên 2 đường thẳng cắt nhau.

b. Toạ độ giao điểm của hai đường thẳng d₃, d₄ là nghiệm của hệ phương trình:

=> Vô nghiệm

=> Hai đường thẳng song song với nhau 

c. Toạ độ giao điểm của hai đường thẳng d₅, d₆ tương ứng với t thoả mãn phương trình:

4 => Vô số nghiệm 

=> 2 đường thẳng trùng nhau

Bài tập 2: Tính số đo góc giữa hai đường thẳng d1: 2x -y + 5 = 0 và d2: x-3y+3=0

Giải nhanh:

Ta có: ;

Cos (d₁, d₂) =

=> (d₁, d₂) = 45^o

Bài tập 3: Tính khoảng cách từ một điểm đến một đường thẳng trong mỗi trường hợp sau:

a. A(1; -2) và

b. B(-3; 2) và

Giải nhanh:

a. A(1; -2) và

d(A, ) =

b. B(-3; 2) và

PTTQ : 2x + y + 3 = 0

d(B, ) =

Bài tập 4: Với giá trị nào của tham số m thì hai đường thẳng sau đây vuông góc?

: mx - y + 1 = 0

: 2x - y + 3 = 0

Giải nhanh:

Đường thẳng :

Đường thẳng :

Ta có: 

Vậy m = - thì hai đường thẳng và vuông góc với nhau. 

Bài tập 5:Cho ba điểm A(2;-1); B(1;2) và C(4; -2). Tính số đo góc BAC và góc giữa hai đường thẳng AB; AC

Giải nhanh:

Ta có:

cos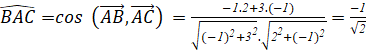

cos (AB, AC) =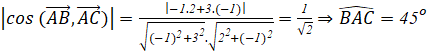

Bài tập 6: Cho ba điểm A(2;4); B(-1;2) và C(3;-1). Viết phương trình đường thẳng đi qua B đồng thời cách đều A và C

Giải nhanh:

Gọi d là đường thẳng đi qua B và có vectơ pháp tuyến là

Vậy phương trình d là:

a(x + 1) + b(y – 2) = 0 ax + by + (a – 2b) = 0

Ta có: 

d(A, d) = d(C, d)

TH1: Chọn b = 1, a = 5, phương trình đường thẳng d là: 

5x + y + 5 -2 = 0 hay 5x + y + 3  = 0

TH2: Chọn a = 1, b = 7, phương trình đường thẳng d là: 

x + 7y + 1 – 2.7 = 0 hay x + 7y – 13 = 0 

Vậy phương trình đường thẳng cần lập là 5x + y + 3 = 0 hoặc x + 7y – 13 = 0.

Bài tập 7: Có hai  con tàu A và B cùng xuất phát từ hai bến, chuyển động đều theo đường thẳng ngoài biển. Trên màn hình ra đa của trạm điều  khiển (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki - lô - mét), sau khi xuất phát t (giờ) (t≥0), vị trí của tàu A có tọa độ được xác định bởi công thức: 

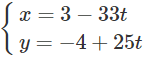
vị trí của tàu B có tọa độ là (4-30t;3-40t)

a.  Tính cosin góc giữa hai đường đi của hai tàu A và B.

b. Sau bao lâu kể từ thời điểm xuất phát hai tàu gần nhất?

c. Nếu tàu A đứng yên ở vị trí ban đầu, tàu B chạy thì khoảng cách ngắn nhất giữa hai tàu bằng bao nhiêu?

Giải nhanh:

a. Tàu A di chuyển theo hướng vectơ

Tàu B di chuyển theo hướng vectơ

Gọi là góc giữa hai đường đi của hai tàu, ta có:

cos =

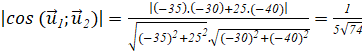
b. Sau t giờ, vị trí của tàu A là điểm M có tọa độ là: M(3 – 35t ; - 4 + 25t)

Sau t giờ, vị trí của tàu B là điểm N có toạ độ là: N(4 – 30t ; 3 – 40t)

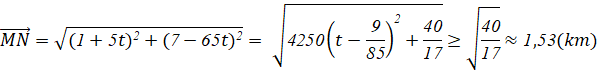
MN nhỏ nhất xấp xỉ 1,53 km khi t =